一、选择题
(本题共 8 小题, 每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有一项符合题目要 求,把所选项前的字母填在题后的括号内. )
(1)
曲线 y=x2−1x2+x 的渐近线的条数为 ()
(A) 0 .
(B) 1 .
(C) 2 .
(D) 3 .
(1)
(2)
设函数 f(x)=(ex−1)(e2x−2)⋯(enx−n), 其中 n 为正整数, 则 f′(0)=()(A) (−1)n−1(n−1) !.
(B) (−1)n(n−1) !
(C) (−1)n−1n !
(D) (−1)nn!.
(2)
解答分析
- 第一步:理解题目
- 小总结:需要计算多项乘积函数在某一点的导数。
- 将x=0代入,第一项e0−1=0, - 则全部为0,得到f(0)=0- 第二步:应用导数定义
- 小总结:使用导数的定义,计算 f′(0)。
- 计算步骤
- 导数定义:f′(0)=x→0limxf(x)−f(0)。
- 代入 f(x):f′(0)=x→0limx(ex−1)(e2x−2)⋯(enx−n)−0。
- 第三步:化简表达式
- 小总结:将每个项分别展开并计算极限。
- 计算步骤
- 对于分子的第一项,将其和分母x进行等价:limx→0xex−1=1 2. 将x=0代入剩余各项:e2×0−2=1−2=−1,ek×0−k=1−k=−(n−1)(对于 k=2,…,n)。
- 计算乘积的极限:
- 每一项都是负的,除去第一项为1,还有n−1项,因此,(−1)n−1
- 当 x→0,得到 f′(0)=(−1)n−1(n−1)!。
- 结论
- 整体思路的总结:
- 利用导数的定义来计算 f′(0)。
- 将每个项在 x→0 时分别展开并计算极限。
- 根据以上分析,正确答案是 (A) (−1)n−1(n−1)!。
答 应选 (A).
(3)
如果函数 f(x,y) 在点 (0,0) 处连续, 那么下列命题正确的是 ()
(A) 若极限 x→0y→0lim∣x∣+∣y∣f(x,y) 存在, 则 f(x,y) 在点 (0,0) 处可微.
(B) 若极限 x→0y→0limx2+y2f(x,y) 存在, 则 f(x,y) 在点 (0,0) 处可微.
(C) 若 f(x,y) 在点 (0,0) 处可微,则极限 x→0y→0lim∣x∣+∣y∣f(x,y) 存在.
(D) 若 f(x,y) 在点 (0,0) 处可微, 则极限 x→0y→0limx2+y2f(x,y) 存在.
(3)
答 应选(B).
分析 本题主要考查二元函数可微的概念和性质。
- (1)可微的充分必要条件 : 函数 z=f(x,y) 在点 (x0,y0) 处可微,等价于$$\displaystyle \lim _{(x, y) \rightarrow\left(x_0, y_0\right)} \frac{f(x, y)-f\left(x_0, y_0\right)-f_x^{\prime}\left(x_0, y_0\right)\left(x-x_0\right)-f_y^{\prime}\left(x_0, y_0\right)\left(y-y_0\right)}{\sqrt{\left(x-x_0\right)2+\left(y-y_0\right)2}}=0 .$$
- (2)可微的必要条件 : 若函数 z=f(x,y) 在点 (x,y) 处可微,则该函数在点 (x,y) 处的偏导数 ∂x∂z,∂y∂z 都存在.
A:令f(x,y)=∣x∣+∣y∣
- fx′(0,0)=x→0limx−0f(x,0)−f(0,0)=x→0limx∣x∣
- 偏导数不存在,一定不可微
B:要证 f(x,y) 在点 (0,0) 处可微, 可$$\displaystyle \lim _{(x, y) \rightarrow(0,0)} \frac{f(x, y)-f(0,0)-f_x{\prime}(0,0)(x-0)-f_y{\prime}(0,0)(y-0)}{\sqrt{(x-0)2+(y-0)2}}=0 .$$
- f(0,0)=(x,y)→(0,0)limf(x,y)
- =(x,y)→(0,0)lim[x2+y2f(x,y)⋅(x2+y2)]
- =(x,y)→(0,0)limx2+y2f(x,y)⋅(x,y)→(0,0)lim(x2+y2)=0.
- fx′(0,0)=x→0limx=0f(x,0)−f(0,0)=x→∞limxf(x,0)=x→0lim(x+02f(x,0)⋅x)
- =x→0limx→02f(x,0).x→0limx=0.
- 同理:fy′(0,0)=0
- (x,y)→(0,0)limx2+y2f(x,y)−0−0⋅x−0⋅y
- =(x,y)→(0,0)lim[x2+y2f(x,y)⋅x2+y2]
- =(x,y)→(0,0)limx2+y2f(x,y)⋅(x,y)→(0,0)limx2+y2=0.
对于C,D选项,取函数 f(x,y)=1,
- 则当x,y趋向于0时,分子为常数,分母为0,则极限都是无穷大
- x→0y→0lim∣x∣+∣y∣f(x,y) 和x→0y→0limx2+y2f(x,y)都不存在
(4)
设 Ik=∫0kπex2sinx dx(k=1,2,3), 则有 ()
(A) I1<I2<I3.
(B) I3<I2<I1.
(C) I2<I3<I1.
(D) I2<I1<I3.
(4)
解
这个数学题目,我们可以构建一个二叉树形式的解答过程:
- 将 ex2sinx 折成 ex2与sinx
- 比较sinx:∣>0∫0πsinxdx∣=∣<0∫π2πsinxdx∣=>0∫2π3πsinxdx∣
- 比较ex2:0<∫0πex2dx<∫π2πex2dx<∫2π3πex2dx
- 以上两项相乘:<0∫π2πexsinxdx<∫0πex2sinxdx<∫2π3πex2sinxdx
- 问题: 比较 I1,I2,I3 的大小
- 第一步:比较 I1 和 I2
- 计算 I2:
- 分解: I2=∫02πex2sinxdx分区间I1+<0∫π2πex2sinxdx
- 结论: I2<I1
- 第二步:比较 I2 和 I3(这一步可以省略,直接进行第三步)
- 计算 I3:
- 分区间: I3=I2+>0∫2π3πex2sinxdx
- 结论: I3>I2
- 第三步:比较 I1 和 I3
- 比较: I3=I1+>0∫π2πex2sinxdx+∫2π3πex2sinxdx
- 分析第二部分: ∣<0∫π2πex2sinxdx∣<∣>0∫2π3πex2sinxdx∣
- 结论: I3>I1
- 最终结论: I3>I1>I2(选择 (D)
(5)
设 α1=00c1,α2=01c2,α3=1−1c3,α4=−11c4, 其中 c1,c2,c3,c4 为任意常数, 则下列向量组线性相关的为 ()(A) α1,α2,α3.
(B) α1,α2,α4.
(C) α1,α3,α4.
(D) α2,α3,α4.
(5)
答 应选(C).
解 首先, 当 c1=1 时,行列式
- ∣α1,α2,α3∣=−1,∣α1,α2,α4∣=1,此时向量组 α1,α2,α3 与 α1,α2,α4 都线性无关, 即选项 (A) 与 (B) 排除.
其次, 当 c2=0,c3=c4=1 时, 行列式 ∣α2,α3,α4∣=−2, 即此时向量组 α2,α3,α4 也是线性无关的, 选项 (D)也排除,故选(C).
事实上,当 c1=0 时, 由于 α1 为零向量, 故 α1,α3,α1 线性相关; 当 c1=0 时, 有 - (c3+c4)α1−c1(α3+α4)=0,所以对任意的常数 c1,c3,c4 而言, α1,α3,α4 都是线性相关的. 这证明了应该选 (C).
注 也可以考查行列式 ∣α1,α3,α4∣ 是否为零.
(6)
设 A 为 3 阶矩阵, P 为 3 阶可逆矩阵, 且 P−1AP=100010002. 若 P=(α1,α2,α3), Q=(α1+α2,α2,α3), 则 Q−1AQ=()(A) 100020001.
(B) 100010002.
(C) 200010002.
(D) 200020001.
(6)
答 应选(B).
解法 1 由题设 P−1AP=100010002 知, 矩阵 A 是可相似对角化的矩阵,因而其相似变换矩阵 P 的列 向量 α1,α2,α3 是 A 的分别属于特征值 λ1=1,λ2=1,λ3=2 的特征向晝. 由于 λ1=λ2=1 是 A 的 2 重特征值, 因此 α1+α2 仍是 A 的属于特征值 1 的特征向量, 即 A(α1+α2)=1⋅(α1+α2), 从而有
- Q−1AQ=100010002. 应选(B).
解法 2 因为矩阵 Q 是对矩阵 P 作的一次初等列变换, 即将 P 的第 2 列加到第 1 列上得到的, 所以有Q=P110010001从而有 - Q−1AQ=110010001−1P−1AP110010001=1−10010001100010002110010001=100010002,即选项 (B) 是正确的.
(7)
设随机变量 X 与 Y 相互独立, 且分别服从参数为 1 与参数为 4 的指数分布, 则 P{X<Y}=()
(A) 51.
(B) 31.
(C) 32.
(D) 54.
(7)
解
由于 X 和 Y 相互独立,所以他们的联合概率密度函数为 fX(x) 和 fY(y) 的乘积
f(x,y)=fX(x)fY(y)
- 定义随机变量 X 和 Y 的概率密度函数
- X 的概率密度函数:fX(x)={e−x,0,x>0其他
- Y 的概率密度函数:fY(y)={4e−4y,0,y>0其他
- 独立则f(x,y)=fX(x)fY(y)={4e−x−4y,0,x>0,y>0其他
计算 P{X<Y}
答案是 (A) 51。
答 应选 (A).
解 由已知得, X 与 Y 的概率密度分别为
- fX(x)={e−x,0,x>0, 其他, fY(y)={4e−4y,0,y>0, 其他, 又 X 与 Y 相互独立, 所以 X 与 Y 的联合概率密度为
- f(x,y)=fX(x)fY(y)={4e−x−4y,0,x>0,y>0, 其他, 故
- P{X<Y}=∬x<yf(x,y)dx dy=4∫0+∞e−x dx∫x+∞e−4y dy=51.
(8)
将长度为 1 m 的木棒随机地截成两段, 则两段长度的相关系数为 ( )
(A) 1 .
(B) 21.
(C) −21.
(D) -1 .
(8)
解
应选(D).
- 设两段长度分别为 X,Y, 则 X+Y=1,
- 即 Y=1−XY=aX+bρXY=−1
- 所以 X 与 Y 存在线性关系, 且为负相关,故选(D).
二、填空题
(本题共 6 小题, 每小题 4 分, 共 24 分, 把答案填在题中横线上. )
(9)
若函数 f(x) 满足方程 f′′(x)+f′(x)−2f(x)=0 及 f′′(x)+f(x)=2ex, 则 f(x)=
(9)
答 应填 ex.
- 解法 1 (用特征方程求解)
- 先计算齐次方程的通解
微分方程 f′′(x)+f′(x)−2f(x)=0 的 - 特征方程为 r2+r−2=0因式分解(r+2)(r−1)=0.
- 特征根为 r1=1,r2=−2,
- 其通解为 f(x)=C1ex+C2e−2x.
- f′(x)=C1ex−2C2e−2x
- f′′(x)=C1ex+4C2e−2x
- 将齐次的解代入非齐次方程
将 f(x)和f′′(x)代入方程 f′′(x)+f(x)=2ex, 得 - 代入C1ex+4C2e−2x+C1ex+C2e−2x
- 整理2C1ex+5C2e−2x=2ex,
- 对比同类项系数,所以 C1=1,C2=0,
- 故 f(x)=ex.
- 解法 2 (加减消去二阶导)
- 由 {f′′(x)+f′(x)−2f(x)=0f′′(x)+f(x)=2ex,得f′(x)−3f(x)=−2ex.
- 此一阶非齐次线性微分方程的通解为
f(x)=e3x[C+∫(−2ex)e−3x dx]=ex+Ce3x,- 求C
- 将 f(x)=ex+Ce3x,f′′(x)=ex+9Ce3x 代人方程 f′′(x)+f(x)=2ex,
- 得 2ex+10Ce3x=2ex,所以 C=0,
- 故 f(x)=ex.
| 特征方程 λ2+pλ+q=0 的根 | 微分方程 y′′+py′+qy=0 的通解 |
|---|
| 两个不相等的实根 λ1,λ2 | y=C1eλ1x+C2eλ2x |
| 两个相等的实根 λ1=λ2 | y=(C1+C2x)eλ1x |
| 对共轭复根 λ1,2=α±βi | y=eαx(C1cosβx+C2sinβx) |
(10)
∫02x2x−x2 dx=
(10)
计算定积分 ∫02x2x−x2dx
- 观察被积函数 x2x−x2 ,因为同时含有x与x2
- 可以进行配方: 2x−x2 重写为 1−(x−1)2
- 积分变为 ∫02x1−(x−1)2dx
- 根号下有单独的x²,而不是同时含有x与x2,则用三角代换
- 令 x−1=sint, 则 x=1+sint,dx=costdt
- 换限:∫022−1=sint0−1=sint{ 上限: t=2π 下限: t=−2π
- 三角代换得:∫−2π2π(1+sint)1−sint2costdt1−sint2=cost∫−2π2π(1+sint)⋅cost⋅costdt
- 将加号左右两项拆开:=偶函数翻倍=2∫02πcos2tdt∫−2π2πcos2tdt+区间对称,奇函数sint=0∫−2π2πsint⋅cos2tdt
- =2∫02πcos2tdt华里士公式2⋅21×1×2π=2π
- 合并整理得: 2π
2000 年数一试题
∫012x−x2 dx=
2007 年数一试题
∫12x31ex1 dx=
2015 年数一试题
∫−2π2π(1+cosxsinx+∣x∣)dx=
(11)
grad(xy+yz)(2,1,1)=
(11)
答 应填 i+j+k.
- 梯度的定义
- 函数 u=f(x,y,z) 在点 (x0,y0,z0) 处的梯度为
gradf(x0,y0,z0)=fx′(x0,y0,z0)i+fy′(x0,y0,z0)j+fz′(x0,y0,z0)k
- 令 f(x,y,z)=xy+yz,
- 则 ∂x∂f=y,∂y∂f=x−y2z,∂z∂f=y1
- 所以 ∂x∂f(2,1,1)=1,∂y∂f(2.1,1)=1,∂z∂f(2.1,1)=1,
- grad(xy+yz)(2,1,1)=i+j+k.
(12)
设 Σ={(x,y,z)∣x+y+z=1,x⩾0,y⩾0,z⩾0}, 则 ∬Σy2 dS=
(12)
答 应填 123.
- 转换投影是对积分区域转换投影,还是对被积函数转换投影?
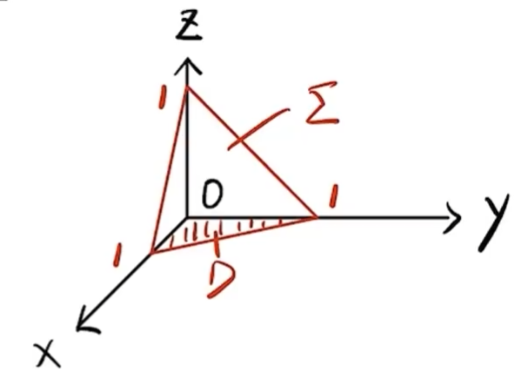 ,积分区域投影后,
,积分区域投影后,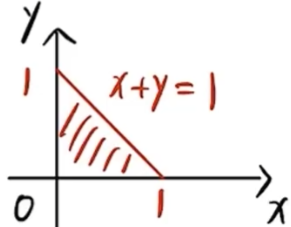
- 要投影的方程:z=1−x−y
- 解 记 D={(x,y)∣x+y⩽1,x⩾0,y⩾0}, 则
- ∬Σy2 dS=
- =∬Dy23zx2+zy2+1dxdy
- =3∫Dy2dxdy
- 后积先定限限内穿条线3∫01dy∫01−yy2dx
- =3∫01(y2−y3)dy
- 牛莱3(3y3−4y4)01=3⋅121=123
(13)
设 α 为 3 维单位列向量, E 为 3 阶单位矩阵,则矩阵 E−ααT 的秩为
(13)
答 应填 2 .
解 令 B=ααT,α 是 3 维单位列向量, BT=B, 则 B 是秩为 1 的实对称矩阵,故 B 能相似对角化, B 的 特征值是 αTα,0,0, 即 1,0,0, 则 E−ααT=E−B 也可相似对角化且特征值是 0,1,1. 于是 r(E−ααT)=2.
注 (1) 秩为 1 的 n 阶方阵特征值是 \displaystyle \sum_{i=1}^n a_{i ̈} (迹), 0 ( n−1 重).
(2)
能相似对角化的矩阵的秩等于其非零特征值的个数 (考虑重数).
(3)
对于填空题, 当然还可以取一个具体的 α 去求解, 如取 α=100.
(14)
设 A,B,C 是随机事件, A 与 C 互不相容, P(AB)=21,P(C)=31, 则 P(AB∣Cˉ)=
(14)
解
我们需要考虑事件 A,B,C 之间的关系以及条件概率的计算。此问题涉及到条件概率 P(AB∣Cˉ) 的求解
- 确定P(AB∣Cˉ)=P(Cˉ)P(ABCˉ)
- 计算 P(Cˉ):P(Cˉ)=1−P(C)=1−31
- 确定 P(ABCˉ):P(ABCˉ)=P(AB)−P(ABC)=21−0
- 求P(ABC):因为A 和 C 互不相容(互斥),得P(AC)=0,P(ABC)=0
- 计算P(AB∣Cˉ)=P(Cˉ)P(ABCˉ)=1−3121=43
通过这个二叉树,我们可以看到,由于 A 和 C 互不相容,这影响了 P(ABC) 的值,进而影响 P(ABCˉ)。最终得出的结论是 P(AB∣Cˉ)=43,与答案相符。
答 应填 43.
解 因为 A 与 C 互不相容, 所以 P(AC)=0. 又 ABC⊂AC, 所以 P(ABC)=0, 故
- P(AB∣Cˉ)=P(Cˉ)P(ABCˉ)=1−P(C)P(AB)−P(ABC)=1−1/31/2=43.注 AC=∅, 则 ABC=∅B=∅, 同样得到 P(ABC)=0.
三、解答题
( 本题共 9 小题, 共 94 分,解答应写出文字说明、证明过程或演算步骤. )
(15)
(本题满分 10 分)
证明 xln1−x1+x+cosx⩾1+2x2(−1<x<1).
(15)
解法分析
- 证法 2:使用二阶导数
- 定义函数:f(x)=xln1−x1+x+cosx−1−2x2。
- 证明:
- 求一阶和二阶导数:
- 求f′(x)
- (xln1−x1+x)′=ln1−x1+x+x(ln1−x1+x)′
- =ln1−x1+x+x1−x1+x1(1−x)2(1−x)+(1+x)
- =ln1−x1+x+1−x22x.
- f′(x)=ln1−x1+x+1−x22x−sinx−x 2. 求 f′′(x)
1. - (ln1−x1+x)′=[ln(1+x)−ln(1−x)]′=1−x22.
- (1−x22x)′=(1−x2)22(1−x2)+2x⋅2x=(1−x2)22(1+x2)
- f′′(x)=(1−x2)24−1−cosx 2. 分析二阶导数:f′′(x)=(1−x2)24−1−cosx≥0,因为 (1−x2)24≥4 且 1+cosx≤2,4−2≥2≥0 3. 因为f′′(x)≥0, f′(0)=0意味着
- 当 −1<x<0 时, f′(x)<0;
- 当 0<x<1 时, f′(x)>0, 3. 0点是极小值 4. 得知f(x) 在 (−1,1) 上是凹的
- 因为 f(0)=0 , 1. 当 −1<x<0 时, f′(x)<0 2. 当 0<x<1 时, f′(x)>0 3. 则对所有 −1<x<1 ,f(x)≥0 成立
结论
根据以上两种方法的分析,不等式 xln1−x1+x+cosx⩾1+2x2 对所有 −1<x<1 成立。
了解了,我将遵循您的指示,详细展开计算步骤,并确保每个步骤正确地反映其父子关系:
- 定义函数
- f(x)=xln1−x1+x+cosx−1−2x2
- 求一阶导数 f′(x)
- 计算 (xln1−x1+x)′
- 使用乘法法则:u′v+uv′
- u=x,u′=1
- v=ln1−x1+x,v′=(ln1−x1+x)′
- 计算 (ln1−x1+x)′
- 使用链式法则:dxd[lnu]=u1⋅u′
- u=1−x1+x,u′=(1−x1+x)′
- 计算 (1−x1+x)′
- 得 (1−x)22
- 故 (ln1−x1+x)′=1−x22
- 合并得 f′(x)=ln1−x1+x+1−x22x−sinx−x
- 求二阶导数 f′′(x)
- 对 f′(x) 再次求导
- 计算 (ln1−x1+x)′′
- 再次使用链式法则:(1−x22)′
- 得 (1−x2)24x
- 计算 (1−x22x)′
- 使用乘法法则:u′v+uv′
- u=2x,u′=2
- v=(1−x2)1,v′=(1−x21)′
- 计算 (1−x21)′
- 得 (1−x2)22x
- 故 (1−x22x)′=1−x22+(1−x2)24x2
- 合并得 f′′(x)=(1−x2)24−1−cosx
- 分析二阶导数 f′′(x)
- f′′(x)=(1−x2)24−1−cosx≥0
- 因为 (1−x2)24≥4 且 1+cosx≤2
- 根据 f′′(x) 的性质分析 f(x)
- f(x) 在 (−1,1) 上是凹的
- f′(0)=0
- 当 −1<x<0 时, f′(x)<0
- 当 0<x<1 时, f′(x)>0
- f(0)=0,故 f(x)≥0 对所有 −1<x<1 成立
通过这种结构化的展
证法 1 记 f(x)=xln1−x1+x+cosx−1−2x2(−1<x<1), 则 f(x) 为偶函数.
当 0⩽x<1 时,f′(x)=ln1−x1+x+1−x2x(1+x2)−sinx⩾ln1−x1+x+(x−sinx)⩾0,因为 f(0)=0, 所以 f(x)⩾0(0⩽x<1).
由于 f(x) 为偶函数, 所以 f(x)⩾0(−1<x<1), 即
- xln1−x1+x+cosx⩾1+2x2(−1<x<1).证法 2 记 f(x)=xln1−x1+x+cosx−1−2x2(−1<x<1), 则
- f′(x)=ln1−x1+x+1−x22x−sinx−x,
- f′′(x)=(1−x2)24−1−cosx.当 −1<x<1 时, 由于 (1−x2)24⩾4,1+cosx⩽2, 所以 f′′(x)⩾2>0, 从而 f′(x) 单调增加.
又因为 f′(0)=0, 所以当 −1<x<0 时, f′(x)<0; 当 0<x<1 时, f′(x)>0. 故 f(0) 是 f(x) 在区间 (−1,1) 内的最小值. 因为 f(0)=0, 所以 - f(x)⩾0(−1<x<1), 即 xln1−x1+x+cosx⩾1+2x2(−1<x<1).
(16)
(本题满分 10 分)
求函数 f(x,y)=xe−2x2+y2 的极值.
(16)
解
该问题涉及求函数 f(x,y)=xe−2x2+y2 的极值。
求函数 f(x,y) 的一阶偏导数 fx′(x,y) 和 fy′(x,y)。
- fx′(x,y)==0(1−x2)=0e−2x2+y2
- fy′(x,y)==0−xy=0e−2x2+y2
- 求驻点
- 令 fx′(x,y)=0 和 fy′(x,y)=0,解得驻点 (1,0) 和 (−1,0)。
求函数 f(x,y) 在驻点的二阶偏导数(全部乘法求导,除法也转换成乘法求导)
- fx′(x,y) 对x求偏导,A=fxx′′(x,y)一个不动另一个求导−2xe−2x2+y2+(1−x2)e−2x2+y2(−x)=(x3−3x)e−2x2+y2
- fx′(x,y) 对y求偏导,B=fxy′′(x,y)=y(x2−1)e−2x2+y2
- fy′(x,y)对y求偏导,C=fyy′′(x,y)=(−x+xy2)⋅e−2x2+y2
判断极值类型
- 在点 (1,0),计算 AC−B2 和 A 的值
- 当x=1:y=0 时, ∴A=−2e−21:B=0:C=−e−21
- AC−B2>0
- A<0
- f(x,y)则在点 (1,0) 处为极大值,f(1,0)=e−21
- 在点 (−1,0),计算 AC−B2 和 A 的值
- A=2e−21,B=0,C=e−21
- 由于 AC−B2>0
- 且 A>0
- f(x,y) 在点 (−1,0) 处取极小值 f(−1,0)=−e−21
通过以上步骤,我们可以看到如何从函数的定义开始,逐步求出其一阶偏导数,确定驻点,计算二阶偏导数,使用二阶导数判别法确定极值的类型,并计算出极值。
由 f(x,y)=xe−2x′+y′, 得
- ∂x∂f(x,y)=(1−x2)e−2x2+y2,∂y∂f(x,y)=−xye−2x2+y2,令 {∂x∂f(x,y)=0,∂y∂f(x,y)=0, 解得驻点 (1,0),(−1,0). 记
- A=∂x2∂2f(x,y)=x(x2−3)e−2x′+y′,B=∂x∂y∂2f(x,y)=y(x2−1)e−2x2+y2,
- C=∂y2∂2f(x,y)=x(y2−1)e−2t2+y′,在点 (1,0) 处, 由于 AC−B2=e2>0,A=−e2<0, 因此 f(1,0)=e1 为 f(x,y) 的极大值; 在点 (−1,0) 处, 由于 AC−B2=e2>0,A=e2>0, 因此 f(−1,0)=−e1 为 f(x,y) 的极小值.
注 二元函数求无条件极值, 做法是先用必要条件找出可能的极值点,再用充分判别法去判定,这里 有一定的运算量. 不论是显函数还是隐函数求二元函数无条件极值, 这都是基本要求,读者一定要熟练 等握.
(17)
(本题满分 10 分)
求幂级数 n=0∑∞2n+14n2+4n+3x2n 的收玫域及和函数.
(17)
解法 1un(x)=2n+14n2+4n+3x2n,n→∞limun(x)un+1(x)=x2,当 x2<1, 即 ∣x∣<1 时, 原级数收玫, 当 x2>1, 即 ∣x∣>1 时, 原级数发散.
所以界级数 n=0∑∞2n+14n2+4n+3x2n 的收敛半径 R=1 (注意该慗级数是缺项军级数).
又因为当 x=±1 时,级数 n=0∑∞2n+14n2+4n+3 发散, 所以军级数 n=0∑∞2n+14n2+4n+3x2n 的收玫域为 (−1,1).
记 S(x)=n=0∑∞2n+14n2+4n+3x2n(−1<x<1), 则
- S(x)=n=0∑∞(2n+1)x2n+2n=0∑∞2n+11x2n.由于
- n=0∑∞(2n+1)x2n=(n=0∑∞x2n+1)′=(1−x2x)′=(1−x2)21+x2(−1<x<1),
- n=0∑∞2n+1x2n=x1n=0∑∞2n+1x2n+1=x1∫0x(n=0∑∞t2n)dt
- =x1∫0x1−t21 dt=2x1ln1−x1+x(0<∣x∣<1),且 S(0)=3, 所以
- S(x)={(1−x2)21+x2+x1ln1−x1+x,3,0<∣x∣<1,x=0.解法 2 求收敛域同解法 1. 记 S(x)=n=0∑m2n+14n2+4n+3x2n(−1<x<1), 则
- S(x)=x1n=0∑∞2n+14n2+4n+3x2n+1=x1∫0x[n=0∑∞(4n2+4n+3)t2n]dt(0<∣x∣<1).因为
- n=0∑∞3x2n=1−x23(∣x∣<1),
- n=1∑∞4nx2n=2x(n=1∑∞x2n)′=2x(1−x2x2)′=(1−x2)24x2(∣x∣<1),
- n=1∑∞4n2x2n=x(n=1∑∞2nx2n)′=x[x(n=1∑∞x2n)′]′
- =x[x(1−x2x2)′]′=x[(1−x2)22x2]′=(1−x2)34x2(1+x2)(∣x∣<1),所以
- S(x)=x1∫0x(1−t2)33+2t2+3t4 dt=(1−x2)21+x2+x1ln1−x1+x(0<∣x∣<1).又因为 S(0)=3, 所以
- S(x)={(1−x2)21+x2+x1ln1−x1+x,3,0<∣x∣<1,x=0.
(18)
已知曲线 L:{x=f(t),y=cost(0⩽t<2π), 其中函数 f(t) 具有连续导数, 且 f(0)=0, f′(t)>0(0<t<2π). 若曲线 L 的切线与 x 轴的交点到切点的距离恒为 1 , 求 函数 f(t) 的表达式, 并求以曲线 L 及 x 轴 和 y 轴为边界的区域的面积.
(18)
(1)
切线斜率 k=yx′=xt′yt′=f′(t)−sint,
- 有点斜式,求得切线方程为y−cost=−f′(t)sint(x−f(t)).
求这条切线与x轴的交点
- 令 y=0, 得 x0=f′(t)sintcost+f(t).
- 有交点(x0,y0)到曲线L上的切点(f(t),cost)的距离为1,即[f′(t)sintcost]2+cos2t=1
- 利用1−cos2t=sin2t化简,得f′(t)=costsin2t=cost1−cost.
(2) 由于对f′(t)积分得,f(t)=ln(sect+tant)−sint
- 因为0≤t≤2π,则要求出 f(0)=0,t→2πlimf(t)=+∞
- 得出积分区域0≤x<+∞,0≤y≤1
用的大学里面的数学公式,而并非二重积分。
- 求面积与求体积,
- 二重积分的积分区域相同
- 被积函数不同求
- 求面积为对常数1积分
- 求体积为对点到直线的距离r=A2+B2∣Ax+By+C∣积分,2πr
- 求面积
- s=∫01dσ=∫0+∞dx∫0f(x)1dy
S=∫0+∞ydx=∫02πcost⋅f′(t)dt=∫02π(1−cos2t)dt=∫02πsin2tdt=4π
- 求体积
- ∫∫ydσ=2π∫0+∞dx∫0f(x)ydy
Vx=π∫0+∞y2dx=π∫02πcos2t⋅f′(t)dt=π∫02πsin2tcostdt=π0∫2πsin2tdsint=3π - 能否用二重积分计算,涉及到二重积分如何算参数方程
- 先写出S=∫0+∞ydx,然后分别将y和dx对t的参数方程代入进去
(19)
(本题满分 10 分)
已知 L 是第一象限中从点 (0,0) 沿圆周 x2+y2=2x 到点 (2,0), 再沿圆周 x2+y2=4 到点 (0,2) 的曲线段,计算曲线积分 I=∫L3x2y dx+(x3+x−2y)dy.
(19)
本题主要考查第二类曲线积分的计算. 可以补线段成为一个闭曲线后再利用格林公式.
- 格林公式
设闭区域 D 由分段光滑的曲线 L 围成, 若函数 P(x,y) 及 Q(x,y) 在 D 上具有一阶连续偏导数, 则有
∮LP dx+Q dy=∬D(∂x∂Q−∂y∂P)dx dy- 其中 L 是 D 的取正向的边界曲线.
(一定要注意 L 的方向, 若方向相反, 则多一个负号. )
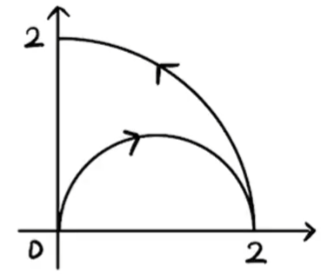 ,补线后
,补线后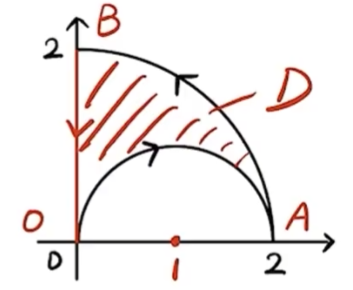
∬D(∂x∂Q−∂y∂P)dx dy=3x2+1−3x2=1
补线 L3 为 y 轴上从点 (0,2) 到点 (0,0) 的有向线段.
- 形成的封闭区域为D={(x,y)∣0⩽x⩽2,2x−x2⩽y⩽4−x2},
则由格林公式知
- ∫L+L33x2y dx+(x3+x−2y)dy∬D(∂x∂Q−∂y∂P)dx dy∬D(3x2+1−3x2)dx dy
- =∬D1 dx dy
- =41⋅π⋅22−21⋅π⋅12=2π
- ∫L33x2y dx+(x3+x−2y)dyx=00+∫L3(0+0−2y)dy=∫20(−2y)dy=4
I=∫L+L3−∫L3=2π−4.
(20)
(本题满分 11 分)
设 A=100aa1000a1000a1,β=1−100.
( I ) 计算行列式 ∣A∣;
(II) 当实数 a 为何值时, 方程组 Ax=β 有无穷多解, 并求其通解.
(20)
( I )解
- ∣A∣=100aa1000a1000a1=100a100a1−aa100a100a=1−a4.(II) 解法 1 因为方程组 Ax=β 有无穷多解的必要条件是其系数矩阵 A 的行列式为零, 即 ∣A∣=0, 由( I ) 得 1−a4=0, 从而 a=1 或 a=−1.
当 a=1 时,对方程组 Ax=β 的增广矩阵作初等行变换,有 - (A:β)=10011100011000111−100→1000110−1011000111−10−1→10001100011000101−10−2,由此知系数矩阵 A 的秩 r(A)=3, 增广矩阵的秩 r(A:β)=4, 二者不相等, 故当 a=1 时, 方程组 Ax=β 无解.
当 a=−1 时,(A;β)=100−1−11000−11000−111−100→1000−110−10−11000−111−101 - →1000−11000−11000−101−100,由此知 r(A)=r(A:β)=3<4, 故当 a=−1 时,方程组 Ax=β 有无穷多解. x3=x4, 故基础解系为 (1,1,1,1)T. 不难求得非齐次方程组的一个特解为 (0,−1,0,0)T, 从而得通解为
- x=0−100+k1111其中 k 为任意常数.
解法 2 直接对含参数 a 的增广矩阵 (A:β) 作初等行变换: - (A⋮β)=100aa1000a1000a11−100→1000a10−a20a1000a11−10−a
- →1000a1000a1a300a11−10−a−a2→1000a1000a1000a1−a41−10−a−a2.由于当且仅当 r(A)=r(A⋮β)<4 时, 方程组 Ax=β 有无穷多解, 故有 1−a4=0 且 −a−a2=0, 得 a=−1, 即 a=−1 时, 方程组 Ax=β 有无穷多解.
通解求解过程同解法 1.
(21)
(本题满分 11 分)
已知 A=10−10010a11a−1, 二次型 f(x1,x2,x3)=xT(ATA)x 的秩为 2 .
(I) 求实数 a 的值;
(II) 求正交变换 x=Qy 将二次型 f 化为标准形.
(21)
( I ) 解法 1 对 A 作初等行变换,得
- A=10−10010a11a−1→1000010011a+1−a−1→1000010011a+10因为 2=r(ATA)=r(A), 所以 a=−1.
解法 2ATA=201−a01+a21−a1−a1−a3+a2由已知 r(ATA)=2, 故 - ATA=201−a01+a21−a1−a1−a3+a2=(a+1)2(3+a2)=0,从而得 a=−1.
(II) 解 由( I) 知 a=−1, 得 - ATA=202022224故矩阵 ATA 的特征多项式为
- λE−ATA=λ−20−20λ−2−2−2−2λ−4=λ(λ−2)(λ−6),故 ATA 的特征值为 λ1=2,λ2=6,λ3=0.
当 λ1=2 时,解方程组 - ⎩⎨⎧−2x3=0,−2x3=0,−2x1−2x2−2x3=0,得相应的特征向量 1−10, 单位化后为 α1=211−10;
当 λ2=6 时,解方程组 - ⎩⎨⎧4x1−2x3=0,4x2−2x3=0,−2x1−2x2+2x3=0,得相应的特征向量 112, 单位化后为 α2=61112;
当 λ3=0 时,解方程组 - ⎩⎨⎧−2x1−2x3=0,−2x2−2x3=0,−2x1−2x2−4x3=0,得相应的特征向量 11−1, 单位化后为 α3=3111−1.
于是得到正交矩阵 - Q=21−2106161623131−31.在正交变换 x=Qy 下, 二次型的标准形为 f=2y12+6y22.
(22)
(本题满分 11 分)
设二维离散型随机变量 (X,Y) 的概率分布为
| X\Y | 0 | 1 | 2 |
|---|
| 0 | 41 | 0 | 41 |
| 1 | 0 | 31 | 0 |
| 2 | 121 | 0 | 121 |
| (I) 求 P{X=2Y}; | | | |
| (II) 求 Cov(X−Y,Y). | | | |
(22)
解
(I) 求 P{X=2Y}
- 找取值X=2Y,则
- 从概率分布表中,满足 X=2Y 的组合有:(X=0,Y=0) 和 (X=2,Y=1)
- 根据给定的概率分布,找出满足 X=2Y 的所有 (X,Y) 组合的概率之和
- P{X=2Y}=P{X=0,Y=0}+P{X=2,Y=1}=41
(II)
- 先写出X,Y,XY的分布函数(先取值,求概率)
- X∼(021131261)
- Y∼(031131231)
- XY∼(01271314121)
- 求 Cov(X−Y,Y)=Cov(X,Y)−Cov(Y,Y)Cov(X,Y)=E(XY)−E(X)E(Y)Cov(Y,Y)=D(Y)E(XY)−E(X)E(Y)−D(Y)D(Y)=E(Y2)−(EY)2
- 需要计算 E(X), E(Y), E(Y2), E(XY), 和 D(Y)
- 求协方差Cov(X,Y)
- E(X)=0⋅21+1⋅31+2⋅61=32
- EY=0⋅31+1⋅31+2⋅31=1
- E(XY)=0⋅127+1⋅31+4⋅121=32
- 求方差D(Y)
- E(Y2)=02⋅31+12⋅31+22⋅31=35
- D(Y)=E(Y2)−(EY)2E(Y2)=35EY=135−1=32
- 计算 Cov(X−Y,Y)
- Cov(X−Y,Y)=E(XY)−E(X)E(Y)−D(Y)==32−32×1−32=−32.
因此,P{X=2Y}=41 并且 Cov(X−Y,Y)=−32。
(23)
(本题满分 11 分)
设随机变量 X 与 Y 相互独立且分别服从正态分布 N(μ,σ2) 与 N(μ,2σ2), 其中 σ 是未知参数 且 σ>0. 记 Z=X−Y.
(I) 求 Z 的概率密度 f(z;σ2);
(II) 设 Z1,Z2,⋯,Zn 为来自总体 Z 的简单随机样本, 求 σ2 的最大似然估计量 σ2;
(III) 证明 σ2 为 σ2 的无偏估计量.
(23)
解
问题 I:求 Z 的概率密度 f(z;σ2)
- 已知条件
- X∼N(μ,σ2)
- Y∼N(μ,2σ2)
- Z=X−Y
- 有限个独立的正态分布的线性组合还是正态分布
- 计算 Z 的期望和方差
- 期望:EZ=E(x−y)=Ex−EY=0
- 方差:DZ=D(x−Y)=8x+DY=σ2+2σ2=3σ2
- 得出 Z 的分布
- Z∼(期望,方差)N(0,3σ2)
- 写出 Z 的概率密度函数
- 先要知道正态分布的密度函数:f(x)=2πσ1e−2σ2(x−μ)2(x∈R.)将Z∼N(0,3σ2)代入
- f(z,σ2)=2π3σ21⋅e−2⋅3σ2x2化简6πσ1e−6σ2x2
问题 II:求 σ2 的最大似然估计量 σ2
- 似然函数的构建和求解:把每个样本对应的概率密度相乘
- 构建基于 Zi 的似然函数
- L(σ2)=i=1∏nf(zi;σ2)=(6πσ1)ne−6σ21∑i=1nzi2
- 求解最大似然估计量
- 对似然函数取对数
- lnL(σ2)=−2nln(6πσ2)−6σ21i=1∑nzi2拆成加法−2nln6π−2nlnσ2−6σ21i=1∑nzi
- 并对σ2这个整体求导:dσ2dlnσ2=−2n⋅σ21+61i=1∑nzi2σ41=0
- 解方程移项,得σ41b1i=1∑nzi2=2nσ21
- 再次移项,得σ2=3n1i=1∑nzi2
问题 III:证明 σ2 是无偏估计量
- 证明无偏估计就是计算期望
- 计算 σ2 的期望
- E(σ2)=3n1E(i=1∑nzi2)将求和提出来3n1i=1∑nE(Zi2)
- 求和就是乘n3n1⋅nE(z2)求平方的期望转化为求期望和方差31(Dz+正态=0Ez2)
- 展开并简化
- E(σ2)=31DZ=σ2
- 得出结论
- σ2 是无偏的
- 因为 E(σ2)=σ2
这个二叉树结构清晰地展示了每一部分的求解步骤及其逻辑关系,帮助理解如何求出 Z 的概率密度函数、σ2 的最大似然估计量,并证明这个估计量是无偏的。
(I ) 因 X 与 Y 相互独立, 所以 Z=X−Y 服从正态分布, 且 EZ=0,DZ=DX+DY=3σ2, 故 Z 的概率密度为
- f(z;σ2)=6πσ21e−σ0z2,−∞<z<+∞.(II) 解 设 z1,z2,⋯,zn 为样本 Z1,Z2,⋯,Zn 的观测值, 则似然函数为
- L(σ2)=i=1∏nf(zi;σ2)=(6πσ2)−2nexp{−6σ21i=1∑nzi2},
- lnL(σ2)=−2nln(6πσ2)−6σ21i=1∑nzi2.令 dσ2d[lnL(σ2)]=−2σ2n+6σ41i=1∑nzi2=0, 解得 σ2=3n1i=1∑nzi2, 故 σ2 的最大似然估计量为
- σ^2=3n1i=1∑nZi2(III) 证 因 E(σ^2)=3n1i=1∑nE(Zi2)=31E(Z2)=31DZ=σ2, 所以 σ^2 是 σ2 的无偏估计量.

 ,积分区域投影后,
,积分区域投影后,
 ,补线后
,补线后