一、选择题
(本题共 8 小题,每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有 一项符合题目要求,把所选项前的字母填在题后的括号内. )
(1)
设函数 f(x) 在 (−∞,+∞) 上连续, 其 2 阶导函数 f′′(x) 的图形 如右图所示,
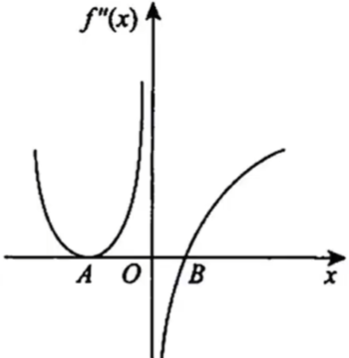
则曲线 y=f(x) 的拐点个数为 ()(A) 0 .
( B ) 1 .
(C) 2 .
( D) 3 .
(1)
- 答 应选 (C).
- f′′(x) 的零点有 2 个
- A 点两侧 f′′(x) 恒正, 所对应的点不是 y=f(x) 的拐点.
- B 点两侧 f′′(x) 异号, 所对应的点是 y=f(x) 的拐点.
- 虽然 f′′(0) 不存在, 但点 x=0 两侧 f′′(x) 异号, 因而 (0,f(0)) 是 y=f(x) 的拐点.
- 因此共有 2 个拐点.
(2)
设 y=21e2x+(x−31)ex 是二阶常系数非齐次线性微分方程 y′′+ay′+by=cex 的一个特解, 则 ( )
(A) a=−3,b=2,c=−1.
(B) a=3,b=2,c=−1.
(C) a=−3,b=2,c=1.
(D) a=3,b=2,c=1.
(2)
- 答 应选(A).
- 本题主要考查微分方程的解的概念.
- 已知微分方程的一个特解,要求原方程的系数。
- 可以直接将解代入原方程,然后比较等式两端的系数求出未知参数。
- y=21e2x+(x−31)ex
- y′=21⋅2⋅e2x+ex+(x−31)⋅ex=e2x+(x+32)ex
- y′′=2e2x+ex+(x+32)ex=2e2x+(x+35)ex
- 将上面求的y,y′,y′′代入 y′′+ay′+by=cex 中
- 2e2x+(x+35)ex+ae2x+a(x+32)ex+2be2x+b(x−31)ex=cex
- 整理得,(2+a+21b)e2x+(1+a+b)xex+(35+32a−31b)ex=cex
- 比较上式两端系数, 得到 ⎩⎨⎧2+a+21b=0,1+a+b=0,35+32a−31b=c,
- 解得 ⎩⎨⎧a=−3,b=2,c=−1, 故选 A.
方法2
- 由特解 y=21e2x−31ex+xex 知,
- 方程的特征根为 r1=2,r2=1,
- 特征方程为 (r−2)(r−1)=0, 即 r2−3r+2=0.
- 又原方程的特征方程为 r2+ar+b=0, 于是 a=−3,b=2.
- 将特解 y∗=xex,求y′和y′′代入原方程得
- (xex)′′−3(xex)′+2xex=(x+2)ex−3(x+1)ex+2xex=−ex=cex,
- 因此 c=−1
(3)
若级数 n=1∑∞an 条件收敛, 则 x=3 与 x=3 依次为幂级数 n=1∑∞nan(x−1)n 的 ()(A) 收敛点,收敛点.
(B) 收玫点, 发散点.
(C) 发散点,收敛点.
(D) 发散点, 发散点.
(3)
- 答 应选(B).
解 由 n=1∑∞an 条件收敛可知 n=1∑∞antn 的收敛半径 R=1 (若 R<1, 则 n=1∑∞antnt=1=n=1∑∞an 发散; 若 R>1, 则 n=1∑∞antnt=1=n=1∑∞an 绝对收玫,均矛盾), 故 n=1∑∞nantn=tn=1∑∞nantn−1=tn=1∑∞(antn)′ 的收敛半径 R=1 (逐项求导不改变收敛半径). 则
当 x=3 时, n=1∑∞nan(3−1)n 绝对收玫 (0<3−1<1);
当 x=3 时, n=1∑∞nan(3−1)n=n=1∑∞nan2n 发散 (2>1).
注 本题用到一个基本结论: 若幂级数 n=1∑∞anxn 在 x=x0 处条件收敛,则 x=x0 是该基级数收敛区间 的一个端点.
(4)
设 D 是第一象限中的曲线 2xy=1,4xy=1 与直线 y=x,y=3x 围成的平面区域, 函数 f(x,y) 在 D 上连续, 则 ∬Df(x,y)dx dy=()
(A) ∫4π3π dθ∫2sin2θ1sin2θ1f(rcosθ,rsinθ)r dr.
(B) ∫4π3π dθ∫2sin2θ1sin2θ1f(rcosθ,rsinθ)r dr.
(C) ∫4π3π dθ∫2sin2θ1sin2θ1f(rcosθ,rsinθ)dr.
(D) ∫4π3π dθ∫2sin2θ1sin2θ1f(rcosθ,rsinθ)dr.
(4)
- 答 应选(B).
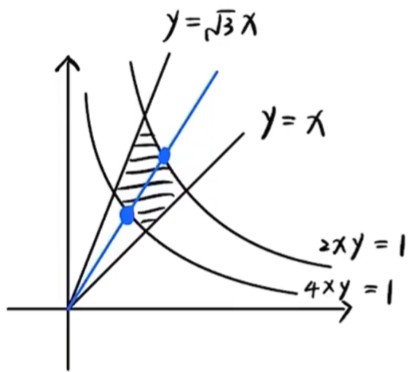
- 区域 D 如图所示. 作极坐标变换, 将 ∬Df(x,y)dx dy 化为二次积分.
- 2xy=1⇒2r2sinθcosθ=1
- r2sin2θ=1
- r=sin2θ1
- 4xy=1⇒4r2sinθcosθ=1
- r2⋅2sin2θ=1
- r=2sin2θ1
- D 的极坐标范围是
- 4π⩽θ⩽3π
- 2sin2θ1⩽r⩽sin2θ1
- 因此∬Df(x,y)dx dy=∫4π3π dθ∫2sin2θ1sin2θ1f(rcosθ,rsinθ)r dr
(5)
设矩阵 A=1111241aa2,b=1dd2. 若集合 Ω={1,2}, 则线性方程组 Ax=b 有无 穷多解的充分必要条件为 ( )
( A ) a∈/Ω,d∈/Ω.
( В) a∈/Ω,d∈Ω.
( C) a∈Ω,d∈/Ω.
(D) a∈Ω,d∈Ω.
(5)
- 答 应选(D).
解 Ax=b 有无穷多解 ⇔r(A;b)=r(A)<3.∣A∣ 是一个范德蒙德行列式, 值为 (a−1)(a−2).
若 a∈/Ω, 则 ∣A∣=0,r(A)=3, 此时 Ax=b 有唯一解, (A), (B) 排除;
类似地,若 d∈/Ω, 则 r(A:b)=3, (C) 排除;
当 a∈Ω,d∈Ω 时, r(A;b)=r(A)=2,Ax=b 有无穷多解. 选(D).
(6)
设二次型 f(x1,x2,x3) 在正交变换 x=Py 下的标准形为 2y12+y22−y32, 其中 P=(e1,e2,e3). 若 Q=(e1,−e3,e2), 则 f(x1,x2,x3) 在正交变换 x=Qy 下的标准形为 ()(A) 2y12−y22+y32.
(B) 2y12+y22−y32.
( C) 2y12−y22−y32.
(D) 2y12+y22+y32.
(6)
- 答 应选(A).
解 设二次型矩阵为 A, 则 - P−1AP=PTAP=20001000−1, e1,e2,e3 分别是 A 的对应于特征值 2,1,-1 的特征向量. 于是一 e3 也是 A 的对应于特征值一 1 的特征向 因此Q−1AQ=QTAQ=2000−10001, 而 f 在正交变换 x=Qy 下的标准形为 2y12−y22+y32.
(7)
若 A,B 为任意两个随机事件, 则 ( )(A) P(AB)⩽P(A)P(B).(B) P(AB)⩾P(A)P(B).(C) P(AB)⩽2P(A)+P(B).(D) P(AB)⩾2P(A)+P(B).
(7)
解
- 分析选项
- 考察 P(AB) 与 P(A)、P(B) 的关系
- 选项 (A) 和 (B) 涉及 P(AB) 与 P(A)P(B) 的比较
- 选项 (C) 和 (D) 涉及 P(AB) 与 2P(A)+P(B) 的比较
- 确定正确选项
- 由 P(AB)⩽P(A) 和P(AB)⩽P(B)
- 两者相加得,得 2P(AB)⩽P(A)+P(B)移项P(AB)⩽2P(A)+P(B)
- 正确选项是 (C)
(8)
设随机变量 X,Y 不相关, 且 E(X)=2,E(Y)=1,D(X)=3, 则 E[X(X+Y−2)]=()(A) -3 .(B) 3 .(C) -5 .(D) 5 .
(8)
- 已知条件
- X 和 Y 不相关,意味着 E(XY)=E(X)E(Y)。
- E(X)=2,E(Y)=1,D(X)=3。
- 计算 E[X(X+Y−2)]
- 展开表达式得到 E[X(X+Y−2)]=E(X2)+E(XY)−2E(X)。
- 使用 E(X2)=D(X)+(E(X))2:
- E(X2)=D(X)+(E(X))2=3+22=7。
- 使用 X 和 Y 不相关的性质计算 E(XY):
- E(XY)=E(X)E(Y)=2×1=2。
- 现在将值代入表达式:
- E[X(X+Y−2)]=7+2−2×2=5。
因此,E[X(X+Y−2)]=5,答案是选项 (D)。
(9)
x→0limx2ln(cosx)=
(9)
答 应填 −21.
- 等价无穷小代换(本质是泰勒)
- 利用等价无穷小代换,ln(1+x)∼x 当 u→0。
- 所以 ln(cosx)=ln(1+cosx−1)∼cosx−1。
- 又因为 cosx−1∼−21x2 当 x→0(使用等价无穷小)
- 因此,x→0limx2ln(cosx)=x→0limx2−21x2=−21。
(10)
∫−2π2π(1+cosxsinx+∣x∣)dx=
(10)
- 计算积分 ∫−2π2π(1+cosxsinx+∣x∣)dx。
- 将积分分为两部分。
- 第一部分:∫−2π2π1+cosxsinx dx。
- 区间对称,考虑被积函数是奇函数还是偶函数
- 由于 1+cosxsinx 是奇函数,其在对称区间的积分为0。
- 第二部分:偶函数翻倍=2∫02πx dx。
- 计算 ∣x∣ 在 [−2π,2π] 区间的积分。
- 因 ∣x∣ 在 [0,2π] 为 x,且函数是偶函数,故积分范围变为 [0,2π] 的两倍。
- 计算 ∫02πx dx。
- 使用基本积分公式。
- 得到 x202π=4π2。
- 合并两部分结果。
- 第一部分结果为0,第二部分结果为 4π2。
- 最终结果为 4π2
(11)
若函数 z=z(x,y) 由方程 ez+xyz+x+cosx=2 确定, 则 dz∣(0,1)=
(11)
解
本解法不是最优解法
该问题涉及求函数 z=z(x,y),由方程 ez+xyz+x+cosx=2 确定,在点 (0,1) 的微分 dz。
- 因为隐函数方程中有z,所以求出 z(0,1)的具体值
- 代入 x=0 和 y=1 到原方程,得 ez(0,1)+0+0+cos0=2。
- 解方程得 z(0,1)=0。
- 求偏导数 ∂x∂z 和 ∂y∂z。
- 对原方程关于 x 求偏导数得:ez∂x∂z+yz+xyz∂x∂z+1−sinx=0。
- 对原方程关于 y 求偏导数得:ez∂y∂z+xz+xyz∂y∂z=0。
- 先代值,再移项,求点 (0,1) 偏导数的值
- 代入 x=0,y=1,z=0 得:
- ∂x∂z(0,1)=−1
- ∂y∂z(0,1)=0
- 写出全微分公式
- 使用全微分公式得:dz∣(0,1)=∂x∂z(0,1)dx+∂y∂z(0,1)dy=−dx
(12)
设 Ω 是由平面 x+y+z=1 与三个坐标平面所围成的空间区域, 则 ∭Ω(x+2y+3z)dx dy dz =
(12)
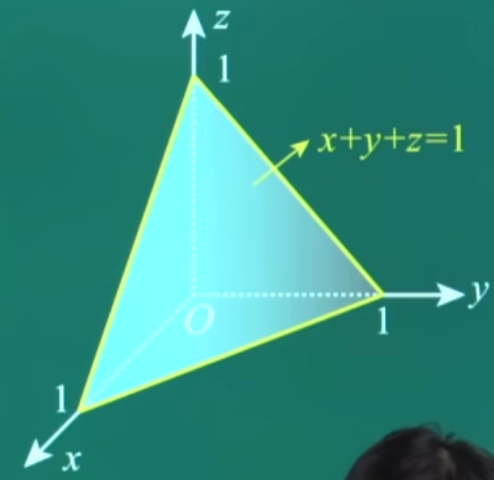 ,
,- (2) 轮换对称性
若将表示积分区域 Ω 的表达式中的 x,y,z 轮换后表达式不变, 则将被积函数中 x,y,z 作相应的轮换后积分值不变,即 - ∭Ωf(x,y,z)dx dy dz=∭Ωf(y,z,x)dx dy dz=∭Ωf(z,x,y)dx dy dz
- =31∬Ω[f(x,y,z)+f(y,z,x)+f(z,x,y)]dx dy dz.
- 由轮换对称性知,∭Ωx dx dy dz=∭Ωy dx dy dz=∭Ωz dx dy dz.
- 又 Ω={(x,y,z)∣(x,y)∈Dx,0⩽z⩽1},
- 其中 Dx={(x,y)∣x+y⩽1−z,y⩾0,z⩾0},
- 其面积为 2(1−z)2,
投影
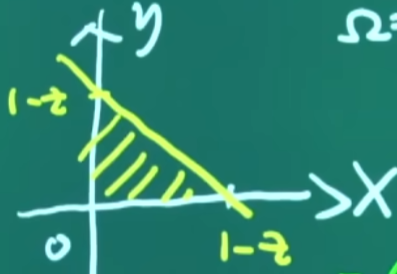
- ∭Ω(x+2y+3z)dx dy dz=6∭Ωz dx dy dz
- 其中∭Ωz dx dy dz
- =∫01z dz∬Dx dx dy
- =∫01z⋅2(1−z)2 dx
- =21∫01(z3−2z2+z)dz
- =21(4z2−32−32+2z2)01=241
(13)
n 阶行列式 2−1⋮0002⋮00⋯⋯⋯⋯00⋮2−122⋮22=
(13)
- [9.29](file:///C:/Users/wangpanfeng/Videos/01.%E6%95%B0%E5%AD%A6%E4%B8%80/02.2015%E5%B9%B4%E6%95%B0%E4%B8%80%E7%9C%9F%E9%A2%98/02.2015%E5%B9%B4%E8%80%83%E7%A0%94%E6%95%B0%E5%AD%A6%E7%9C%9F%E9%A2%98%E5%A1%AB%E7%A9%BA%E9%A2%98%EF%BC%88%E6%95%B0%E4%B8%80%EF%BC%89.mp4#t=09:29)
- 答 应填 2n+1−2.解法 1 递推法. 将此行列式记为 Dn, 按第 n 行展开, 得 Dn=(−1)2n−1⋅(−1)Dn−1+2n=Dn−1+2n, 得到递推公式 Dn=Dn−1+2n(n>1). 于是Dn=Dn−1+2n=Dn−2+2n−1+2n=⋯=D1+22+23+⋯+2n
- =2+22+23+⋯+2n=2n+1−2.解法 2 作初等行变换, 把第 1 行消到只剩最右边一个非零元索.做法如下:第 1 行加第 2 行的 2 倍, 加第 3 行的 22 倍, ⋯, 加第 n 行的 2n−1 倍, 使得第 1 行成为 0,0 , 0,⋯,0,a, 其中 a=2+4+8+⋯+2n=2n+1−2. 再按第 1 行展开, 得 Dn=2n+1−2.注 本题还有多种解法,如按第 1 行展开得递推公式 Dn=2Dn−1+2; 作初等行变换,化原行列式为上 三角行列式(做法为自上而下, 把各行的 21 倍加到下一行, 于是消去了对角线下所有的 -1 ); 作初等行变 换,消去第 1 行到第 n−1 行上的对角线元素 2 (做法为自下而上,把各行的 2 倍加到上一行) 等.
(14)
设二维随机变量 (X,Y) 服从正态分布 N(1,0;1,1;0),则 P{XY−Y<0}=
(14)
- 解
- 二维随机变量 (X,Y) 的分布
- (X,Y) 服从二维正态分布 N(1,0;1,1;0),意味着
- X∼N(1,1)(X 服从均值为 1,方差为 1 的正态分布)
- Y∼N(0,1)(Y 服从均值为 0,方差为 1 的正态分布)
- X 和 Y 相互独立
- 转换 X
- X−1 也服从标准正态分布 N(0,1)
- 因为 X 的均值为 1,减去均值后得到 X−1∼N(0,1)
- 计算 P{XY−Y<0}分配律P{(X−1)Y<0}
- 因为X-1和Y相互独立,所以:
- P{(X−1)Y<0}一正一负不能同正同负P{X−1<0,Y>0}+P{X−1>0,Y<0}
- X−1和Y相互独立P{X−1<0}⋅P{Y>0}+P{X−1>0}⋅P{Y<0}
- 由于 X−1 和 Y 都服从标准正态分布,它们小于或大于 0 的概率都是 1/2(对称轴两边一半一半)
- =2×Φ(0)×[1−Φ(0)]
- =2×21×21=21
所以,P{XY−Y<0}=21。
(15)
(本题满分 10 分)设函数 f(x)=x+aln(1+x)+bxsinx,g(x)=kx3. 若 f(x) 与 g(x) 在 x→0 时 是等价无穷小, 求 a,b,k 值.
(15)
- 泰勒展开 ln(1+x) 和 sinx:
- ln(1+x)=x−2x2+3x3+o(x3)
- sinx=x−6x3+o(x3)
- 将展开式的ln和sin代入回 f(x):
- f(x)=x+a(x−2x2+3x3)+bx(x−6x3)+o(x3)
- 合并同阶得到:
f(x)=(1+a)x+(b−2a)x2+(3a−6b)x3+o(x3)
- 由于 f(x) 和 g(x)=kx3 在 x→0 时等价,
比较 f(x) 和 g(x)同次幂的系数 - 我们需要 f(x) 的一次和二次项消失且三次项系数字等于 k,
1+a=0,b−2a=0,3a−6b=k
- 求解 a, b, 和 k:
- 从 1+a=0 得到 a=−1。
- 将a代入,从 b−2a=0 得到 b=−21。
- 将a和b代入,从 3a−6b=k 得到 k=−31。
(16)
(本题满分 10 分)设函数 f(x) 在定义域 I 上的导数大于零. 若对任意的 x0∈I, 曲线 y=f(x) 在点 (x0,f(x0)) 处 的切线与直线 x=x0 及 x 轴所围成区域的面积恒为 4 , 且 f(0)=2, 求 f(x) 的表达式.
(16)
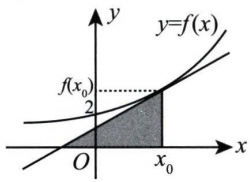
- ① 写出切线方程:y−f(x0)=f′(x0)(X−x0)
- ② 计算区域面积.
- 一条直角边长: ∣f(x0)∣.
- 另一条直角边长: ∣x∗−x0∣.
- 在(1)式中, 令 y=0, 可得:−f(x0)=f′(x0)(x∗−x0)
- ∣x∗−x0∣=f′(x0)f(x0)
- S=21底×高=21∣f(x0)∣⋅f′(x0f(x0)=21f′(x0)[f(x0)]2=4
- y=f(x0)8y′=y2.
- 分离变量, 得 y28 dy=dx.
- 方程两端积分, 得 −y8=x+C, 其中 C 为待定常数.
- 由于 f(0)=2,故 C=−4,
- 从而 y=4−x8
(17)
(本题满分 10 分)已知函数 f(x,y)=x+y+xy, 曲线 C:x2+y2+xy=3, 求 f(x,y) 在曲线 C 上的最大方向导数.
(17)
- 解题过程
- 目标函数:梯度的模长
- 约束条件:x2+y2+xy=3。
- 求梯度的模长
- 函数:f(x,y)=x+y+xy
- 函数的梯度:⇒(fx,fy)=(1+y,1+x)
- 然后是梯度的模长等于坐标平方和
- 构造拉格朗日函数
- 目标函数:g(x,y)=(1+x)2+(1+y)2。
- 由于求模的最大值与求模的平方的最大值等价,
- 故为了方便计算, 我们没有令 g(x,y)=fx′2+fy′2, 而是令 g(x,y)=fx′2+fy′2.
- 约束条件:φ(x,y)=x2+y2+xy−3=0。
- 作拉格朗日函数:L(x,y,λ)=g(x,y)+λφ(x,y)=(1+y)2+(1+x)2+λ(x2+y2+xy−3)
- ⎩⎨⎧①Lx′=2(1+x)+λ(2x+y)=0,②Ly′=2(1+y)+λ(2y+x)=0,③Lλ′=x2+y2+xy−3=0.
- (1)−(2), 得
- 2(x−y)+λ(x−y)=0
- (λ+2)(x−y)=0
- 分情况讨论
- (1) x=y :
- 3x2=3
- ⇒{x=1y=1 或 {x=−1y=−1.
- (2) λ=−2 : 代入(1)
- 2(1+x)−2(2x+y)=0
- x+y−1=0,代入消元法,代入(3)
- x2+(1−x)2+x(1−x)=3
- x2−x−2=0
- 得x=−1,x=2
- 则g(x,y)=(1+x)2+(1+y)2有四个可能的极值点(1,1)(−1,−1),(2,−1),(−1,2)
- g(1,1)=8
- g(−1,−1)=0
- g(2,−1)=g(−1,2)=9
- 故 g(x,y) 在条件 x2+y2+xy=3 下的最大值为 9 ,
从而 f(x,y) 在曲线 C 上的最大方向导数为 3 . - 若函数 f(x,y,z) 在点 (x0,y0,z0) 处可微分, el=(cosα,cosβ,cosγ) 是与方向 l 同向的单位向量, 则∂l∂f(x0,y0,z0)=gradf(x0,y0,z0)⋅el=∣gradf(x0,y0,z0)∣cosθ
- 这里 θ 为向量 gradf(x0,y0,z0) 与向量 el 的夹角.
- 当 θ=0 时, 即 el 与梯度 gradf(x0,y0,z0) 方向相同时, 函数 f(x,y,z) 沿这个方向增加最快, 且在这个方向的方向导数达到最大, 此时 ∂l∂f(x0,y0,z0)=∣gradf(x0,y0,z0)∣.
- 当 θ=π 时,即 et 与梯度 gradf(x0,y0,z0) 方向相反时, 函数 f(x,y,z) 沿这个方向减少最快, 且在这个方向的方向导数达到最小, 此时 ∂l∂f(x0,y0,z0)=−∣gradf(x0,y0,z0)∣.
- 当 θ=2π 时,即 el 与梯度 gradf(x0,y0,z0) 正交时,函数 f(x,y,z) 沿这个方向的变化率为 0 , 此时 ∂l∂f(x0,y0,z0)=0.
(18)
(本题满分 10 分)(抽象题)
(I ) 设函数 u(x),v(x) 可导,利用导数定义证明 [u(x)v(x)]′=u′(x)v(x)+u(x)v′(x);(II) 设函数 u1(x),u2(x),⋯,un(x) 可导, f(x)=u1(x)u2(x)⋯un(x), 写出 f(x) 的求导公式.
(18)
- (I ) 证 因为函数 u(x),v(x) 可导,所以Δx→0limΔxu(x+Δx)−u(x)=u′(x),Δr→0limΔxv(x+Δx)−v(x)=v′(x), 且 Δx→0limv(x+Δx)=v(x).从而[u(x)v(x)]′=Δ→0limΔxu(x+Δx)v(x+Δx)−u(x)v(x)
- =Δx→0limΔxu(x+Δx)v(x+Δx)−u(x)v(x+Δx)+u(x)v(x+Δx)−u(x)v(x)
- =Δx→0lim[Δxu(x+Δx)−u(x)v(x+Δx)+u(x)Δxv(x+Δx)−v(x)]
- =Δx→0limΔxu(x+Δx)−u(x)⋅Δx→0limv(x+Δx)+u(x)Δx→0limΔxv(x+Δx)−v(x)
- =u′(x)v(x)+u(x)v′(x).(II ) 解 f′(x)=u1′(x)u2(x)⋯un(x)+u1(x)u2′(x)⋯un(x)+⋯+u1(x)u2(x)⋯un′(x).注 这是继 2008,2009 年后又一次考查基本定理(性质)、基本公式的推导, 本题和 2008 年的 (18)题 都是在考査导数的定义, 这是高等数学中一个非常重要的定义, 但可惜, 不论是 2008 年的变限积分求导公 式还是 2015 年的乘积求导公式(本题), 考生作答得都不够理想,究其原因还是基础不够扎实.
(19)
(本题满分 10 分)已知曲线 L 的方程为 {z=2−x2−y2z=x, 起点为 A(0,2,0), 终点为 B(0,−2,0), 计算曲线积 分 I=∫L(y+z)dx+(z2−x2+y)dy+x2y2 dz.
(19)
斯托克斯(一阶连续偏导)
- (2)看题目要求是否说明有一阶连续偏导,否则用投代积
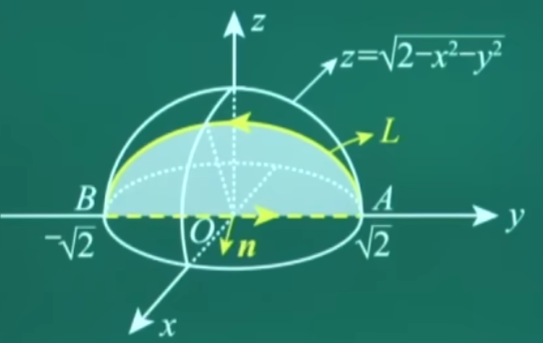
- 斯托克斯公式直接化为第一类曲面积分
空间平面怎么算
空间曲面怎么算
∮ΓP dx+Q dy+R dz=∬Σcosα∂x∂Pcosβ∂y∂Qcosγ∂z∂RdS- 其中 n=(cosα,cosβ,cosγ) 为有向曲面 Σ 在点 (x,y,z)处的单位法向量.
- 解题思路
- ∮L+L′斯托克斯∫Σ∣∣ds.
- ∮L+L′−∮L′=I
- 设 L1 是从点 B 到点 A 的直线段, Σ 为平面 z=x 上由 L 与 L1 围成的半圆面下侧,其面积为 π,单位法向量为 (21,0,−21)
- z:z=x,则x−z=0
- 法向量:(1,0,−1)
- 单位向量:(cosα,cosβ,cosγ)=(21⋅0,−21)
- ∮L+L1(y+z)dx+(z2−x2+y)dy+x2y2 dz. 由斯托克斯公式知,
- =∬Σ21∂x∂y+z0∂y∂z2−x2+y−21∂z∂x2y2dS
- 按第一行展开∬Σ[21(2x2y−2z)+(−21)(−2x−1)]dS
- 提出2121∬z(2x2y−2z+2x+1)dS
- z=x21∬Σ(2x2y+1)dS
- 由于曲面 Σ 关于 xOz 平面对称, 且函数 2x2y 是关于 y 的奇函数, 故 ∬Σ2x2y dS=0,
- =21∬ΣdS=21⋅Σ 的面积
- S=21⋅π⋅(2)2半圆的面积22π
- 因此, I=22π−0=22π.
参数方程(连续函数)
- a. 一投二代三计算.(参数方程分为直角坐标和极坐标)
- 设 Γ:⎩⎨⎧x=x(t),y=y(t),t:a→b,z=z(t),, 则有
- ∫ΓP dx+Q dy+R dz
- =∫ab{P[x(t),y(t),z(t)]x′(t)+Q[x(t),y(t),z(t)]y′(t)+R[x(t),y(t),z(t)]z′(t)}dt.
- dx=x′(t)dt
- dy=y′(t)dt
- dz=z′(t)dt
- 如何写出参数方程:已知 L:{z=2−x2−y2z=x
- z=xx=2−x2−y2两边平方x2=2−x2−y2
- 移项2x2+y2=2化为椭圆方程x2+2y2=1
- cos2t+sin2t=1⎩⎨⎧x=costy=2sintz=cost
- t∈[−2π,2π], 且 L 的起点 A 对应 t=2π, 终点对应参数 t=−2π
- I=∫L(y+z)dx+(z2−x2+y)dy+x2y2 dz.
- =∫2π−2π[(2sint+cost)(−sint)+cos2t−cos2t(2sint)⋅2cost+cos2t⋅2sin2t\cdotp(−sint)]dt
- 整理∫2π−2π(−2sin2t−sintcost+2sintcost−2sin3tcos2t)dt
- 整理∫2π2π(−2sin2t+sintcost−2sin3tcos2t)dt
- 区间对称奇函数为0−2∫2π−2πsin2tdt偶函数翻倍22∫02πsin2tdt
- 华里士22×21×2π=22π
- 二倍角公式也能算过程自己算
(20)
(本题满分 11 分)
设向量组 α1,α2,α3 为 R3 的一个基, β1=2α1+2kα3,β2=2α2,β3=α1+(k+1)α3.
( I ) 证明向量组 β1,β2,β3 为 R3 的一个基;
( II ) 当 k 为何值时,存在非零向量 ξ 在基 α1,α2,α3 与基 β1,β2,β3 下的坐标相同,并求所有的 ξ.
(20)
- (I ) 证 由于 (β1,β2,β3)=(2α1+2kα3,2α2,α1+(k+1)α3)=(α1,α2,α3)P, 其中
- P=202k02010k+1,且 ∣P∣=4=0, 所以 β1,β2,β3 为 R3 的一个基.
(II ) 解 设 ξ 在基 α1,α2,α3 与基 β1,β2,β3 下的坐标向里为 x, 则 - ξ=(α1,α2,α3)x=(β1,β2,β3)x=(α1,α2,α3)Px,所以
- $(P-E) x=0 .
- $对 P−E 作初等行变换
- P−E=102k01010k→10001010−k,所以当 k=0 时, 方程组 (P−E)x=0 有非零解, 且所有非零解为
- x=c10−1, 其中 c 为任意非零常数.
故在两个基下坐标相同的所有非零向量为 ξ=(α1,α2,α3)c0−c=c(α1−α3),c 为任意非零常数.
(21)
(本题满分 11 分)
设矩阵 A=0−1123−2−3−3a 相似于矩阵 B=100−2b3001.
(I) 求 a,b 的值;
(II) 求可逆矩阵 P,使 P−1AP 为对角矩阵.
(21)
- 解 (I ) 由于矩阵 A 与矩阵 B 相似,因此 tr(A)=tr(B),∣A∣=∣B∣, 于是
- 3+a=2+b,2a−3=b,解得
(II) 由 ( I ) 知 A=0−1123−2−3−34,B=100−253001.
由于矩阵 A 与矩阵 B 相似, 因此 ∣λE−A∣=∣λE−B∣=(λ−1)2(λ−5), 故 A 的特征值为 λ1=λ2=1,λ3=5.
当 λ1=λ2=1 时, 解方程组 (E−A)x=0, 得线性无关的特征向量 ξ1=210,ξ2=−301;
当 λ3=5 时,解方程组 (5E−A)x=0, 得特征向量 ξ3=−1−11.
令 P=(ξ1,ξ2,ξ3)=210−301−1−11, 则 P−1AP=100010005, 故 P 为所求可逆矩阵.
(22)
(本题满分 11 分)
设随机变量 X 的概率密度为
- f(x)={2−xln2,0,x>0,x⩽0.
对 X 进行独立重复的观测, 直到第 2 个大于 3 的观测值出现时停止, 记 Y 为观测次数.
( I ) 求 Y 的概率分布;
(II) 求 E(Y).
(22)
(I)
- 求 Y 的概率分布:Y是离散型的
- 找取值,求概率
- 找取值:直到第 2 个大于 3 的观测值出现时停止, 记 Y 为观测次数
- Y可能为2,3,4,5,一直到n,确定B~(n,p)
- 求p:一个观测值X大于 3 的概率 p,和Y没有关系
- p=P{X>3}=∫3+∞f(x)dx=∫3+∞2−xln2dx=−2−x3+∞=81
- 求p逆:
- P{X≤3}=1−81=87.
- Y 的概率分布(几何分布,不用考虑组合情况)
- Y 是直到第二个观测值大于 3 为止的观测次数
- P{Y=k} 是第 k 次观测时第二次得到大于 3 的值
- P{Y=k}=Ck−11⋅81⋅(87)k−2⋅81Ck−11=1!(k−1)641(k−1)(87)k−2,其中 k=2,3,⋯
(II) 求 E(Y)(Y 的期望值)
- 解法 2:使用几何分布(7×2表格)
- Y=Y1+Y2, 且 Y1,Y2 均服从参数为 p=81 的几何分布.
- E(Y)=E(Y1+Y2)=E(Y1)+E(Y2)=811+811=16
- 解法 1:直接计算(不推荐)
- E(Y)=k=2∑∞k(k−1)(87)k−2(81)2
- 使用级数求导和求和技巧
- E(Y)=(81)2(1−x)32x=87=16
(23)
(本题满分 11 分)
设总体 X 的概率密度为
- f(x;θ)={1−θ1,0,θ⩽x⩽1, 其他,
其中 θ 为未知参数. X1,X2,⋯,Xn 为来自该总体的简单随机样本.
(I) 求 θ 的矩估计量;
(II) 求 θ 的最大似然估计量.
(23)
- ( I ) 由于总体 X 服从区间 [θ,1] 上的均匀分布, 因此 EX=21+θ.
- 由 21+θ=Xˉ, 其中 Xˉ 为样本均值, 得 θ 的矩估计是 θ^=2Xˉ−1.
- 设 x1,x2,⋯,xn 为样本 X1,X2,⋯,Xn 的观测值,
- 写出似然函数为L(θ)=i=1∏nf(xi;θ)={(1−θ)n1,0,θ≤xi≤1(i=1,2,⋯,n)
- 为了方便求导,取对数:当θ⩽xi⩽1时,lnL(θ)=−nln(1−θ)
- 求导求驻点:dθdln((θ)=1−θn=0,因为分母不为0,所以分子为0,则n=0,出现错误
- 要使得dθdln((θ)=1−θn>0,θ越大,分母1−θ越小越趋向于0,则lnL(θ)越大
- θ的最大值为x的最小值θ≤min{x1,x2,⋯,xn}
- 故 θ 的最大似然估计量为θ^=min{X1,X2,⋯,Xn}


 ,
,

