一、选择题: 1 10 小题, 每小题 5 分, 共 50 分. 下列每题给出的四个选项中, 只有一个选项是最符合题目要求的 (1) 曲线 y = x ln ( e + 1 x − 1 ) y=x \ln \left(\mathrm{e}+\frac{1}{x-1}\right) y = x ln ( e + x − 1 1 ) y = x + e y=x+\mathrm{e} y = x + e y = x + 1 e y=x+\frac{1}{\mathrm{e}} y = x + e 1 y = x y=x y = x y = x − 1 e y=x-\frac{1}{\mathrm{e}} y = x − e 1 2025版 求斜渐近线的方法:y = k x + b \displaystyle y = kx + b y = k x + b lim x → ∞ ( y x ) = k \displaystyle \lim_{x \to \infty} \left(\frac{y}{x}\right) = k x → ∞ lim ( x y ) = k lim x → ∞ ( y − k x ) = b \displaystyle \lim_{x \to \infty} (y - kx) = b x → ∞ lim ( y − k x ) = b k = lim x → ∞ y x = 代入 y lim x → ∞ x ln ( e + 1 x − 1 ) x \displaystyle k = \lim_{x \to \infty} \frac{y}{x} \xlongequal[]{\text{代入}y} \lim_{x \to \infty} \frac{x \ln\left(e + \frac{1}{x-1}\right)}{x} k = x → ∞ lim x y 代入 y x → ∞ lim x x ln ( e + x − 1 1 ) = 消去 x lim x → ∞ ln ( e + 1 x − 1 ) → 1 x − 1 → 0 lim x → ∞ ln e = 1 \displaystyle \xlongequal[]{\text{消去}x}\lim_{x \to \infty} \ln\left(e + \frac{1}{x-1}\right) \xrightarrow{\frac{1}{x-1} \to 0} \lim_{x \to \infty} \ln e = 1 消去 x x → ∞ lim ln ( e + x − 1 1 ) x − 1 1 → 0 x → ∞ lim ln e = 1 b = lim x → ∞ ( y − k x ) = 代入 y 和 k lim x → ∞ x ln ( e + 1 x − 1 ) − x \displaystyle b \xlongequal[]{} \lim_{x \to \infty} (y - kx) \xlongequal[]{\text{代入}y\text{和}k}\lim_{x \to \infty} x \ln\left(e + \frac{1}{x-1}\right) - x b x → ∞ lim ( y − k x ) 代入 y 和 k x → ∞ lim x ln ( e + x − 1 1 ) − x = 提取系数 x lim x → ∞ x [ ln ( e + 1 x − 1 ) − 1 ] → 1 = ln e lim x → ∞ x ⋅ [ ln e + 1 x − 1 e ] \displaystyle \xlongequal[]{\text{提取系数}x}\lim_{x \to \infty} x \left[\ln\left(e + \frac{1}{x-1}\right) - 1\right] \xrightarrow{1 = \ln e} \lim_{x \to \infty} x \cdot \left[\ln\frac{e + \frac{1}{x-1}}{e}\right] 提取系数 x x → ∞ lim x [ ln ( e + x − 1 1 ) − 1 ] 1 = l n e x → ∞ lim x ⋅ [ ln e e + x − 1 1 ] = l n 里面做除法 lim x → ∞ x ⋅ ln [ 1 + 1 e ( x − 1 ) ] \displaystyle \xlongequal[]{ln\text{里面做除法}} \lim_{x \to \infty} x \cdot \ln\left[1 + \frac{1}{e(x-1)}\right] l n 里面做除法 x → ∞ lim x ⋅ ln [ 1 + e ( x − 1 ) 1 ] → ln ( 1 + x ) ∼ x lim x → ∞ x ⋅ 1 e ( x − 1 ) = 1 e \displaystyle \xrightarrow{\ln(1+x) \sim x} \lim_{x \to \infty} x \cdot \frac{1}{e(x-1)} = \frac{1}{e} l n ( 1 + x ) ∼ x x → ∞ lim x ⋅ e ( x − 1 ) 1 = e 1 结合斜率 k k k b b b y = k x + b = x + 1 e y = kx + b= x + \frac{1}{e} y = k x + b = x + e 1 gpt版 我们首先需要确定斜渐近线方程的两个关键元素:斜率 k k k b b b y = x ln ( e + 1 x − 1 ) y = x \ln \left(e + \frac{1}{x-1}\right) y = x ln ( e + x − 1 1 )
确定斜率 k k k k = lim x → ∞ y x = = lim x → ∞ x ln ( e + 1 x − 1 ) x = lim x → ∞ ln ( e + 1 x − 1 ) = ln e = 1 \displaystyle k = \lim_{x \rightarrow \infty} \frac{y}{x} ==\lim _{x \rightarrow \infty} \frac{x \ln \left(e+\frac{1}{x-1}\right)}{x}= \lim_{x \rightarrow \infty} \ln\left(e + \frac{1}{x-1}\right) = \ln e = 1 k = x → ∞ lim x y == x → ∞ lim x x ln ( e + x − 1 1 ) = x → ∞ lim ln ( e + x − 1 1 ) = ln e = 1 确定截距 b b b 截距 b b b b = lim x → ∞ ( y − x ) = lim x → ∞ [ x ln ( e + 1 x − 1 ) − x ] \displaystyle b = \lim_{x \rightarrow \infty} (y - x)= \lim_{x \rightarrow \infty} \left[ x \ln\left(e + \frac{1}{x-1}\right) - x \right] b = x → ∞ lim ( y − x ) = x → ∞ lim [ x ln ( e + x − 1 1 ) − x ] = 提出 x lim x → ∞ x [ ln ( e + 1 x − 1 ) − 1 ] = 1 = ln e lim x → ∞ x [ ln ( e + 1 x − 1 ) − ln e ] = 减法变除法 lim x → ∞ x ln ( 1 + 1 e ( x − 1 ) ) \displaystyle \xlongequal[]{\text{提出}x}\lim _{x \rightarrow \infty} x\left[\ln \left(e+\frac{1}{x-1}\right)-1\right]\xlongequal[]{1=\ln e}\lim _{x \rightarrow \infty} x\left[\ln \left(e+\frac{1}{x-1}\right)-\ln e\right]\xlongequal[]{\text{减法变除法}}\lim _{x \rightarrow \infty} x \ln \left(1+\frac{1}{\mathrm{e}(x-1)}\right) 提出 x x → ∞ lim x [ ln ( e + x − 1 1 ) − 1 ] 1 = l n e x → ∞ lim x [ ln ( e + x − 1 1 ) − ln e ] 减法变除法 x → ∞ lim x ln ( 1 + e ( x − 1 ) 1 ) = ln ( 1 + x ~ x ) lim x → ∞ x e ( x − 1 ) = 分子分母的 x 消去 1 e \displaystyle \xlongequal[]{\ln (1+x\text{~}x)}\lim _{x \rightarrow \infty} \frac{x}{\mathrm{e}(x-1)}\xlongequal[]{\text{分子分母的}x\text{消去}}\frac{1}{\mathrm{e}} l n ( 1 + x ~ x ) x → ∞ lim e ( x − 1 ) x 分子分母的 x 消去 e 1 斜渐近线方程 结合斜率 k k k b b b y = k x + b = x + 1 e y = kx + b= x + \frac{1}{e} y = k x + b = x + e 1 y = x + 1 e y = x + \frac{1}{e} y = x + e 1 (2) 若微分方程 y ′ ′ + a y ′ + b y = 0 y^{\prime \prime}+a y^{\prime}+b y=0 y ′′ + a y ′ + b y = 0 ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) a < 0 , b > 0 a<0, b>0 a < 0 , b > 0 a > 0 , b > 0 a>0, b>0 a > 0 , b > 0 a = 0 , b > 0 a=0, b>0 a = 0 , b > 0 a = 0 , b < 0 a=0, b<0 a = 0 , b < 0 关于二阶常系数齐次线性微分方程 y ′ ′ + p y ′ + q y = 0 \displaystyle y'' + p y' + q y = 0 y ′′ + p y ′ + q y = 0 写出特征方程 λ 2 + p λ + q = 0 \displaystyle \lambda^2 + p\lambda + q = 0 λ 2 + p λ + q = 0 求出特征方程的两个根 λ 1 , λ 2 \displaystyle \lambda_1, \lambda_2 λ 1 , λ 2 根据特征方程两个根的不同情形,通解如下: 特征方程 λ 2 + p λ + q = 0 \displaystyle \lambda^2 + p\lambda + q = 0 λ 2 + p λ + q = 0 微分方程 y ′ ′ + p y ′ + q y = 0 \displaystyle y'' + p y' + q y = 0 y ′′ + p y ′ + q y = 0 两个不同实根 λ 1 , λ 2 \displaystyle \lambda_1, \lambda_2 λ 1 , λ 2 y = C 1 e λ 1 x + C 2 e λ 2 x \displaystyle y = C_1 e^{\lambda_1 x} + C_2 e^{\lambda_2 x} y = C 1 e λ 1 x + C 2 e λ 2 x 两个相同实根 λ 1 = λ 2 \displaystyle \lambda_1 = \lambda_2 λ 1 = λ 2 y = ( C 1 + C 2 x ) e λ 1 x \displaystyle y = (C_1 + C_2 x) e^{\lambda_1 x} y = ( C 1 + C 2 x ) e λ 1 x 一对共轭复根 λ 1 , 2 = α ± β i \displaystyle \lambda_{1, 2} = \alpha \pm \beta i λ 1 , 2 = α ± β i y = e α x ( C 1 cos β x + C 2 sin β x ) \displaystyle y = e^{\alpha x}(C_1 \cos \beta x + C_2 \sin \beta x) y = e αx ( C 1 cos β x + C 2 sin β x )
判断无界的条件 lim x → − ∞ e λ x = { 0 λ > 0 + ∞ λ < 0 \displaystyle \lim _{x \rightarrow-\infty} e^{\lambda x}=\left\{\begin{array}{cc}0 & \lambda>0 \\+\infty & \lambda<0\end{array}\right. x → − ∞ lim e λ x = { 0 + ∞ λ > 0 λ < 0 lim x → + ∞ e λ x = { + ∞ λ > 0 0 λ < 0 \displaystyle \lim _{x \rightarrow+\infty} e^{\lambda x}=\left\{\begin{array}{cl}+\infty & \lambda>0 \\0 & \lambda<0\end{array}\right. x → + ∞ lim e λ x = { + ∞ 0 λ > 0 λ < 0 则λ = 0 \lambda=0 λ = 0 当微分方程 y ′ ′ + a y ′ + b y = 0 y^{\prime \prime}+a y^{\prime}+b y=0 y ′′ + a y ′ + b y = 0 r 2 + a r + b = 0 r^2+a r+b=0 r 2 + a r + b = 0 有实根时, a 2 − 4 b ⩾ 0 a^2-4 b \geqslant 0 a 2 − 4 b ⩾ 0 r 1 , r 2 r_1, r_2 r 1 , r 2 当r 1 ≠ r 2 r_1\neq r_2 r 1 = r 2 y = C 1 e r 1 x ⏟ ∞ + C 2 e r 1 x ( r 1 ≠ r 2 ) y=\underbrace{C_1 \mathrm{e}^{r_1 x}}_{\infty}+C_2 \mathrm{e}^{r_1 x}\left(r_1 \neq r_2\right) y = ∞ C 1 e r 1 x + C 2 e r 1 x ( r 1 = r 2 ) ( − ∞ (-\infty ( − ∞ + ∞ ) +\infty) + ∞ ) 取 C 1 = C 2 = 1 \displaystyle C_1 = C_2 = 1 C 1 = C 2 = 1 lim x → − ∞ ( e λ 1 x + e λ 2 x ) \displaystyle \lim_{x \to -\infty} (e^{\lambda_1 x} + e^{\lambda_2 x}) x → − ∞ lim ( e λ 1 x + e λ 2 x ) lim x → + ∞ ( e λ 1 x + e λ 2 x ) \displaystyle \lim_{x \to +\infty} (e^{\lambda_1 x} + e^{\lambda_2 x}) x → + ∞ lim ( e λ 1 x + e λ 2 x ) ∞ \displaystyle \infty ∞ 当r 1 = r 2 r_1=r_2 r 1 = r 2 y = ( C 1 + C 2 x ) e r 1 x ( r 1 = r 2 ) y=\left(C_1+C_2 x\right) \mathrm{e}^{r_1 x}\left(r_1=r_2\right) y = ( C 1 + C 2 x ) e r 1 x ( r 1 = r 2 ) ( − ∞ (-\infty ( − ∞ + ∞ ) +\infty) + ∞ ) 取 C 1 = 0 \displaystyle C_1 = 0 C 1 = 0 C 2 = 1 \displaystyle C_2 = 1 C 2 = 1 lim x → − ∞ x e λ x \displaystyle \lim_{x \to -\infty} x e^{\lambda x} x → − ∞ lim x e λ x lim x → + ∞ x e λ x \displaystyle \lim_{x \to +\infty} x e^{\lambda x} x → + ∞ lim x e λ x ∞ \displaystyle \infty ∞ 当 a 2 − 4 b < 0 a^2-4 b<0 a 2 − 4 b < 0 α + β i \alpha+\beta \mathrm{i} α + β i y = ( C 1 cos β x + C 2 sin β x ) e α y=\left(C_1 \cos \beta x+C_2 \sin \beta x\right) \mathrm{e}^\alpha y = ( C 1 cos β x + C 2 sin β x ) e α 对于 α ≠ 0 \displaystyle \alpha \neq 0 α = 0 C 1 = 1 \displaystyle C_1 = 1 C 1 = 1 C 2 = 0 \displaystyle C_2 = 0 C 2 = 0 y = e α x cos β x \displaystyle y = e^{\alpha x} \cos \beta x y = e αx cos β x ( − ∞ , + ∞ ) \displaystyle (-\infty, +\infty) ( − ∞ , + ∞ ) 对于 α = 0 \displaystyle \alpha = 0 α = 0 y = C 1 cos β x + C 2 sin β x \displaystyle y = C_1 \cos \beta x + C_2 \sin \beta x y = C 1 cos β x + C 2 sin β x C 1 , C 2 \displaystyle C_1, C_2 C 1 , C 2 ( − ∞ , + ∞ ) \displaystyle (-\infty, +\infty) ( − ∞ , + ∞ ) 若想解在 ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) α = 0 \alpha=0 α = 0 a = − α 2 a=-\frac{\alpha}{2} a = − 2 α a = 0 a=0 a = 0 结合 a 2 − 4 b < 0 a^2-4 b<0 a 2 − 4 b < 0 b > 0 b>0 b > 0 (3) 设函数 y = f ( x ) y=f(x) y = f ( x ) { x = 2 t + ∣ t ∣ , y = ∣ t ∣ sin t \displaystyle \left\{\begin{array}{l}x=2 t+|t|, \\ y=|t| \sin t\end{array}\right. { x = 2 t + ∣ t ∣ , y = ∣ t ∣ sin t f ( x ) f(x) f ( x ) f ′ ( 0 ) f^{\prime}(0) f ′ ( 0 ) f ′ ( 0 ) f^{\prime}(0) f ′ ( 0 ) f ′ ( x ) f^{\prime}(x) f ′ ( x ) x = 0 x=0 x = 0 f ′ ( x ) f^{\prime}(x) f ′ ( x ) f ′ ′ ( 0 ) f^{\prime \prime}(0) f ′′ ( 0 ) f ′ ′ ( 0 ) f^{\prime \prime}(0) f ′′ ( 0 ) f ′ ′ ( x ) f^{\prime \prime}(x) f ′′ ( x ) x = 0 x=0 x = 0
读题分别问你子孙三代 f ( x ) f(x) f ( x ) f ′ ( 0 ) f^{\prime}(0) f ′ ( 0 ) f ′ ( 0 ) f^{\prime}(0) f ′ ( 0 ) f ′ ( x ) f^{\prime}(x) f ′ ( x ) x = 0 x=0 x = 0 f ′ ( x ) f^{\prime}(x) f ′ ( x ) f ′ ′ ( 0 ) f^{\prime \prime}(0) f ′′ ( 0 ) f ′ ′ ( 0 ) f^{\prime \prime}(0) f ′′ ( 0 ) f ′ ′ ( x ) f^{\prime \prime}(x) f ′′ ( x ) x = 0 x=0 x = 0 函数 y = f ( x ) y=f(x) y = f ( x ) { x = 2 t + ∣ t ∣ , y = ∣ t ∣ sin t \displaystyle \left\{\begin{array}{l}x=2 t+|t|, \\ y=|t| \sin t\end{array}\right. { x = 2 t + ∣ t ∣ , y = ∣ t ∣ sin t 当 t ⩾ 0 t \geqslant 0 t ⩾ 0 { x = 3 t , y = t sin t , \displaystyle \left\{\begin{array}{l}x=3 t, \\ y=t \sin t,\end{array}\right. { x = 3 t , y = t sin t , x ⩾ 0 , y = x 3 sin x 3 x \geqslant 0, y=\frac{x}{3} \sin \frac{x}{3} x ⩾ 0 , y = 3 x sin 3 x 当 t < 0 t<0 t < 0 { x = t , y = − t sin t , \displaystyle \left\{\begin{array}{l}x=t, \\ y=-t \sin t,\end{array}\right. { x = t , y = − t sin t , x < 0 , y = − x sin x x<0, y=-x \sin x x < 0 , y = − x sin x f ( x ) f^{}(x) f ( x ) f ( x ) = { x 3 sin x 3 , x ⩾ 0 − x sin x , x < 0 \displaystyle f(x)= \begin{cases}\frac{x}{3} \sin \frac{x}{3}, x \geqslant 0 \\-x \sin x, x<0\end{cases} f ( x ) = { 3 x sin 3 x , x ⩾ 0 − x sin x , x < 0 f ( 0 − ) = f ( 0 + ) = f ( 0 ) = 0 \displaystyle f\left(0^{-}\right)=f\left(0^{+}\right)=f(0)=0 f ( 0 − ) = f ( 0 + ) = f ( 0 ) = 0 f ′ ( 0 ) f^{\prime}(0) f ′ ( 0 ) ⇔ \displaystyle \Leftrightarrow ⇔ f ′ ( 0 − ) = lim x → 0 − f ( x ) − f ( 0 ) x − 0 = lim x → 0 − − sin x x − 0 x − 0 = lim x → 0 − − sin x = 0 \displaystyle f^{\prime}\left(0^{-}\right)=\lim _{x \rightarrow 0^{-}} \frac{f(x)-f(0)}{x-0}=\lim _{x \rightarrow 0^{-}} \frac{\frac{-\sin x}{x}-0}{x-0}=\lim _{x \rightarrow 0^{-}}-\sin x=0 f ′ ( 0 − ) = x → 0 − lim x − 0 f ( x ) − f ( 0 ) = x → 0 − lim x − 0 x − s i n x − 0 = x → 0 − lim − sin x = 0 f ′ ( 0 + ) = lim x → 0 + f ( x ) − f ( 0 ) x = lim x → 0 + x 3 sin x 3 − 0 x − 0 = lim x → 0 + 1 3 sin x 3 = 0 \displaystyle f^{\prime}\left(0^{+}\right)=\lim _{x \rightarrow 0^{+}} \frac{f(x)-f(0)}{x}=\lim _{x \rightarrow 0^{+}} \frac{\frac{x}{3} \sin \frac{x}{3}-0}{x-0}=\lim _{x \rightarrow 0^{+}} \frac{1}{3} \sin \frac{x}{3}=0 f ′ ( 0 + ) = x → 0 + lim x f ( x ) − f ( 0 ) = x → 0 + lim x − 0 3 x sin 3 x − 0 = x → 0 + lim 3 1 sin 3 x = 0 f ′ ( 0 − ) = f ′ ( 0 + ) = 0 \displaystyle f^{\prime}\left(0^{-}\right)=f^{\prime}\left(0^{+}\right)=0 f ′ ( 0 − ) = f ′ ( 0 + ) = 0 f ′ ( 0 ) f^{\prime}(0) f ′ ( 0 ) 判断f ′ ( x ) f'(x) f ′ ( x ) 可导必然连续,这一步是否多余 ) x > 0 , f ′ ( x ) = 1 3 sin x 3 + x 9 cos x 3 → x → 0 + lim x → 0 + f ′ ( x ) = 0 \displaystyle x>0, f^{\prime}(x)=\frac{1}{3} \sin \frac{x}{3}+\frac{x}{9} \cos \frac{x}{3} \xrightarrow{x \rightarrow 0^{+}} \lim _{x \rightarrow 0^{+}} f^{\prime}(x)=0 x > 0 , f ′ ( x ) = 3 1 sin 3 x + 9 x cos 3 x x → 0 + x → 0 + lim f ′ ( x ) = 0 x < 0 , f ′ ( x ) = − sin x − x cos x → x → 0 − lim x → 0 − f ′ ( x ) = 0 \displaystyle x<0, f^{\prime}(x)=-\sin x-x \cos x \quad \xrightarrow{x \rightarrow 0^{-}} \lim _{x \rightarrow 0^{-}} f^{\prime}(x)=0 x < 0 , f ′ ( x ) = − sin x − x cos x x → 0 − x → 0 − lim f ′ ( x ) = 0 lim x → 0 + f ′ ( x ) = lim x → 0 − f ′ ( x ) = f ′ ( 0 ) = 0 \displaystyle \lim _{x \rightarrow 0^{+}} f^{\prime}(x)=\lim _{x \rightarrow 0^{-}} f^{\prime}(x)=f^{\prime}(0)=0 x → 0 + lim f ′ ( x ) = x → 0 − lim f ′ ( x ) = f ′ ( 0 ) = 0 判断f ′ ′ ( x ) f''(x) f ′′ ( x ) f ′ ′ ( 0 + ) = lim x → 0 + f ′ ( x ) − f ′ ( 0 ) x − 0 = lim x → 0 + 1 3 sin x 3 + x 9 cos x 3 x \displaystyle f^{\prime \prime}\left(0^{+}\right)=\lim _{x \rightarrow 0^{+}} \frac{f^{\prime}(x)-f^{\prime}(0)}{x-0}=\lim _{x \rightarrow 0^{+}} \frac{\frac{1}{3} \sin \frac{x}{3}+\frac{x}{9} \cos \frac{x}{3}}{x} f ′′ ( 0 + ) = x → 0 + lim x − 0 f ′ ( x ) − f ′ ( 0 ) = x → 0 + lim x 3 1 sin 3 x + 9 x cos 3 x = lim x → 0 + 1 3 ⋅ sin x 3 x + 1 9 ⋅ cos x 3 = lim x → 0 + 1 3 ⋅ x 3 x + 1 9 . \displaystyle =\lim _{x \rightarrow 0^{+}} \frac{1}{3} \cdot \frac{\sin \frac{x}{3}}{x}+\frac{1}{9} \cdot \cos \frac{x}{3}=\lim _{x \rightarrow 0^{+}} \frac{1}{3} \cdot \frac{\frac{x}{3}}{x}+\frac{1}{9} . = x → 0 + lim 3 1 ⋅ x sin 3 x + 9 1 ⋅ cos 3 x = x → 0 + lim 3 1 ⋅ x 3 x + 9 1 . = 1 9 + 1 9 = 2 9 \displaystyle =\frac{1}{9}+\frac{1}{9}=\frac{2}{9} = 9 1 + 9 1 = 9 2 f ′ ′ ( 0 − ) = lim x → 0 − f ′ ( x ) − f ′ ( 0 ) x − 0 = lim x → 0 − − sin x − x cos x x − 0 = − 2 \displaystyle f^{\prime \prime}\left(0^{-}\right)=\lim _{x \rightarrow 0^{-}} \frac{f^{\prime}(x)-f^{\prime}(0)}{x-0}=\lim _{x \rightarrow 0^{-}} \frac{-\sin x-x \cos x}{x-0}=-2 f ′′ ( 0 − ) = x → 0 − lim x − 0 f ′ ( x ) − f ′ ( 0 ) = x → 0 − lim x − 0 − sin x − x cos x = − 2 f ′ ′ ( 0 + ) ≠ f ′ ′ ( 0 − ) \displaystyle f^{\prime \prime}\left(0^{+}\right) \neq f^{\prime \prime}\left(0^{-}\right) f ′′ ( 0 + ) = f ′′ ( 0 − ) f ′ ′ ( 0 ) f^{\prime \prime}(0) f ′′ ( 0 ) (4) 已知 a n < b n ( n = 1 , 2 , ⋯ ) a_{n}<b_{n}(n=1,2, \cdots) a n < b n ( n = 1 , 2 , ⋯ ) ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_{n} n = 1 ∑ ∞ a n ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_{n} n = 1 ∑ ∞ b n ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_{n} n = 1 ∑ ∞ a n ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_{n} n = 1 ∑ ∞ b n
笠应选 A. 正向级数 交错级数 由级数 ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_n n = 1 ∑ ∞ a n ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_n n = 1 ∑ ∞ b n a n < b n a_n<b_n a n < b n 可以推出 ∑ ∞ ∣ a n − b n ∣ \displaystyle \sum^{\infty}\left|a_n-b_n\right| ∑ ∞ ∣ a n − b n ∣ 若 ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_n n = 1 ∑ ∞ b n 由 ∣ a n ∣ = ∣ a n − b n + b n ∣ → ∣ a ± b ∣ ⩽ ∣ a ∣ + ∣ b ∣ ⩽ ∣ a n − b n ∣ + ∣ b n ∣ \left|a_n\right|=\left|a_n-b_n+b_n\right| \xrightarrow[]{|a \pm b| \leqslant|a|+|b|}\leqslant\left|a_n-b_n\right|+\left|b_n\right| ∣ a n ∣ = ∣ a n − b n + b n ∣ ∣ a ± b ∣ ⩽ ∣ a ∣ + ∣ b ∣ ⩽ ∣ a n − b n ∣ + ∣ b n ∣ → 大的收敛,小的也收敛 \displaystyle \xrightarrow[]{\text{大的收敛,小的也收敛}} 大的收敛,小的也收敛 ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_n n = 1 ∑ ∞ a n 若 ∑ n − 1 ∞ a n \displaystyle \sum_{n-1}^{\infty} a_n n − 1 ∑ ∞ a n 由 ∣ b n ∣ = ∣ b n − a n + a n ∣ → ∣ a ± b ∣ ⩽ ∣ a ∣ + ∣ b ∣ ⩽ ∣ b n − a n ∣ + ∣ a n ∣ \left|b_n\right|=\left|b_n-a_n+a_n\right|\xrightarrow[]{|a \pm b| \leqslant|a|+|b|} \leqslant\left|b_n-a_n\right|+\left|a_n\right| ∣ b n ∣ = ∣ b n − a n + a n ∣ ∣ a ± b ∣ ⩽ ∣ a ∣ + ∣ b ∣ ⩽ ∣ b n − a n ∣ + ∣ a n ∣ → 大的收敛,小的也收敛 \displaystyle \xrightarrow[]{\text{大的收敛,小的也收敛}} 大的收敛,小的也收敛 ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_n n = 1 ∑ ∞ b n 故选 A. (5) 已知 n n n A , B , C \boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C} A , B , C A B C = O , E \boldsymbol{A B C}=\boldsymbol{O}, \boldsymbol{E} ABC = O , E n n n ( O A B E ) , ( A C O E ) , ( E A B A B O ) \displaystyle \left(\begin{array}{cc}\boldsymbol{O} & \boldsymbol{A} \\ \boldsymbol{B} & \boldsymbol{E}\end{array}\right),\left(\begin{array}{cc}\boldsymbol{A} & \boldsymbol{C} \\ \boldsymbol{O} & \boldsymbol{E}\end{array}\right),\left(\begin{array}{cc}\boldsymbol{E} & \boldsymbol{A B} \\ \boldsymbol{A B} & \boldsymbol{O}\end{array}\right) ( O B A E ) , ( A O C E ) , ( E AB AB O ) r 1 r_{1} r 1 r 2 , r 3 r_{2}, r_{3} r 2 , r 3 r 1 ⩽ r 2 ⩽ r 3 r_{1} \leqslant r_{2} \leqslant r_{3} r 1 ⩽ r 2 ⩽ r 3 r 1 ⩽ r 3 ⩽ r 2 r_{1} \leqslant r_{3} \leqslant r_{2} r 1 ⩽ r 3 ⩽ r 2 r 3 ⩽ r 1 ⩽ r 2 r_{3} \leqslant r_{1} \leqslant r_{2} r 3 ⩽ r 1 ⩽ r 2 r 2 ⩽ r 1 ⩽ r 3 r_{2} \leqslant r_{1} \leqslant r_{3} r 2 ⩽ r 1 ⩽ r 3
答应选 B. 分块矩阵的重要公式 (1) r ( A ⋅ A B ) = r ( A ) , r ( A B A ) = r ( A ) r(A \cdot A B)=r(A), r\binom{A}{B A}=r(A) r ( A ⋅ A B ) = r ( A ) , r ( B A A ) = r ( A ) (2) r ( A 0 0 B ) = r ( A ) + r ( B ) = r ( A A B 0 B ) = r ( A 0 B A B ) \displaystyle r\left(\begin{array}{ll}A & 0 \\ 0 & B\end{array}\right)=r(A)+r(B)=r\left(\begin{array}{cc}A & A B \\ 0 & B\end{array}\right)=r\left(\begin{array}{cc}A & 0 \\ B A & B\end{array}\right) r ( A 0 0 B ) = r ( A ) + r ( B ) = r ( A 0 A B B ) = r ( A B A 0 B ) (3) r ( A C 0 B ) ⩾ r ( A ) + r ( B ) \displaystyle r\left(\begin{array}{ll}A & C \\ 0 & B\end{array}\right) \geqslant r(A)+r(B) r ( A 0 C B ) ⩾ r ( A ) + r ( B ) 矩阵的秩:越乘越小,越拼越大,分开加最大r ( A B ) ⩽ r ( A ) r ( B ) ≤ r ( A , B ) ⩽ r ( A ) + r ( B ) \displaystyle r(A B) \leqslant \begin{array}{l}r(A) \\ r(B)\end{array} \leq r(A, B) \leqslant r(A)+r(B) r ( A B ) ⩽ r ( A ) r ( B ) ≤ r ( A , B ) ⩽ r ( A ) + r ( B ) 越乘越小 r ( A B ) ⩽ r ( A ) r(A B) \leqslant r(A) r ( A B ) ⩽ r ( A ) r ( A B ) ⩽ r ( B ) r(A B) \leqslant r(B) r ( A B ) ⩽ r ( B ) 越拼越大:r ( A ) → 上下拼 ≤ r ( A B ) → 左右拼 ≤ r ( A C B 0 ) \displaystyle r(A) \xrightarrow[]{\text{上下拼}}\leq r\binom{A}{B} \xrightarrow[]{\text{左右拼}}\leq r\left(\begin{array}{ll}A C \\ B 0\end{array}\right) r ( A ) 上下拼 ≤ r ( B A ) 左右拼 ≤ r ( A C B 0 ) 舒尔公式:用E去消0 ( 0 A B C E ) → r 1 + ( − A ) r 2 ( − A B C 0 B C E ) → c 1 + c 2 ⋅ ( − B C ) ( − A B C 0 0 E ) \displaystyle \left(\begin{array}{cc} 0 A \\ BC E \end{array}\right) \xrightarrow{r_1 + (-A) r_2} \left(\begin{array}{cc} -ABC 0 \\ BC E \end{array}\right) \xrightarrow{c_1 + c_2 \cdot (-BC)} \left(\begin{array}{cc} -ABC 0 \\ 0 E \end{array}\right) ( 0 A BCE ) r 1 + ( − A ) r 2 ( − A BC 0 BCE ) c 1 + c 2 ⋅ ( − BC ) ( − A BC 0 0 E ) r ( A B C ) = 0 , r = n \displaystyle r(ABC) = 0, \, r = n r ( A BC ) = 0 , r = n ( A B C 0 E ) → r 1 + ( − C ) r 2 ( A B 0 0 E ) \displaystyle \left(\begin{array}{ll} AB C \\ 0 E \end{array}\right) \xrightarrow{r_1 + (-C) r_2} \left(\begin{array}{ll} AB 0 \\ 0 E \end{array}\right) ( A BC 0 E ) r 1 + ( − C ) r 2 ( A B 0 0 E ) r 2 = r ( A B ) + r ( E ) = r ( A B ) + n \displaystyle r_2 = r(AB) + r(E) = r(AB) + n r 2 = r ( A B ) + r ( E ) = r ( A B ) + n ( E A B A B 0 ) → r 2 + ( − A B ) r 1 ( E A B 0 ) → c 2 + ( − A B ) c 1 ( E 0 ) \displaystyle \left(\begin{array}{l} EAB \\ AB 0 \end{array}\right) \xrightarrow{r_2 + (-AB) r_1} \left(\begin{array}{c} EAB \\ 0 \end{array}\right) \xrightarrow{c_2 + (-AB) c_1} \left(\begin{array}{c} E \\ 0 \end{array}\right) ( E A B A B 0 ) r 2 + ( − A B ) r 1 ( E A B 0 ) c 2 + ( − A B ) c 1 ( E 0 ) r 3 = n + r ( A B A B ) \displaystyle r_3 = n + r(ABAB) r 3 = n + r ( A B A B ) → 矩阵越乘越小 r 3 < r 2 < r 1 \displaystyle \xrightarrow[]{\text{矩阵越乘越小}}r_3 < r_2 < r_1 矩阵越乘越小 r 3 < r 2 < r 1 (6) 下列矩阵中不能相似于对角矩阵的是( 1 1 a 0 2 2 0 0 3 ) \displaystyle \left(\begin{array}{lll}1 & 1 & a \\ 0 & 2 & 2 \\ 0 & 0 & 3\end{array}\right) 1 0 0 1 2 0 a 2 3 ( 1 1 a 1 2 0 a 0 3 ) \displaystyle \left(\begin{array}{lll}1 & 1 & a \\ 1 & 2 & 0 \\ a & 0 & 3\end{array}\right) 1 1 a 1 2 0 a 0 3 ( 1 1 a 0 2 0 0 0 2 ) \displaystyle \left(\begin{array}{lll}1 & 1 & a \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{array}\right) 1 0 0 1 2 0 a 0 2 ( 1 1 a 0 2 2 0 0 2 ) \displaystyle \left(\begin{array}{lll}1 & 1 & a \\ 0 & 2 & 2 \\ 0 & 0 & 2\end{array}\right) 1 0 0 1 2 0 a 2 2
答 应选 D. n阶方阵A可相似对角化的充分必要条件 A有n个线性无关的特征向量。 对于A的每个特征值 λ i \displaystyle \lambda_i λ i λ i \displaystyle \lambda_i λ i n阶方阵A可相似对角化的充分但不必要条件 A \mathrm{A} A 1 , 2 , 3 1,2,3 1 , 2 , 3 B \mathrm{B} B C \mathrm{C} C ( C − 2 E ) x = 0 ⇒ S = n − r ( C − 2 E ) = 3 − 1 = 2. \displaystyle (C-2 E) x=0 \quad \Rightarrow \quad S=n-r(C-2 E)=3-1=2 . ( C − 2 E ) x = 0 ⇒ S = n − r ( C − 2 E ) = 3 − 1 = 2. ∣ c − 2 E ∣ = ∣ 1 1 a 0 0 0 0 0 0 ∣ \displaystyle |c-2 E|=\left|\begin{array}{lll}1 & 1 & a \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right| ∣ c − 2 E ∣ = 1 0 0 1 0 0 a 0 0 D 中矩阵的特征值 2 为二重根, 其对应的线性无关特征向量个数为 1 , 不可相似对角化 ,故选 D. ( D − 2 E ) x = 0 ⇒ S = n − r ( D − 2 E ) = 3 − 2 = 1 \displaystyle (D-2 E) x=0 \quad \Rightarrow \quad S=n-r(D-2 E)=3-2=1 ( D − 2 E ) x = 0 ⇒ S = n − r ( D − 2 E ) = 3 − 2 = 1 ∣ D − 2 E ∣ = ∣ 1 1 9 0 0 2 0 0 0 ∣ \displaystyle |D-2 E|=\left|\begin{array}{lll}1 & 1 & 9 \\ 0 & 0 & 2 \\ 0 & 0 & 0\end{array}\right| ∣ D − 2 E ∣ = 1 0 0 1 0 0 9 2 0 (7) 已知向量 α 1 = ( 1 2 3 ) , α 2 = ( 2 1 1 ) , β 1 = ( 2 5 9 ) , β 2 = ( 1 0 1 ) \displaystyle \boldsymbol{\alpha}_{1}=\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right), \boldsymbol{\alpha}_{2}=\left(\begin{array}{l}2 \\ 1 \\ 1\end{array}\right), \boldsymbol{\beta}_{1}=\left(\begin{array}{l}2 \\ 5 \\ 9\end{array}\right), \boldsymbol{\beta}_{2}=\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right) α 1 = 1 2 3 , α 2 = 2 1 1 , β 1 = 2 5 9 , β 2 = 1 0 1 γ \boldsymbol{\gamma} γ α 1 , α 2 \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2} α 1 , α 2 β 1 , β 2 \boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2} β 1 , β 2 γ = \boldsymbol{\gamma}= γ = k ( 3 3 4 ) , k ∈ R \displaystyle k\left(\begin{array}{l}3 \\ 3 \\ 4\end{array}\right), k \in \mathbf{R} k 3 3 4 , k ∈ R k ( 3 5 10 ) , k ∈ R \displaystyle k\left(\begin{array}{c}3 \\ 5 \\ 10\end{array}\right), k \in \mathbf{R} k 3 5 10 , k ∈ R k ( − 1 1 2 ) , k ∈ R \displaystyle k\left(\begin{array}{c}-1 \\ 1 \\ 2\end{array}\right), k \in \mathbf{R} k − 1 1 2 , k ∈ R k ( 1 5 8 ) , k ∈ R \displaystyle k\left(\begin{array}{l}1 \\ 5 \\ 8\end{array}\right), k \in \mathbf{R} k 1 5 8 , k ∈ R
代入法 ( α 1 , α 2 , y ) = ( 1 2 1 2 1 5 3 1 8 ) → r 3 − 3 r 1 r 2 − 2 r 1 ( 1 2 1 0 − 3 3 0 − 5 5 ) ⟶ ( 1 2 1 0 1 − 1 0 0 0 ) \displaystyle \left(\alpha_1, \alpha_2, y\right)=\left(\begin{array}{ll:l}1 & 2 & 1 \\ 2 & 1 & 5 \\ 3 & 1 & 8\end{array}\right) \xrightarrow[r_3-3 r_1]{r_2-2 r_1}\left(\begin{array}{cc:c}1 & 2 & 1 \\ 0 & -3 & 3 \\ 0 & -5 & 5\end{array}\right) \longrightarrow\left(\begin{array}{cc:c}1 & 2 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 0\end{array}\right) ( α 1 , α 2 , y ) = 1 2 3 2 1 1 1 5 8 r 2 − 2 r 1 r 3 − 3 r 1 1 0 0 2 − 3 − 5 1 3 5 ⟶ 1 0 0 2 1 0 1 − 1 0 γ \gamma γ α 1 , α 2 \alpha_1, \alpha_2 α 1 , α 2 ( β 2 , β 1 , γ ) = ( 1 2 1 0 5 5 1 9 8 ) → ( 1 2 1 0 5 5 0 7 7 ) → ( 1 2 1 0 1 1 0 0 0 ) \displaystyle \left(\beta_2, \beta_1, \gamma\right)=\left(\begin{array}{ll:l}1 & 2 & 1 \\ 0 & 5 & 5 \\ 1 & 9 & 8\end{array}\right) \rightarrow\left(\begin{array}{ll:l}1 & 2 & 1 \\ 0 & 5 & 5 \\ 0 & 7 & 7\end{array}\right) \rightarrow\left(\begin{array}{ll:l}1 & 2 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0\end{array}\right) ( β 2 , β 1 , γ ) = 1 0 1 2 5 9 1 5 8 → 1 0 0 2 5 7 1 5 7 → 1 0 0 2 1 0 1 1 0 γ \gamma γ β 2 , β 1 , \beta_2, \beta_1, β 2 , β 1 , 直接算 若 γ \boldsymbol{\gamma} γ α 1 , α 2 \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2} α 1 , α 2 β 1 , β 2 \boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2} β 1 , β 2 ∃ x 1 , x 2 , x 3 , x 4 , \displaystyle \exists x_1, x_2, x_3, x_4, ∃ x 1 , x 2 , x 3 , x 4 , γ = x 1 α 1 + x 2 α 2 = x 3 β 1 + x 4 β 2 \gamma=x_1 \alpha_1+x_2 \alpha_2=x_3 \beta_1+x_4 \beta_2 γ = x 1 α 1 + x 2 α 2 = x 3 β 1 + x 4 β 2 → 移项整理 x 1 α 1 + x 2 α 2 − x 3 β 1 − x 4 β 2 = 0 \displaystyle \xrightarrow[]{\text{移项整理}}x_1\alpha_1+x_2 \alpha_2-x_3 \beta_1-x_4 \beta_2=0 移项整理 x 1 α 1 + x 2 α 2 − x 3 β 1 − x 4 β 2 = 0 → 提出 x ( α 1 , α 2 , − β 1 , − β 2 ) x = 0 \displaystyle \xrightarrow[]{\text{提出}x} \left(\alpha_1, \alpha_2,-\beta_1,-\beta_2\right) x=0 \quad 提出 x ( α 1 , α 2 , − β 1 , − β 2 ) x = 0 ( 1 2 − 2 − 1 2 1 − 5 0 3 1 − 9 − 1 ) → r 2 − 2 r 1 r 3 − 3 r 1 ( 1 2 − 2 − 1 0 − 3 − 1 2 0 − 5 − 3 2 ) → r 3 ⋅ ( − 3 4 ) { r 3 − 5 3 r 2 r 2 ⋅ ( − 1 ) ( 1 2 − 2 − 1 0 3 1 − 2 0 0 1 1 ) \displaystyle \left(\begin{array}{cccc}1 & 2 & -2 & -1 \\ 2 & 1 & -5 & 0 \\ 3 & 1 & -9 & -1\end{array}\right) \xrightarrow[]{\begin{aligned}& r_2-2 r_1 \\& r_3-3 r_1\end{aligned}}\left(\begin{array}{cccc}1 & 2 & -2 & -1 \\ 0 & -3 & -1 & 2 \\ 0 & -5 & -3 & 2\end{array}\right) \xrightarrow[r_3 \cdot\left(-\frac{3}{4}\right)]{\left\{\begin{array}{l} r_3-\frac{5}{3} r_2\\r_2 \cdot(-1) \\ \end{array}\right.}\left(\begin{array}{cccc}1 & 2 & -2 & -1 \\ 0 & 3 & 1 & -2 \\ 0 & 0 & 1 & 1\end{array}\right) 1 2 3 2 1 1 − 2 − 5 − 9 − 1 0 − 1 r 2 − 2 r 1 r 3 − 3 r 1 1 0 0 2 − 3 − 5 − 2 − 1 − 3 − 1 2 2 { r 3 − 3 5 r 2 r 2 ⋅ ( − 1 ) r 3 ⋅ ( − 4 3 ) 1 0 0 2 3 0 − 2 1 1 − 1 − 2 1 { → 化为方程组求通解 x 1 + 2 x 2 − 2 x 3 − x 4 = 0 3 x 2 + x 3 − 2 x 4 = 0 x 3 + x 4 = 0 \displaystyle \left\{\begin{aligned}\xrightarrow[]{\text{化为方程组求通解}} x_1+2 x_2-2 x_3-x_4 & =0 \\ 3 x_2+x_3-2 x_4 & =0 \\ x_3+x_4 & =0\end{aligned} \right. ⎩ ⎨ ⎧ 化为方程组求通解 x 1 + 2 x 2 − 2 x 3 − x 4 3 x 2 + x 3 − 2 x 4 x 3 + x 4 = 0 = 0 = 0 → x 4 为自由元 { x 1 = − 3 k x 2 = k x 3 = − k x 4 = k ⇒ x = ( x 1 x 2 x 3 x 4 ) = ( − 3 k k − k k ) k ∈ R \displaystyle \xrightarrow[]{x_4\text{为自由元}}\left\{\begin{array}{l}x_1=-3 k \\ x_2=k \\ x_3=-k \\ x_4=k\end{array} \Rightarrow x=\left(\begin{array}{l}x_1 \\ x_2 \\ x_3 \\ x_4\end{array}\right)=\left(\begin{array}{c}-3 k \\ k \\ -k \\ k\end{array}\right) k \in R\right. x 4 为自由元 ⎩ ⎨ ⎧ x 1 = − 3 k x 2 = k x 3 = − k x 4 = k ⇒ x = x 1 x 2 x 3 x 4 = − 3 k k − k k k ∈ R 将( x 1 x 2 ) = ( − 3 k k ) \binom{x_1}{x_2}=\binom{-3 k}{k} ( x 2 x 1 ) = ( k − 3 k ) y = x 1 α 1 + x 2 α 2 y=x_1 \alpha_1+x_2 \alpha_2 y = x 1 α 1 + x 2 α 2 y = − 3 k ( 1 2 3 ) + k ( 2 1 1 ) = ( − k − 5 k − 8 k ) = k ( − 1 − 5 − 8 ) = k ( 1 5 8 ) \displaystyle y=-3 k\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)+k\left(\begin{array}{l}2 \\ 1 \\ 1\end{array}\right)=\left(\begin{array}{c}-k \\ -5 k \\ -8 k\end{array}\right)=k\left(\begin{array}{l}-1 \\ -5 \\ -8\end{array}\right)=k\left(\begin{array}{l}1 \\ 5 \\ 8\end{array}\right) y = − 3 k 1 2 3 + k 2 1 1 = − k − 5 k − 8 k = k − 1 − 5 − 8 = k 1 5 8 (8) 设随机变量 X X X E ( ∣ X − E X ∣ ) = E(|X-E X|)= E ( ∣ X − EX ∣ ) = 1 e \frac{1}{\mathrm{e}} e 1 1 2 \frac{1}{2} 2 1 2 e \frac{2}{\mathrm{e}} e 2
答 应选 C. 泊松分布的分布律与数字特征 若随机变量 X X X λ \lambda λ X ∼ P ( λ ) X \sim P(\lambda) X ∼ P ( λ ) 分布律P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2 , ⋯ \displaystyle P\{X=k\}=\frac{\lambda^k \mathrm{e}^{-\lambda}}{k!}, k=0,1,2, \cdots P { X = k } = k ! λ k e − λ , k = 0 , 1 , 2 , ⋯ λ > 0 \lambda>0 λ > 0 期望 E ( X ) = λ E(X)=\lambda E ( X ) = λ 方差D ( X ) = λ D(X)=\lambda D ( X ) = λ E ( ∣ X − E X ∣ ) = 泊松分布 E X = 1 E ∣ X − 1 ∣ → 去掉绝对值 E(|X-E X|)\xlongequal[\text{泊松分布}]{EX=1}E|X-1|\xrightarrow[]{\text{去掉绝对值}} E ( ∣ X − EX ∣ ) EX = 1 泊松分布 E ∣ X − 1∣ 去掉绝对值 E ∣ X − 1 ∣ = 颗粒感 : 函数的期望 P { X = k } = λ k e − λ k ! ∑ k = 0 ∞ ∣ k − 1 ∣ ⋅ e − 1 k ! \displaystyle E|X-1| \xlongequal[\text{颗粒感}:\text{函数的期望}]{P\{X=k\}=\frac{\lambda^k \mathrm{e}^{-\lambda}}{k!}}\sum_{k=0}^{\infty} |k-1| \cdot \frac{e^{-1}}{k!} E ∣ X − 1∣ P { X = k } = k ! λ k e − λ 颗粒感 : 函数的期望 k = 0 ∑ ∞ ∣ k − 1∣ ⋅ k ! e − 1 ∣ x − 1 ∣ = { 1 − x , x = 0 x − 1 x ⩾ 1 \displaystyle |x-1|= \begin{cases}1-x, & x=0 \\ x-1 & x \geqslant 1\end{cases} ∣ x − 1∣ = { 1 − x , x − 1 x = 0 x ⩾ 1 = 把绝对值的 0 单独拆出来 e − 1 0 ! + ∑ k = 1 ∞ ( k − 1 ) ⋅ e − 1 k ! ⏟ 计算方法 : 拆 + 期望 \displaystyle \xlongequal[]{\text{把绝对值的}0\text{单独拆出来}}\frac{e^{-1}}{0!} + \underbrace{\sum_{k=1}^{\infty} (k-1) \cdot \frac{e^{-1}}{k!}}_{\text{计算方法}:\text{拆}+\text{期望}} 把绝对值的 0 单独拆出来 0 ! e − 1 + 计算方法 : 拆 + 期望 k = 1 ∑ ∞ ( k − 1 ) ⋅ k ! e − 1 = e − 1 0 ! + ∑ k = 0 ∞ ( k − 1 ) ⋅ e − 1 k ! − ( 0 − 1 ) ⋅ e − 1 0 ! ⏟ ∑ k = 1 ∞ \displaystyle = \frac{e^{-1}}{0!} + \underbrace{\sum_{k=0}^{\infty} (k-1) \cdot \frac{e^{-1}}{k!} - (0-1) \cdot \frac{e^{-1}}{0!}}_{\sum_{k=1}^{\infty} } = 0 ! e − 1 + ∑ k = 1 ∞ k = 0 ∑ ∞ ( k − 1 ) ⋅ k ! e − 1 − ( 0 − 1 ) ⋅ 0 ! e − 1 = e − 1 + E ( X − 1 ) + e − 1 = E ( X − 1 ) = E X − 1 = 0 2 e − 1 \displaystyle = e^{-1} + E(X-1) + e^{-1} \xlongequal[]{E(X-1)=E X-1=0}2e^{-1} = e − 1 + E ( X − 1 ) + e − 1 E ( X − 1 ) = EX − 1 = 0 2 e − 1 故选 C. (9) 设 X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n N ( μ 1 , σ 2 ) \displaystyle N\left(\mu_{1}, \sigma^{2}\right) N ( μ 1 , σ 2 ) Y 1 , Y 2 , ⋯ , Y m Y_{1}, Y_{2}, \cdots, Y_{m} Y 1 , Y 2 , ⋯ , Y m N ( μ 2 , 2 σ 2 ) \displaystyle N\left(\mu_{2}, 2 \sigma^{2}\right) N ( μ 2 , 2 σ 2 ) X ˉ = 1 n ∑ i = 1 n X i , Y ˉ = 1 m ∑ i = 1 m Y i , S 1 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 , S 2 2 = 1 m − 1 ∑ i = 1 m ( Y i − Y ˉ ) 2 \displaystyle \bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}, \bar{Y}=\frac{1}{m} \sum_{i=1}^{m} Y_{i}, S_{1}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}, S_{2}^{2}=\frac{1}{m-1} \sum_{i=1}^{m}\left(Y_{i}-\bar{Y}\right)^{2} X ˉ = n 1 i = 1 ∑ n X i , Y ˉ = m 1 i = 1 ∑ m Y i , S 1 2 = n − 1 1 i = 1 ∑ n ( X i − X ˉ ) 2 , S 2 2 = m − 1 1 i = 1 ∑ m ( Y i − Y ˉ ) 2 S 1 2 S 2 2 ∼ F ( n , m ) \frac{S_{1}^{2}}{S_{2}^{2}} \sim F(n, m) S 2 2 S 1 2 ∼ F ( n , m ) S 1 2 S 2 2 ∼ F ( n − 1 , m − 1 ) \frac{S_{1}^{2}}{S_{2}^{2}} \sim F(n-1, m-1) S 2 2 S 1 2 ∼ F ( n − 1 , m − 1 ) 2 S 1 2 S 2 2 ∼ F ( n , m ) \frac{2 S_{1}^{2}}{S_{2}^{2}} \sim F(n, m) S 2 2 2 S 1 2 ∼ F ( n , m ) 2 S 1 2 S 2 2 ∼ F ( n − 1 , m − 1 ) \frac{2 S_{1}^{2}}{S_{2}^{2}} \sim F(n-1, m-1) S 2 2 2 S 1 2 ∼ F ( n − 1 , m − 1 )
答 应选 D. 正态总体的抽样分布定理: 设总体 X ∼ N ( μ , σ 2 ) \displaystyle X \sim N(\mu, \sigma^2) X ∼ N ( μ , σ 2 ) X 1 , X 2 , … , X n \displaystyle X_1, X_2, \ldots, X_n X 1 , X 2 , … , X n X \displaystyle X X X ˉ = 1 n ∑ i = 1 n X i \displaystyle \bar{X} = \frac{1}{n} \sum_{i=1}^n X_i X ˉ = n 1 i = 1 ∑ n X i S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 \displaystyle S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})^2 S 2 = n − 1 1 i = 1 ∑ n ( X i − X ˉ ) 2 X ˉ ∼ N ( μ , σ 2 n ) \displaystyle \bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) X ˉ ∼ N ( μ , n σ 2 ) ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \displaystyle \frac{(n-1) S^2}{\sigma^2} \sim \chi^2(n-1) σ 2 ( n − 1 ) S 2 ∼ χ 2 ( n − 1 ) X ˉ \displaystyle \bar{X} X ˉ S 2 \displaystyle S^2 S 2 F分布: 设 U ∼ χ 2 ( n 1 ) \displaystyle U \sim \chi^2(n_1) U ∼ χ 2 ( n 1 ) V ∼ χ 2 ( n 2 ) \displaystyle V \sim \chi^2(n_2) V ∼ χ 2 ( n 2 ) U , V \displaystyle U, V U , V F = U / n 1 V / n 2 \displaystyle F = \frac{U/n_1}{V/n_2} F = V / n 2 U / n 1 ( n 1 , n 2 ) \displaystyle (n_1, n_2) ( n 1 , n 2 ) F ∼ F ( n 1 , n 2 ) \displaystyle F \sim F(n_1, n_2) F ∼ F ( n 1 , n 2 ) X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n N ( μ 1 , σ 2 ) \displaystyle N\left(\mu_{1}, \sigma^{2}\right) N ( μ 1 , σ 2 ) Y 1 , Y 2 , ⋯ , Y m Y_{1}, Y_{2}, \cdots, Y_{m} Y 1 , Y 2 , ⋯ , Y m N ( μ 2 , 2 σ 2 ) \displaystyle N\left(\mu_{2}, 2 \sigma^{2}\right) N ( μ 2 , 2 σ 2 ) 由卡方分布构造F分布 样本方差构造卡方分布 ( n − 1 ) S 1 2 σ 2 ∼ χ 2 ( n − 1 ) \displaystyle \frac{(n-1) S_{1}^{2}}{\sigma^2} \sim \chi^2(n-1) σ 2 ( n − 1 ) S 1 2 ∼ χ 2 ( n − 1 ) ( m − 1 ) S 2 2 2 σ 2 ∼ χ 2 ( m − 1 ) \displaystyle \frac{(m-1) S_{2}^{2}}{2\sigma^2} \sim \chi^2(m-1) 2 σ 2 ( m − 1 ) S 2 2 ∼ χ 2 ( m − 1 ) 卡方分布构造F分布 F = U / n 1 V / n 2 = ( n − 1 ) S 1 2 / ( n − 1 ) ( m − 1 ) S 2 2 / ( m − 1 ) = 2 S 1 2 S 2 2 = F ( n − 1 , m − 1 ) \displaystyle F = \frac{U/n_1}{V/n_2} = \frac{(n-1) S_{1}^{2}/(n-1)}{(m-1) S_{2}^{2}/(m-1)} = \frac{2 S_{1}^{2}}{S_{2}^{2}} = F(n-1, m-1) F = V / n 2 U / n 1 = ( m − 1 ) S 2 2 / ( m − 1 ) ( n − 1 ) S 1 2 / ( n − 1 ) = S 2 2 2 S 1 2 = F ( n − 1 , m − 1 ) (10) 设 X 1 , X 2 X_{1}, X_{2} X 1 , X 2 N ( μ , σ 2 ) \displaystyle N\left(\mu, \sigma^{2}\right) N ( μ , σ 2 ) σ ( σ > 0 ) \displaystyle \sigma(\sigma>0) σ ( σ > 0 ) σ ^ = a ∣ X 1 − X 2 ∣ \displaystyle \hat{\sigma}=a\left|X_{1}-X_{2}\right| σ ^ = a ∣ X 1 − X 2 ∣ σ \displaystyle \sigma σ a = a= a = π 2 \frac{\sqrt{\pi}}{2} 2 π 2 π 2 \frac{\sqrt{2 \pi}}{2} 2 2 π π \sqrt{\pi} π 2 π \sqrt{2 \pi} 2 π 一维正态分布 (1) 服从正态分布 N ( μ , σ 2 ) \displaystyle N\left(\mu, \sigma^2\right) N ( μ , σ 2 ) X X X f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , − ∞ < x < + ∞ . \displaystyle f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}}, \quad-\infty<x<+\infty . f ( x ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2 , − ∞ < x < + ∞. (2) 若 X 1 ∼ N ( μ 1 , σ 1 2 ) , X 2 ∼ N ( μ 2 , σ 2 2 ) \displaystyle X_1 \sim N\left(\mu_1, \sigma_1^2\right), \quad X_2 \sim N\left(\mu_2, \sigma_2^2\right) X 1 ∼ N ( μ 1 , σ 1 2 ) , X 2 ∼ N ( μ 2 , σ 2 2 ) X 1 , X 2 X_1, X_2 X 1 , X 2 a 1 , a 2 a_1, a_2 a 1 , a 2 a 1 X 1 + a 2 X 2 ∼ N ( a 1 μ 1 + a 2 μ 2 , a 1 2 σ 1 2 + a 2 2 σ 2 2 ) . \displaystyle a_1 X_1+a_2 X_2 \sim N\left(a_1 \mu_1+a_2 \mu_2, a_1^2 \sigma_1^2+a_2^2 \sigma_2^2\right) . a 1 X 1 + a 2 X 2 ∼ N ( a 1 μ 1 + a 2 μ 2 , a 1 2 σ 1 2 + a 2 2 σ 2 2 ) . 无偏估计 设 θ ^ \hat{\theta} θ ^ θ \theta θ E ( θ ^ ) = θ E(\hat{\theta})=\theta E ( θ ^ ) = θ θ ^ \hat{\theta} θ ^ θ \theta θ X ∼ N ( μ , σ 1 2 ) , Y ∼ N ( μ 1 , σ 2 2 ) \displaystyle X \sim N\left(\mu, \sigma_{1}^{2}\right), \quad Y \sim N\left(\mu_{1}, \sigma_{2}^{2}\right) \quad X ∼ N ( μ , σ 1 2 ) , Y ∼ N ( μ 1 , σ 2 2 ) X X X Y Y Y → 线性组合 a X + b Y ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 ) \displaystyle \xrightarrow[]{\text{线性组合}}aX + bY \sim N\left(a\mu_{1} + b\mu_{2}, a^{2}\sigma_{1}^{2} + b^{2}\sigma_{2}^{2}\right) 线性组合 a X + bY ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 ) 本题 Y = X 1 − X 2 ∼ N ( 0 , 2 σ 2 ) \displaystyle Y = X_{1} - X_{2} \sim N\left(0, 2\sigma^{2}\right) Y = X 1 − X 2 ∼ N ( 0 , 2 σ 2 ) 求正态的概率密度f Y ( y ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 → μ = 0 , σ = 2 σ 1 2 2 σ e − y 2 4 σ 2 \displaystyle f_{Y(y)} = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \xrightarrow{\mu=0, \sigma=\sqrt{2}\sigma} \frac{1}{2\sqrt{2}\sigma} e^{\frac{-y^{2}}{4\sigma^{2}}} f Y ( y ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2 μ = 0 , σ = 2 σ 2 2 σ 1 e 4 σ 2 − y 2 用定义求期望:E ∣ Y ∣ = 何处算积分 何处求概率 ∫ − ∞ + ∞ ∣ y ∣ f Y ( y ) d y \displaystyle E|Y| \xlongequal[\text{何处算积分}]{\text{何处求概率}} \int_{-\infty}^{+\infty} |y| f_{Y(y)} dy E ∣ Y ∣ 何处求概率 何处算积分 ∫ − ∞ + ∞ ∣ y ∣ f Y ( y ) d y = 代入 f ( y ) ∫ − ∞ + ∞ ∣ y ∣ ⋅ 1 2 2 σ ⋅ e − y 2 4 σ 2 d y \displaystyle \xlongequal[]{\text{代入}f(y)} \int_{-\infty}^{+\infty} |y| \cdot \frac{1}{2\sqrt{2}\sigma} \cdot e^{\frac{-y^{2}}{4\sigma^{2}}} dy 代入 f ( y ) ∫ − ∞ + ∞ ∣ y ∣ ⋅ 2 2 σ 1 ⋅ e 4 σ 2 − y 2 d y = 去绝对值 2 ∫ 0 + ∞ y ⋅ 1 2 2 σ ⋅ e − y 2 4 σ 2 d y \displaystyle \xlongequal[]{\text{去绝对值}} 2\int_{0}^{+\infty} y \cdot \frac{1}{2\sqrt{2}\sigma} \cdot e^{\frac{-y^{2}}{4\sigma^{2}}} dy 去绝对值 2 ∫ 0 + ∞ y ⋅ 2 2 σ 1 ⋅ e 4 σ 2 − y 2 d y = 凑 e 的指数的微分的系数 2 ∫ 0 + ∞ 2 y 4 σ 2 ⋅ σ π ⋅ e − y 2 4 σ 2 d y \displaystyle \xlongequal[]{\text{凑}e\text{的指数的微分的系数}}2\int_{0}^{+\infty} \frac{2y}{4\sigma^{2}} \cdot \frac{\sigma}{\sqrt{\pi}} \cdot e^{\frac{-y^{2}}{4\sigma^{2}}} dy 凑 e 的指数的微分的系数 2 ∫ 0 + ∞ 4 σ 2 2 y ⋅ π σ ⋅ e 4 σ 2 − y 2 d y = 凑微分 2 ∫ 0 + ∞ σ π ⋅ e − y 2 4 σ 2 d ( y 2 4 σ 2 ) \displaystyle \xlongequal[]{\text{凑微分}}2\int_{0}^{+\infty} \frac{\sigma}{\sqrt{\pi}} \cdot e^{\frac{-y^{2}}{4\sigma^{2}}} d\left(\frac{y^{2}}{4\sigma^{2}}\right) 凑微分 2 ∫ 0 + ∞ π σ ⋅ e 4 σ 2 − y 2 d ( 4 σ 2 y 2 ) = ∫ e − x d x = − e − x − 2 ⋅ σ π ⋅ e − y 2 4 σ 2 ∣ 0 + ∞ \displaystyle \xlongequal[]{\int e^{-x} d x=-e^{-x}} -2 \cdot \frac{\sigma}{\sqrt{\pi}} \cdot e^{\frac{-y^{2}}{4\sigma^{2}}} \Big|_{0}^{+\infty} ∫ e − x d x = − e − x − 2 ⋅ π σ ⋅ e 4 σ 2 − y 2 0 + ∞ = e − ∞ = 0 , e 0 = 1 − 2 ⋅ σ π ⋅ ( 0 − 1 ) = 负负得正 2 σ π \displaystyle \xlongequal[]{e^{-\infty}=0, e^0=1} -2 \cdot \frac{\sigma}{\sqrt{\pi}} \cdot (0 - 1) \xlongequal[]{\text{负负得正}}\frac{2\sigma}{\sqrt{\pi}} e − ∞ = 0 , e 0 = 1 − 2 ⋅ π σ ⋅ ( 0 − 1 ) 负负得正 π 2 σ a ⋅ E ∣ X 1 − X 2 ∣ = a ⋅ E ∣ Y ∣ = a ⋅ 2 σ π = 6 \displaystyle a \cdot E|X_1 - X_2| = a \cdot E|Y| = a \cdot \frac{2\sigma}{\sqrt{\pi}} = 6 a ⋅ E ∣ X 1 − X 2 ∣ = a ⋅ E ∣ Y ∣ = a ⋅ π 2 σ = 6 a = π 2 \displaystyle a = \frac{\sqrt{\pi}}{2} a = 2 π E ( a ∣ X 1 − X 2 ∣ ) = a E ( ∣ X 1 − X 2 ∣ ) = a ⋅ 2 σ π = σ \displaystyle E\left(a\left|X_1-X_2\right|\right)=a E\left(\left|X_1-X_2\right|\right)=a \cdot \frac{2 \sigma}{\sqrt{\pi}}=\sigma E ( a ∣ X 1 − X 2 ∣ ) = a E ( ∣ X 1 − X 2 ∣ ) = a ⋅ π 2 σ = σ a = π 2 a=\frac{\sqrt{\pi}}{2} a = 2 π X 1 − X 2 ∼ N ( 0 , 2 σ 2 ) \displaystyle X_1-X_2 \sim N\left(0,2 \sigma^2\right) X 1 − X 2 ∼ N ( 0 , 2 σ 2 ) Z = X 1 − X 2 Z=X_1-X_2 Z = X 1 − X 2 E ( ∣ X 1 − X 2 ∣ ) = ∫ − ∞ + ∞ ∣ z ∣ ⋅ 1 2 π 2 σ ⋅ e − z 2 ω 2 d z = 2 ∫ 0 + ∞ z 2 π σ e − x 2 ω 2 d z \displaystyle E\left(\left|X_1-X_2\right|\right) =\int_{-\infty}^{+\infty}|z| \cdot \frac{1}{\sqrt{2 \pi} \sqrt{2} \sigma} \cdot \mathrm{e}^{-\frac{z^2}{\omega^2}} \mathrm{~d} z=2 \int_0^{+\infty} \frac{z}{2 \sqrt{\pi} \sigma} \mathrm{e}^{-\frac{x^2}{\omega^2}} \mathrm{~d} z E ( ∣ X 1 − X 2 ∣ ) = ∫ − ∞ + ∞ ∣ z ∣ ⋅ 2 π 2 σ 1 ⋅ e − ω 2 z 2 d z = 2 ∫ 0 + ∞ 2 π σ z e − ω 2 x 2 d z = 2 1 2 π σ ( − 2 σ 2 ) ∫ 0 + ∞ e − x 2 4 2 d ( − z 2 4 σ 2 ) = − 2 σ π e − z 2 ω 2 ∣ 0 + ∞ = 2 σ π . \displaystyle =2 \frac{1}{2 \sqrt{\pi} \sigma}\left(-2 \sigma^2\right) \int_0^{+\infty} \mathrm{e}^{-\frac{x^2}{4^2}} \mathrm{~d}\left(-\frac{z^2}{4 \sigma^2}\right)=-\left.\frac{2 \sigma}{\sqrt{\pi}} \mathrm{e}^{-\frac{z^2}{\omega^2}}\right|_0 ^{+\infty}=\frac{2 \sigma}{\sqrt{\pi}} . = 2 2 π σ 1 ( − 2 σ 2 ) ∫ 0 + ∞ e − 4 2 x 2 d ( − 4 σ 2 z 2 ) = − π 2 σ e − ω 2 z 2 0 + ∞ = π 2 σ . 二、填空题: 11 ∼ 16 11 \sim 16 11 ∼ 16 (11) 当 x → 0 x \rightarrow 0 x → 0 f ( x ) = a x + b x 2 + ln ( 1 + x ) f(x)=a x+b x^{2}+\ln (1+x) f ( x ) = a x + b x 2 + ln ( 1 + x ) g ( x ) = e x 2 − cos x g(x)=\mathrm{e}^{x^{2}}-\cos x g ( x ) = e x 2 − cos x a b = a b= ab =
整体思想:lim x → 0 f ( x ) g ( x ) = 1 ⇒ a ⋅ b \displaystyle \lim _{x \rightarrow 0} \frac{f(x)}{g(x)}=1 \Rightarrow a \cdot b x → 0 lim g ( x ) f ( x ) = 1 ⇒ a ⋅ b 由f ( x ) = a x + b x 2 f(x)=a x+b x^{2} f ( x ) = a x + b x 2 f ( x ) = a x + b x 2 + x − 1 2 x 2 + o ( x 2 ) = ( a + 1 ) x + ( b − 1 2 ) x 2 + o ( x 2 ) . \displaystyle f(x)=a x+b x^2+x-\frac{1}{2} x^2+o\left(x^2\right)=(a+1) x+\left(b-\frac{1}{2}\right) x^2+o\left(x^2\right) . f ( x ) = a x + b x 2 + x − 2 1 x 2 + o ( x 2 ) = ( a + 1 ) x + ( b − 2 1 ) x 2 + o ( x 2 ) . g ( x ) = 1 + x 2 + o ( x 2 ) − [ 1 − 1 2 x 2 + o ( x 2 ) ] = 3 2 x 2 + o ( x 2 ) \displaystyle g(x)=1+x^2+o\left(x^2\right)-\left[1-\frac{1}{2} x^2+o\left(x^2\right)\right]=\frac{3}{2} x^2+o\left(x^2\right) g ( x ) = 1 + x 2 + o ( x 2 ) − [ 1 − 2 1 x 2 + o ( x 2 ) ] = 2 3 x 2 + o ( x 2 ) 1 = lim x → 0 f ( x ) g ( x ) = lim x → 0 ( a + 1 ) x + ( b − 1 2 ) x 2 + o ( x 2 ) 3 2 x 2 + o ( x 2 ) \displaystyle 1=\lim _{x \rightarrow 0} \frac{f(x)}{g(x)}=\lim _{x \rightarrow 0} \frac{(a+1) x+\left(b-\frac{1}{2}\right) x^2+o\left(x^2\right)}{\frac{3}{2} x^2+o\left(x^2\right)} 1 = x → 0 lim g ( x ) f ( x ) = x → 0 lim 2 3 x 2 + o ( x 2 ) ( a + 1 ) x + ( b − 2 1 ) x 2 + o ( x 2 ) ⇒ a + 1 = 0 , b − 1 2 = 3 2 ⇒ a = − 1 , b = 2. \displaystyle \Rightarrow a+1=0, \quad b-\frac{1}{2}=\frac{3}{2} \Rightarrow a=-1, b=2 . ⇒ a + 1 = 0 , b − 2 1 = 2 3 ⇒ a = − 1 , b = 2. (12) 曲面 z = x + 2 y + ln ( 1 + x 2 + y 2 ) z=x+2 y+\ln \left(1+x^{2}+y^{2}\right) z = x + 2 y + ln ( 1 + x 2 + y 2 ) ( 0 , 0 , 0 ) (0,0,0) ( 0 , 0 , 0 )
答 应填 x + 2 y − z = 0 x+2 y-z=0 x + 2 y − z = 0 切平面方程的公式:∂ F ∂ x ∣ ( x 0 , y 0 , z 0 ) ⋅ ( x − x 0 ) + ∂ F ∂ y ∣ ( x 0 , y 0 , z 0 ) ⋅ ( y − y 0 ) + ∂ F ∂ z ∣ ( x 0 , y 0 , z 0 ) ⋅ ( z − z 0 ) = 0 \left.\frac{\partial F}{\partial x}\right|_{\left(x_0, y_0, z_0\right)} \cdot\left(x-x_0\right)+\left.\frac{\partial F}{\partial y}\right|_{\left(x_0, y_0, z_0\right)} \cdot\left(y-y_0\right)+\left.\frac{\partial F}{\partial z}\right|_{\left(x_0, y_0, z_0\right)} \cdot\left(z-z_0\right)=0 ∂ x ∂ F ( x 0 , y 0 , z 0 ) ⋅ ( x − x 0 ) + ∂ y ∂ F ( x 0 , y 0 , z 0 ) ⋅ ( y − y 0 ) + ∂ z ∂ F ( x 0 , y 0 , z 0 ) ⋅ ( z − z 0 ) = 0 若曲面的方程为 F ( x , y , z ) = 0 F(x, y, z)=0 F ( x , y , z ) = 0 则该曲面在点 P ( x 0 , y 0 , z 0 ) P\left(x_0, y_0, z_0\right) P ( x 0 , y 0 , z 0 ) ( ∂ F ∂ x , ∂ F ∂ y , ∂ F ∂ z ) ∣ ( x 0 , y 0 , z 0 ) \left.\left(\frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z}\right)\right|_{\left(x_0, y_0, z_0\right)} ( ∂ x ∂ F , ∂ y ∂ F , ∂ z ∂ F ) ( x 0 , y 0 , z 0 ) 由于曲面在一点的切平面与曲面在该点的法向量垂直, 故曲面在点 P P P ( x − x 0 , y − y 0 , z − z 0 ) ⋅ ( ∂ F ∂ x , ∂ F ∂ y , ∂ F ∂ z ) ∣ ( x 0 , y 0 , z 0 ) = 0 \left.\left(x-x_0, y-y_0, z-z_0\right) \cdot\left(\frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z}\right)\right|_{\left(x_0, y_0, z_0\right)}=0 ( x − x 0 , y − y 0 , z − z 0 ) ⋅ ( ∂ x ∂ F , ∂ y ∂ F , ∂ z ∂ F ) ( x 0 , y 0 , z 0 ) = 0 令 F ( x , y , z ) = x + 2 y + ln ( 1 + x 2 + y 2 ) − z F(x, y, z)=x+2 y+\ln \left(1+x^2+y^2\right)-z F ( x , y , z ) = x + 2 y + ln ( 1 + x 2 + y 2 ) − z ( ∂ F ∂ x , ∂ F ∂ y , ∂ F ∂ z ) = ( 1 + 2 x 1 + x 2 + y 2 , 2 + 2 y 1 + x 2 + y 2 , − 1 ) \left(\frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z}\right)=\left(1+\frac{2 x}{1+x^2+y^2}, 2+\frac{2 y}{1+x^2+y^2},-1\right) ( ∂ x ∂ F , ∂ y ∂ F , ∂ z ∂ F ) = ( 1 + 1 + x 2 + y 2 2 x , 2 + 1 + x 2 + y 2 2 y , − 1 ) ( 0 , 0 , 0 ) (0,0,0) ( 0 , 0 , 0 ) ( 1 , 2 , − 1 ) (1,2,-1) ( 1 , 2 , − 1 ) 1 ⋅ ( x − 0 ) + 2 ( y − 0 ) + ( − 1 ) ( z − 0 ) = 0 1 \cdot(x-0)+2(y-0)+(-1)(z-0)=0 1 ⋅ ( x − 0 ) + 2 ( y − 0 ) + ( − 1 ) ( z − 0 ) = 0 切平面方程: x + 2 y − z = 0 x+2 y-z=0 x + 2 y − z = 0 (13) 设 f ( x ) f(x) f ( x ) f ( x ) = 1 − x , x ∈ [ 0 , 1 ] f(x)=1-x, x \in[0,1] f ( x ) = 1 − x , x ∈ [ 0 , 1 ] f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n π x \displaystyle f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos n \pi x f ( x ) = 2 a 0 + n = 1 ∑ ∞ a n cos nπ x ∑ n = 1 ∞ a 2 n = \displaystyle \sum_{n=1}^{\infty} a_{2 n}= n = 1 ∑ ∞ a 2 n =
答 应填 0 . 正弦级数与余弦级数 :设 f ( x ) f(x) f ( x ) 周期为 2 l 2 l 2 l . 记 C = { x ∣ f ( x ) = 1 2 [ f ( x − ) + f ( x + ) ] } C=\left\{x \left\lvert\, f(x)=\frac{1}{2}\left[f\left(x^{-}\right)+f\left(x^{+}\right)\right]\right.\right\} C = { x f ( x ) = 2 1 [ f ( x − ) + f ( x + ) ] } 当 f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) 只含正弦项 的正弦级数 f ( x ) = ∑ n = 1 ∞ b n sin n π x l ( x ∈ C ) \displaystyle f(x)=\sum_{n=1}^{\infty} b_n \sin \frac{n \pi x}{l} \quad(x \in C) f ( x ) = n = 1 ∑ ∞ b n sin l nπ x ( x ∈ C ) 其中 b n = 2 l ∫ 0 l f ( x ) sin n π x l d x ( n = 1 , 2 , ⋯ ) \displaystyle b_n=\frac{2}{l} \int_0^l f(x) \sin \frac{n \pi x}{l} \mathrm{~d} x \quad(n=1,2, \cdots) b n = l 2 ∫ 0 l f ( x ) sin l nπ x d x ( n = 1 , 2 , ⋯ ) 当 f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n π x l ( x ∈ C ) , \displaystyle f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty} a_n \cos \frac{n \pi x}{l} \quad(x \in C), f ( x ) = 2 a 0 + n = 1 ∑ ∞ a n cos l nπ x ( x ∈ C ) , 其中 a n = 2 l ∫ 0 l f ( x ) cos n π x l d x ( n = 0 , 1 , 2 , ⋯ ) \displaystyle a_n=\frac{2}{l} \int_0^l f(x) \cos \frac{n \pi x}{l} \mathrm{~d} x \quad(n=0,1,2, \cdots) a n = l 2 ∫ 0 l f ( x ) cos l nπ x d x ( n = 0 , 1 , 2 , ⋯ ) \displaystyle n ⩾ 1 n \geqslant 1 n ⩾ 1 a n = 2 ∫ 0 1 ( 1 − x ) cos n π x d x = 分布 2 [ ∫ 0 1 cos n π x d x − ∫ 0 1 x cos n π x d x ] \displaystyle a_n =2 \int_0^1(1-x) \cos n \pi x d x\xlongequal[]{\text{分布}}2\left[\int_0^1 \cos n \pi x d x-\int_0^1 x \cos n \pi x d x\right] a n = 2 ∫ 0 1 ( 1 − x ) cos nπ x d x 分布 2 [ ∫ 0 1 cos nπ x d x − ∫ 0 1 x cos nπ x d x ] = 2 [ 1 n π sin n π x ∣ 0 1 ⏟ 0 − 0 = 0 − 1 n π ∫ 0 1 x d ( sin n π x ) ⏟ 凑微分 ] \displaystyle =2\left[\underbrace{\left.\frac{1}{n \pi} \sin n \pi x\right|_0 ^1}_{0-0=0}-\underbrace{\frac{1}{n \pi} \int_0^1 x d(\sin n \pi x)}_{\text{凑微分}}\right] = 2 0 − 0 = 0 nπ 1 sin nπ x 0 1 − 凑微分 nπ 1 ∫ 0 1 x d ( sin nπ x ) = − 2 n π ∫ 0 1 x d ( sin n π x ) = 分布 − 2 n π ( x sin n π x ∣ 0 1 ⏟ 0 − 0 = 0 − ∫ 0 1 sin n π x d x ) \displaystyle =-\frac{2}{n \pi} \int_0^1 x d(\sin n \pi x)\xlongequal[]{\text{分布}}-\frac{2}{n \pi}\left(\underbrace{\left.x \sin n \pi x\right|_0 ^1}_{0-0=0}-\int_0^1 \sin n \pi x d x\right) = − nπ 2 ∫ 0 1 x d ( sin nπ x ) 分布 − nπ 2 0 − 0 = 0 x sin nπ x ∣ 0 1 − ∫ 0 1 sin nπ x d x = 2 n π ∫ 0 1 sin n π x d x = 凑微分 2 n π ⋅ ( − cos n π x n π ) ∣ 0 1 \displaystyle =\frac{2}{n \pi} \int_0^1 \sin n \pi x d x\xlongequal[]{\text{凑微分}}\left.\frac{2}{n \pi} \cdot\left(-\frac{\cos n \pi x}{n \pi}\right)\right|_0 ^1 = nπ 2 ∫ 0 1 sin nπ x d x 凑微分 nπ 2 ⋅ ( − nπ cos nπ x ) 0 1 = − 2 n 2 π 2 ( cos n π − 1 ) . \displaystyle =-\frac{2}{n^2 \pi^2}(\cos n \pi-1) . = − n 2 π 2 2 ( cos nπ − 1 ) . → 将 n 换成 2 n a 2 n = − 2 ( 2 n ) 2 π 2 ( cos 2 n π − 1 ) = 0 → cos 2 n π = 1 ∑ n = 1 ∞ a 2 n = 0 \displaystyle \xrightarrow[]{\text{将}n\text{换成}2n} a_{2 n} =-\frac{2}{(2 n)^2 \pi^2}(\cos 2 n \pi-1)=0 \xrightarrow[]{\cos 2 n \pi=1}\sum_{n=1}^{\infty} a_{2 n}=0 将 n 换成 2 n a 2 n = − ( 2 n ) 2 π 2 2 ( cos 2 nπ − 1 ) = 0 c o s 2 nπ = 1 n = 1 ∑ ∞ a 2 n = 0 类似题目 将函数 f ( x ) = 2 + ∣ x ∣ ( − 1 ≤ x ≤ 1 ) f(x)=2+|x|(-1 \leq x \leq 1) f ( x ) = 2 + ∣ x ∣ ( − 1 ≤ x ≤ 1 ) ∑ n = 1 ∞ 1 n 2 \displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2} n = 1 ∑ ∞ n 2 1 设函数 f ( x ) = π x + x 2 ( − π < x < π ) f(x)=\pi x+x^2(-\pi<x<\pi) f ( x ) = π x + x 2 ( − π < x < π ) a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) \displaystyle \frac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_n \cos n x+b_n \sin n x\right) 2 a 0 + n = 1 ∑ ∞ ( a n cos n x + b n sin n x ) b 3 b_3 b 3 \qquad 将函数 f ( x ) = x − 1 ( 0 ≤ x ≤ 2 ) f(x)=x-1(0 \leq x \leq 2) f ( x ) = x − 1 ( 0 ≤ x ≤ 2 ) 设 x 2 = ∑ n = 0 ∞ a n cos n x ( − π ≤ x ≤ π ) \displaystyle x^2=\sum_{n=0}^{\infty} a_n \cos n x(-\pi \leq x \leq \pi) x 2 = n = 0 ∑ ∞ a n cos n x ( − π ≤ x ≤ π ) a 2 = a_2= a 2 = \qquad 将函数 f ( x ) = 1 − x 2 ( 0 ≤ x ≤ π ) f(x)=1-x^2(0 \leq x \leq \pi) f ( x ) = 1 − x 2 ( 0 ≤ x ≤ π ) ∑ n = 1 ∞ ( − 1 ) n − 1 n 2 \displaystyle \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^2} n = 1 ∑ ∞ n 2 ( − 1 ) n − 1 (14) 设连续函数 f ( x ) f(x) f ( x ) f ( x + 2 ) − f ( x ) = x , ∫ 0 2 f ( x ) d x = 0 \displaystyle f(x+2)-f(x)=x, \int_{0}^{2} f(x) \mathrm{d} x=0 f ( x + 2 ) − f ( x ) = x , ∫ 0 2 f ( x ) d x = 0 ∫ 1 3 f ( x ) d x = \displaystyle \int_{1}^{3} f(x) \mathrm{d} x= ∫ 1 3 f ( x ) d x =
答 应填 1 2 \frac{1}{2} 2 1 ∫ 1 3 f ( x ) d x = ∫ 0 3 f ( x ) d x − ∫ 0 1 f ( x ) d x \displaystyle \int_1^3 f(x) d x =\int_0^3 f(x) d x-\int_0^1 f(x) d x ∫ 1 3 f ( x ) d x = ∫ 0 3 f ( x ) d x − ∫ 0 1 f ( x ) d x = ∫ 0 3 → ∫ 0 2 + ∫ 2 3 ∫ 0 2 f ( x ) d x + ∫ 2 3 f ( x ) d x − ∫ 0 1 f ( x ) d x \displaystyle \xlongequal[]{\int_0^3 \rightarrow \int_0^2+\int_2^3}\int_0^2 f(x) d x+\int_2^3 f(x) d x-\int_0^1 f(x) d x ∫ 0 3 → ∫ 0 2 + ∫ 2 3 ∫ 0 2 f ( x ) d x + ∫ 2 3 f ( x ) d x − ∫ 0 1 f ( x ) d x = ∫ 0 2 f ( x ) d x = 0 ∫ 2 3 f ( x ) d x − ∫ 0 1 f ( x ) d x \displaystyle \xlongequal[]{\int_{0}^{2} f(x) \mathrm{d} x=0}\int_2^3 f(x) d x-\int_0^1 f(x) d x ∫ 0 2 f ( x ) d x = 0 ∫ 2 3 f ( x ) d x − ∫ 0 1 f ( x ) d x = ∫ 0 1 f ( x + 2 ) d x = t = x + 2 ∫ 2 3 f ( x ) d x ∫ 0 1 f ( x + 2 ) d x − ∫ 0 1 f ( x ) d x = f ( x + 2 ) − f ( x ) = x ∫ 0 1 x d x = 牛莱 1 2 x 2 ∣ 0 1 = 1 2 . \displaystyle \xlongequal[]{\int_0^1 f(x+2) d x\xlongequal[]{t=x+2}\int_2^3 f(x) d x }\int_0^1 f(x+2) d x-\int_0^1 f(x) d x\xlongequal[]{f(x+2)-f(x)=x}\int_0^1 x d x \xlongequal[]{\text{牛莱}}\left.\frac{1}{2} x^2\right|_0 ^1=\frac{1}{2} . ∫ 0 1 f ( x + 2 ) d x t = x + 2 ∫ 2 3 f ( x ) d x ∫ 0 1 f ( x + 2 ) d x − ∫ 0 1 f ( x ) d x f ( x + 2 ) − f ( x ) = x ∫ 0 1 x d x 牛莱 2 1 x 2 0 1 = 2 1 . (15) 已知向量 α 1 = ( 1 0 1 1 ) , α 2 = ( − 1 − 1 0 1 ) , α 3 = ( 0 1 − 1 1 ) , β = ( 1 1 1 − 1 ) , γ = k 1 α 1 + k 2 α 2 + k 3 α 3 \displaystyle \boldsymbol{\alpha}_{1}=\left(\begin{array}{l}1 \\ 0 \\ 1 \\ 1\end{array}\right), \boldsymbol{\alpha}_{2}=\left(\begin{array}{c}-1 \\ -1 \\ 0 \\ 1\end{array}\right), \boldsymbol{\alpha}_{3}=\left(\begin{array}{c}0 \\ 1 \\ -1 \\ 1\end{array}\right), \boldsymbol{\beta}=\left(\begin{array}{c}1 \\ 1 \\ 1 \\ -1\end{array}\right), \boldsymbol{\gamma}=k_{1} \boldsymbol{\alpha}_{1}+k_{2} \boldsymbol{\alpha}_{2}+k_{3} \boldsymbol{\alpha}_{3} α 1 = 1 0 1 1 , α 2 = − 1 − 1 0 1 , α 3 = 0 1 − 1 1 , β = 1 1 1 − 1 , γ = k 1 α 1 + k 2 α 2 + k 3 α 3 γ T α i = β T α i ( i = 1 , 2 , 3 ) \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_{i}=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}_{i}(i=1,2,3) γ T α i = β T α i ( i = 1 , 2 , 3 ) k 1 2 + k 2 2 + k 3 2 = k_{1}^{2}+k_{2}^{2}+k_{3}^{2}= k 1 2 + k 2 2 + k 3 2 =
答 应填 11 9 \frac{11}{9} 9 11 向量内积的概念 设有 n n n x = ( x 1 x 2 ⋮ x n ) , y = ( y 1 y 2 ⋮ y n ) , \displaystyle \boldsymbol{x}=\left(\begin{array}{c}x_1 \\x_2 \\\vdots \\x_n\end{array}\right), \quad \boldsymbol{y}=\left(\begin{array}{c}y_1 \\y_2 \\\vdots \\y_n\end{array}\right) \text {, } x = x 1 x 2 ⋮ x n , y = y 1 y 2 ⋮ y n , 令( x , y ) = x 1 y 1 + x 2 y 2 + ⋯ + x n y n , (\boldsymbol{x}, \boldsymbol{y})=x_1 y_1+x_2 y_2+\cdots+x_n y_n, ( x , y ) = x 1 y 1 + x 2 y 2 + ⋯ + x n y n , ( x , y ) (\boldsymbol{x}, \boldsymbol{y}) ( x , y ) x \boldsymbol{x} x y \boldsymbol{y} y ( x , y ) = x T y = y T x , (\boldsymbol{x}, \boldsymbol{y})=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{x}, ( x , y ) = x T y = y T x , 当 ( x , y ) = 0 (\boldsymbol{x}, \boldsymbol{y})=0 ( x , y ) = 0 x \boldsymbol{x} x y \boldsymbol{y} y ( x , x ) = ∥ x ∥ 2 (\boldsymbol{x}, \boldsymbol{x})=\|\boldsymbol{x}\|^2 ( x , x ) = ∥ x ∥ 2 x \boldsymbol{x} x 解:注意到 α 1 T α 2 = α 2 T α 3 = α 3 T α 1 = 0 \boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{\alpha}_2=\boldsymbol{\alpha}_2^{\mathrm{T}} \boldsymbol{\alpha}_3=\boldsymbol{\alpha}_3^{\mathrm{T}} \boldsymbol{\alpha}_1=0 α 1 T α 2 = α 2 T α 3 = α 3 T α 1 = 0 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 由γ T α i = β T α i ( i = 1 , 2 , 3 ) \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_{i}=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}_{i}(i=1,2,3) γ T α i = β T α i ( i = 1 , 2 , 3 ) 计算γ T α i \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_{i} γ T α i γ T α 1 = ( k 1 α 1 + k 2 α 2 + k 3 α 3 ) T α 1 = k 1 α 1 ⊤ α 1 + k 2 α 2 ⊤ α 1 + k 3 α 3 ⊤ α 1 ⏟ α 1 T α 2 = α 2 T α 3 = α 3 T α 1 = 0 = k 1 ∥ α 1 ∥ 2 \displaystyle \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_1=\left(k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+k_3 \boldsymbol{\alpha}_3\right)^{\mathrm{T}} \boldsymbol{\alpha}_1=k_1 \alpha_1^{\top} \alpha_1\underbrace{+k_2 \alpha_2^{\top} \alpha_1+k_3 \alpha_3^{\top} \alpha_1}_{\boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{\alpha}_2=\boldsymbol{\alpha}_2^{\mathrm{T}} \boldsymbol{\alpha}_3=\boldsymbol{\alpha}_3^{\mathrm{T}} \boldsymbol{\alpha}_1=0}=k_1\left\|\boldsymbol{\alpha}_1\right\|^2 γ T α 1 = ( k 1 α 1 + k 2 α 2 + k 3 α 3 ) T α 1 = k 1 α 1 ⊤ α 1 α 1 T α 2 = α 2 T α 3 = α 3 T α 1 = 0 + k 2 α 2 ⊤ α 1 + k 3 α 3 ⊤ α 1 = k 1 ∥ α 1 ∥ 2 γ T α 2 = ( k 1 α 1 + k 2 α 2 + k 3 α 3 ) T α 2 = k 2 ∥ α 2 ∥ 2 \displaystyle \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_2=\left(k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+k_3 \boldsymbol{\alpha}_3\right)^{\mathrm{T}} \boldsymbol{\alpha}_2=k_2\left\|\boldsymbol{\alpha}_2\right\|^2 γ T α 2 = ( k 1 α 1 + k 2 α 2 + k 3 α 3 ) T α 2 = k 2 ∥ α 2 ∥ 2 γ T α 3 = ( k 1 α 1 + k 2 α 2 + k 3 α 3 ) T α 3 = k 3 ∥ α 3 ∥ 2 \displaystyle \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_3=\left(k_1 \boldsymbol{\alpha}_1+k_2 \boldsymbol{\alpha}_2+k_3 \boldsymbol{\alpha}_3\right)^{\mathrm{T}} \boldsymbol{\alpha}_3=k_3\left\|\boldsymbol{\alpha}_3\right\|^2 γ T α 3 = ( k 1 α 1 + k 2 α 2 + k 3 α 3 ) T α 3 = k 3 ∥ α 3 ∥ 2 计算β T α \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha} β T α β T α 1 = 1 , β T α 2 = − 3 , β T α 3 = − 1 \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}_1=1, \quad \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}_2=-3, \quad \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}_3=-1 β T α 1 = 1 , β T α 2 = − 3 , β T α 3 = − 1 由γ T α i = β T α i ( i = 1 , 2 , 3 ) \boldsymbol{\gamma}^{\mathrm{T}} \boldsymbol{\alpha}_{i}=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}_{i}(i=1,2,3) γ T α i = β T α i ( i = 1 , 2 , 3 ) k 1 ∥ α 1 ∥ 2 = 1 , k 2 ∥ α 2 ∥ 2 = − 3 , k 3 ∥ α 3 ∥ 2 = − 1 k_1\left\|\alpha_1\right\|^2=1\text{,} \quad k_2\left\|\alpha_2\right\|^2=-3\text{,} \quad k_3\left\|\alpha_3\right\|^2=-1 k 1 ∥ α 1 ∥ 2 = 1 , k 2 ∥ α 2 ∥ 2 = − 3 , k 3 ∥ α 3 ∥ 2 = − 1 即3 k 1 = 1 , 3 k 2 = − 3 , 3 k 3 = − 1. 3 k_1=1, \quad 3 k_2=-3, \quad 3 k_3=-1 . 3 k 1 = 1 , 3 k 2 = − 3 , 3 k 3 = − 1. k 1 = 1 3 , k 2 = − 1 , k 3 = − 1 3 k_1=\frac{1}{3}, k_2=-1, k_3=-\frac{1}{3} k 1 = 3 1 , k 2 = − 1 , k 3 = − 3 1 因此, k 1 2 + k 2 2 + k 3 2 = 1 9 + 1 + 1 9 = 11 9 k_1^2+k_2^2+k_3^2=\frac{1}{9}+1+\frac{1}{9}=\frac{11}{9} k 1 2 + k 2 2 + k 3 2 = 9 1 + 1 + 9 1 = 9 11 (16) 设随机变量 X X X Y Y Y X ∼ B ( 1 , 1 3 ) , Y ∼ B ( 2 , 1 2 ) X \sim B\left(1, \frac{1}{3}\right), Y \sim B\left(2, \frac{1}{2}\right) X ∼ B ( 1 , 3 1 ) , Y ∼ B ( 2 , 2 1 ) P { X = Y } = P\{X=Y\}= P { X = Y } =
答 应填 1 3 \frac{1}{3} 3 1 C n k = n ! k ! ( n − k ) ! C_n^k=\frac{n!}{k!(n-k)!} C n k = k ! ( n − k )! n ! C 5 3 = 5 ! 3 ! ⋅ 2 ! = 5 × 4 × 3 × 2 × 1 ( 3 × 2 × 1 ) ⋅ ( 2 × 1 ) = 10 C_5^3=\frac{5!}{3!\cdot 2!}=\frac{5 \times 4 \times 3 \times 2 \times 1}{(3 \times 2 \times 1) \cdot(2 \times 1)}=10 C 5 3 = 3 ! ⋅ 2 ! 5 ! = ( 3 × 2 × 1 ) ⋅ ( 2 × 1 ) 5 × 4 × 3 × 2 × 1 = 10 x 0 1 p 2 3 1 3 \displaystyle \begin{array}{l|l|l}x & 0 & 1 \\\hline p & \frac{2}{3} & \frac{1}{3}\end{array} x p 0 3 2 1 3 1 Y 0 1 2 p 1 4 1 2 1 4 \displaystyle \begin{array}{c|c|c|c}Y & 0 & 1 & 2 \\\hline p & \frac{1}{4} & \frac{1}{2} & \frac{1}{4}\end{array} Y p 0 4 1 1 2 1 2 4 1 P { X = Y } = 分析 X = Y P { X = 0 , Y = 0 } + P { X = 1 , Y = 1 } \displaystyle P\{X=Y\} \xlongequal[]{\text{分析}X=Y}P\{X=0, Y=0\}+P\{X=1, Y=1\} P { X = Y } 分析 X = Y P { X = 0 , Y = 0 } + P { X = 1 , Y = 1 } = 独立性 P { X = 0 } P { Y = 0 } + P { X = 1 } P { Y = 1 } \displaystyle \xlongequal[]{\text{独立性}}P\{X=0\} P\{Y=0\}+P\{X=1\} P\{Y=1\} 独立性 P { X = 0 } P { Y = 0 } + P { X = 1 } P { Y = 1 } X ∼ B ( 1 , 1 3 ) P { X = 0 } = C 1 0 ( 1 3 ) 0 ( 2 3 ) 1 = 2 3 P { X = 1 } = C 1 1 ( 1 3 ) 1 ( 2 3 ) 0 = 1 3 Y ∼ B ( 2 , 1 2 ) P { Y = 0 } = C 2 0 ( 1 2 ) 0 ( 1 2 ) 2 = 1 4 P { Y = 1 } = C 2 1 ( 1 2 ) 1 ( 1 2 ) 1 = 1 2 \displaystyle \begin{array}{lll}X \sim B\left(1, \frac{1}{3}\right) P\{X=0\}=C_1^0\left(\frac{1}{3}\right)^0\left(\frac{2}{3}\right)^1=\frac{2}{3} P\{X=1\}=C_1^1\left(\frac{1}{3}\right)^1\left(\frac{2}{3}\right)^0=\frac{1}{3} \\ Y \sim B\left(2, \frac{1}{2}\right) P\{Y=0\}=C_2^0\left(\frac{1}{2}\right)^0\left(\frac{1}{2}\right)^2=\frac{1}{4} P\{Y=1\}=C_2^1\left(\frac{1}{2}\right)^1\left(\frac{1}{2}\right)^1=\frac{1}{2}\end{array} X ∼ B ( 1 , 3 1 ) P { X = 0 } = C 1 0 ( 3 1 ) 0 ( 3 2 ) 1 = 3 2 P { X = 1 } = C 1 1 ( 3 1 ) 1 ( 3 2 ) 0 = 3 1 Y ∼ B ( 2 , 2 1 ) P { Y = 0 } = C 2 0 ( 2 1 ) 0 ( 2 1 ) 2 = 4 1 P { Y = 1 } = C 2 1 ( 2 1 ) 1 ( 2 1 ) 1 = 2 1 = 2 3 × 1 4 + 1 3 × 1 2 = 1 6 + 1 6 = 1 3 . \displaystyle = \frac{2}{3} \times \frac{1}{4}+\frac{1}{3} \times \frac{1}{2} =\frac{1}{6}+\frac{1}{6}=\frac{1}{3} . = 3 2 × 4 1 + 3 1 × 2 1 = 6 1 + 6 1 = 3 1 . 三、解答题: 17 ∼ 22 17 \sim 22 17 ∼ 22 (17) (本题满分 10 分)y = y ( x ) ( x > 0 ) y=y(x)(x>0) y = y ( x ) ( x > 0 ) ( 1 , 2 ) (1,2) ( 1 , 2 ) P ( x , y ) P(x, y) P ( x , y ) y y y y y y y ( x ) y(x) y ( x ) f ( x ) = ∫ 1 x y ( t ) d t \displaystyle f(x)=\int_{1}^{x} y(t) \mathrm{d} t f ( x ) = ∫ 1 x y ( t ) d t ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ )
P ( x , y ) \displaystyle P(x, y) P ( x , y ) y − y 0 = y ′ ( x 0 ) ( x − x 0 ) y-y_0=y^{\prime}\left(x_0\right)\left(x-x_0\right) y − y 0 = y ′ ( x 0 ) ( x − x 0 ) 该曲线上任一点 P ( x , y ) P(x, y) P ( x , y ) y y y y y y 求截距:\displaystyle x = 0 x=0 x = 0 ∣ O A ∣ = y = y 0 − y ′ ( x 0 ) x 0 |O A|=y=y_0-y^{\prime}\left(x_0\right) x_0 ∣ O A ∣ = y = y 0 − y ′ ( x 0 ) x 0 该点处的切线在 y y y ∣ P H ∣ = x 0 \displaystyle |P H|=x_0 ∣ P H ∣ = x 0 ∣ O A ∣ = ∣ P H ∣ \displaystyle |O A|=|P H| ∣ O A ∣ = ∣ P H ∣ x 0 = y 0 − y ′ ( x 0 ) x 0 x_0=y_0-y^{\prime}\left(x_0\right) x_0 x 0 = y 0 − y ′ ( x 0 ) x 0 → 整理 y − x y ′ = x → 同除 x y ′ − 1 x y = − 1 \displaystyle \xrightarrow[]{\text{整理}}y-x y^{\prime}=x \xrightarrow{\text{ 同除 } x} y^{\prime}-\frac{1}{x} y=-1 整理 y − x y ′ = x 同除 x y ′ − x 1 y = − 1 → p = − 1 x , q = − 1 y = e ∫ 1 x d x [ ∫ ( − 1 ) e − ∫ 1 x d x d x + C ] \displaystyle \xrightarrow[]{ p=-\frac{1}{x}, q=- 1}y=e^{\int \frac{1}{x} d x}\left[\int(-1) e^{-\int \frac{1}{x} d x} d x+C\right] p = − x 1 , q = − 1 y = e ∫ x 1 d x [ ∫ ( − 1 ) e − ∫ x 1 d x d x + C ] = e ln x [ ∫ ( − 1 ) e − ln x d x + C ] \displaystyle =e^{\ln x}\left[\int(-1) e^{-\ln x} d x+C\right] = e l n x [ ∫ ( − 1 ) e − l n x d x + C ] = x [ ∫ ( − 1 ) 1 x d x + C ] \displaystyle =x\left[\int(-1) \frac{1}{x} d x+C\right] = x [ ∫ ( − 1 ) x 1 d x + C ] = x [ − ln x + C ] \displaystyle =x[-\ln x+C] = x [ − ln x + C ] y ( 1 ) = 2 \displaystyle y(1)=2 y ( 1 ) = 2 2 = 1 ⋅ [ − ln 1 + C ] ,得 C = 2 2=1 \cdot[-\ln 1+C] \text { ,得 } C=2 2 = 1 ⋅ [ − ln 1 + C ] ,得 C = 2 从而y的方程:y = x ( 2 − ln x ) \displaystyle y=x(2-\ln x) y = x ( 2 − ln x ) (2) 求函数 f ( x ) = ∫ 1 x y ( t ) d t \displaystyle f(x)=\int_{1}^{x} y(t) \mathrm{d} t f ( x ) = ∫ 1 x y ( t ) d t ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ ) f ( x ) = ∫ 1 x y ( t ) d t = ∫ 1 x t ⋅ ( 2 − ln t ) d t \displaystyle f(x)=\int_1^x y(t) d t=\int_1^x t \cdot(2-\ln t) d t f ( x ) = ∫ 1 x y ( t ) d t = ∫ 1 x t ⋅ ( 2 − ln t ) d t 一阶导求极值:f ′ ( x ) = x ⋅ ( 2 − ln x ) = 0 \displaystyle f^{\prime}(x)=x \cdot(2-\ln x)=0 f ′ ( x ) = x ⋅ ( 2 − ln x ) = 0 x = 0 或 x = e 2 x=0 \text { 或 } x=e^2 x = 0 或 x = e 2 \displaystyle x > 0 x>0 x > 0 x = e 2 x=e^2 x = e 2 通过增减性判断是否是最值 \displaystyle 0 < x < e 2 , f ′ ( x ) > 0 , 0<x<e^2, f^{\prime}(x)>0, 0 < x < e 2 , f ′ ( x ) > 0 , \displaystyle x > e 2 , f ′ ( x ) < 0 , x>e^2, f^{\prime}(x)<0, x > e 2 , f ′ ( x ) < 0 , 则 x = e 2 \displaystyle x = e^2 x = e 2 f ( x ) \displaystyle f(x) f ( x ) ( 0 , + ∞ ) \displaystyle (0, +\infty) ( 0 , + ∞ ) → x = e 2 f m a x = f ( e 2 ) = ∫ 1 e 2 t ( 2 − ln t ) d t \displaystyle \xrightarrow[]{x = e^2 }f_{max}=f\left(e^2\right) =\int_1^{e^2} t(2-\ln t) d t x = e 2 f ma x = f ( e 2 ) = ∫ 1 e 2 t ( 2 − ln t ) d t = 拆开 ∫ 1 e 2 2 t d t − ∫ 1 e 2 t ln t d t \displaystyle \xlongequal[]{\text{拆开}}\int_1^{e^2} 2 t d t-\int_1^{e^2} t \ln t d t 拆开 ∫ 1 e 2 2 t d t − ∫ 1 e 2 t ln t d t = 凑微分 + 分布 t 2 ∣ 1 e 2 − 1 2 ∫ 1 e 2 ln t d ( t 2 ) \displaystyle \xlongequal[]{\text{凑微分}+\text{分布}}\left.t^2\right|_1 ^{e^2}-\frac{1}{2} \int_1^{e^2} \ln t d\left(t^2\right) 凑微分 + 分布 t 2 1 e 2 − 2 1 ∫ 1 e 2 ln t d ( t 2 ) = 脆弱坚强 e 4 − 1 − 1 2 [ t 2 ⋅ ln t ∣ 1 e 2 − ∫ 1 e 2 t 2 ⋅ d ( ln t ) ] \displaystyle \xlongequal[]{\text{脆弱坚强}}e^4-1-\frac{1}{2}\left[\left.t^2 \cdot \ln t\right|_1 ^{e^2}-\int_1^{e^2} t^2 \cdot d(\ln t)\right] 脆弱坚强 e 4 − 1 − 2 1 [ t 2 ⋅ ln t 1 e 2 − ∫ 1 e 2 t 2 ⋅ d ( ln t ) ] = ( ln t ) ′ = 1 t e 4 − 1 − 1 2 [ 2 e 4 − 0 − ∫ 1 e 2 t 2 ⋅ 1 t d t ] \displaystyle \xlongequal[]{(\ln t)^{\prime}=\frac{1}{t}}e^4-1-\frac{1}{2}\left[2 e^4-0-\int_1^{e^2} t^2 \cdot \frac{1}{t} d t\right] ( l n t ) ′ = t 1 e 4 − 1 − 2 1 [ 2 e 4 − 0 − ∫ 1 e 2 t 2 ⋅ t 1 d t ] = 牛莱 e 4 − e 4 − 1 + 1 2 ⋅ t 2 2 ∣ 1 e 2 \displaystyle \xlongequal[]{\text{牛莱}}e^4-e^4-1+\left.\frac{1}{2} \cdot \frac{t^2}{2}\right|_1 ^{e^2} 牛莱 e 4 − e 4 − 1 + 2 1 ⋅ 2 t 2 1 e 2 = − 1 + 1 2 ( e 4 2 − 1 2 ) = e 4 4 − 5 4 \displaystyle =-1+\frac{1}{2}\left(\frac{e^4}{2}-\frac{1}{2}\right)=\frac{e^4}{4}-\frac{5}{4} = − 1 + 2 1 ( 2 e 4 − 2 1 ) = 4 e 4 − 4 5 (18) (本题满分 12 分)f ( x , y ) = ( y − x 2 ) ( y − x 3 ) f(x, y)=\left(y-x^{2}\right)\left(y-x^{3}\right) f ( x , y ) = ( y − x 2 ) ( y − x 3 )
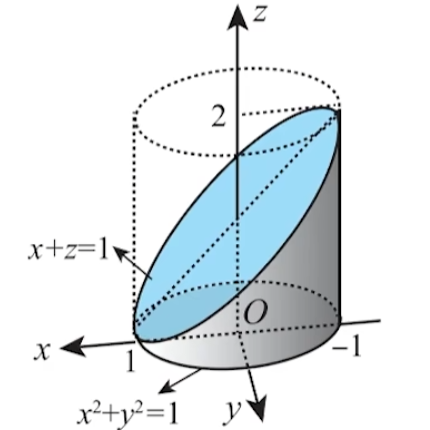
求条件极值的方法 (1) f x = f y = 0 \displaystyle \begin{aligned} f_x = f_y = 0 \end{aligned} f x = f y = 0 (2) A = f x x , B = f x y , C = f y y \displaystyle \begin{aligned} A = f_{xx}, B = f_{xy}, C = f_{yy} \end{aligned} A = f xx , B = f x y , C = f yy A C − B 2 { > 0 { A > 0 : 极小 A < 0 : 极大 < 0 : 非极值 = 0 : 进一步讨论 \displaystyle \begin{aligned} AC - B^2 \begin{cases} > 0 & \begin{cases} A > 0: \text{极小} \\ A < 0: \text{极大} \end{cases} \\ < 0: \text{非极值} \\ = 0: \text{进一步讨论} \end{cases} \end{aligned} A C − B 2 ⎩ ⎨ ⎧ > 0 < 0 : 非极值 = 0 : 进一步讨论 { A > 0 : 极小 A < 0 : 极大 f ( x , y ) = ( y − x 2 ) ( y − x 3 ) \displaystyle f(x, y) = (y - x^2)(y - x^3) f ( x , y ) = ( y − x 2 ) ( y − x 3 ) = 乘法分配 y 2 − x 3 y − x 2 y + x 5 \displaystyle \xlongequal[]{\text{乘法分配}} y^2 - x^3y - x^2y + x^5 乘法分配 y 2 − x 3 y − x 2 y + x 5 求可能的极值点,也就是驻点 f x ′ = − 3 x 2 y − 2 x y + 5 x 4 \displaystyle f'_x = -3x^2y - 2xy + 5x^4 f x ′ = − 3 x 2 y − 2 x y + 5 x 4 f y ′ = 2 y − x 3 − x 2 \displaystyle f'_y = 2y - x^3 - x^2 f y ′ = 2 y − x 3 − x 2 令 { f x ′ = 0 f y ′ = 0 \displaystyle \begin{cases} f'_x = 0 \\ f'_y = 0 \end{cases} { f x ′ = 0 f y ′ = 0 { − 3 x 2 y − 2 x y + 5 x 4 = 0 2 y − x 3 − x 2 = 0 \displaystyle \begin{cases} -3x^2y - 2xy + 5x^4 = 0 \\ 2y - x^3 - x^2 = 0 \end{cases} { − 3 x 2 y − 2 x y + 5 x 4 = 0 2 y − x 3 − x 2 = 0 y = x 3 + x 2 2 → 代入消元法 \displaystyle y = \frac{x^3 + x^2}{2} \xrightarrow[]{\text{代入消元法}} y = 2 x 3 + x 2 代入消元法 − 3 x 2 ⋅ x 3 + x 2 2 − 2 x ⋅ x 3 + x 2 2 + 5 x 4 = 0 \displaystyle -3x^2 \cdot \frac{x^3 + x^2}{2} - 2x \cdot \frac{x^3 + x^2}{2} + 5x^4 = 0 − 3 x 2 ⋅ 2 x 3 + x 2 − 2 x ⋅ 2 x 3 + x 2 + 5 x 4 = 0 → 整理 − 3 2 ⋅ ( x 5 + x 4 ) − ( x 4 + x 3 ) + 5 x 4 = 0 \displaystyle \xrightarrow[]{\text{整理}}-\frac{3}{2} \cdot (x^5 + x^4) - (x^4 + x^3) + 5x^4 = 0 整理 − 2 3 ⋅ ( x 5 + x 4 ) − ( x 4 + x 3 ) + 5 x 4 = 0 → 合并同类项 − 3 2 x 5 + ( − 3 2 − 1 + 5 ) x 4 − x 3 = 0 \displaystyle \xrightarrow[]{\text{合并同类项}}-\frac{3}{2}x^5 + \left(-\frac{3}{2} - 1 + 5\right)x^4 - x^3 = 0 合并同类项 − 2 3 x 5 + ( − 2 3 − 1 + 5 ) x 4 − x 3 = 0 → 整理 − 3 2 x 5 + 5 2 x 4 − x 3 = 0 \displaystyle \xrightarrow[]{\text{整理}}-\frac{3}{2}x^5 + \frac{5}{2}x^4 - x^3 = 0 整理 − 2 3 x 5 + 2 5 x 4 − x 3 = 0 → 同除 x 3 − 3 2 x 2 + 5 2 x − 1 = 0 \displaystyle \xrightarrow[]{\text{同除}x^3}-\frac{3}{2}x^2 + \frac{5}{2}x - 1 = 0 同除 x 3 − 2 3 x 2 + 2 5 x − 1 = 0 → 同乘 2 3 x 2 − 5 x + 2 = 0 \displaystyle \xrightarrow[]{\text{同乘}2}3x^2 - 5x + 2 = 0 同乘 2 3 x 2 − 5 x + 2 = 0 → 因式分解 1 − 1 3 2 ( x − 1 ) ( 3 x − 2 ) = 0 \displaystyle \xrightarrow[\text{因式分解}]{\begin{array}{lr}1 & -1 \\3 & 2\end{array}}(x - 1)(3x - 2) = 0 1 3 − 1 2 因式分解 ( x − 1 ) ( 3 x − 2 ) = 0 得 x = 0 , x = 1 , x = 2 3 \displaystyle x = 0, x = 1, x = \frac{2}{3} x = 0 , x = 1 , x = 3 2 ( x , y ) \displaystyle (x, y) ( x , y ) ( 0 , 0 ) , ( 1 , 1 ) , ( 2 3 , 10 27 ) \displaystyle \left(0, 0\right), \left(1, 1\right), \left(\frac{2}{3}, \frac{10}{27}\right) ( 0 , 0 ) , ( 1 , 1 ) , ( 3 2 , 27 10 ) 求A , B , C A,B,C A , B , C 由一阶导 f x ′ = − 3 x 2 y − 2 x y + 5 x 4 \displaystyle f'_x = -3x^2y - 2xy + 5x^4 f x ′ = − 3 x 2 y − 2 x y + 5 x 4 f y ′ = 2 y − x 3 − x 2 \displaystyle f'_y = 2y - x^3 - x^2 f y ′ = 2 y − x 3 − x 2 求二阶导 { A = f x x ′ ′ = 20 x 3 − 6 x y − 2 y B = f x y ′ ′ = − 3 x 2 − 2 x C = f y y ′ ′ = 2 \displaystyle \begin{cases} A = f''_{xx} = 20x^3 - 6xy - 2y \\ B = f''_{xy} = -3x^2 - 2x \\ C = f''_{yy} = 2 \end{cases} ⎩ ⎨ ⎧ A = f xx ′′ = 20 x 3 − 6 x y − 2 y B = f x y ′′ = − 3 x 2 − 2 x C = f yy ′′ = 2 分别讨论三种情况( x , y ) \displaystyle (x, y) ( x , y ) ( 0 , 0 ) , ( 1 , 1 ) , ( 2 3 , 10 27 ) \displaystyle \left(0, 0\right), \left(1, 1\right), \left(\frac{2}{3}, \frac{10}{27}\right) ( 0 , 0 ) , ( 1 , 1 ) , ( 3 2 , 27 10 ) 当 x = 0 , y = 0 \displaystyle x = 0, y = 0 x = 0 , y = 0 A , B , C A,B,C A , B , C A = 0 − 0 − 0 = 0 \displaystyle A = 0 - 0 - 0 = 0 A = 0 − 0 − 0 = 0 B = 0 − 0 = 0 \displaystyle B = 0 - 0 = 0 B = 0 − 0 = 0 C = 2 \displaystyle C = 2 C = 2 A C − B 2 = 0 ⋅ 2 − 0 = 0 \displaystyle AC - B^2 = 0 \cdot 2 - 0 = 0 A C − B 2 = 0 ⋅ 2 − 0 = 0 f ( x , y ) = ( y − x 2 ) ( y − x 3 ) \displaystyle f(x, y) = (y - x^2)(y - x^3) f ( x , y ) = ( y − x 2 ) ( y − x 3 ) 取 y = 2 x 2 \displaystyle y = 2x^2 y = 2 x 2 f ( x , y ) = ( 2 x 2 − x 2 ) ( x 2 − x 3 ) = x 2 ⋅ ( x 2 − x 3 ) = x 4 ⋅ ( 1 − x ) > 0 \displaystyle f(x, y) = (2x^2 - x^2)(x^2 - x^3) = x^2 \cdot (x^2 - x^3) = x^4 \cdot (1 - x) > 0 f ( x , y ) = ( 2 x 2 − x 2 ) ( x 2 − x 3 ) = x 2 ⋅ ( x 2 − x 3 ) = x 4 ⋅ ( 1 − x ) > 0 取 y = 2 x 3 \displaystyle y = 2x^3 y = 2 x 3 f ( x , y ) = ( 2 x 3 − x 2 ) ( 2 x 3 − x 3 ) = ( 2 x 3 − x 2 ) ⋅ x 3 = x 5 ( 2 x − 1 ) < 0 \displaystyle f(x, y) = (2x^3 - x^2)(2x^3 - x^3) = (2x^3 - x^2) \cdot x^3 = x^5(2x - 1) < 0 f ( x , y ) = ( 2 x 3 − x 2 ) ( 2 x 3 − x 3 ) = ( 2 x 3 − x 2 ) ⋅ x 3 = x 5 ( 2 x − 1 ) < 0 有的点大、有的点小、所以点 ( 0 , 0 ) \displaystyle (0,0) ( 0 , 0 ) ( x , y ) = ( 1 , 1 ) \displaystyle (x, y) = (1,1) ( x , y ) = ( 1 , 1 ) A , B , C A,B,C A , B , C A = 20 − 6 − 2 = 12 \displaystyle A = 20 - 6 - 2 = 12 A = 20 − 6 − 2 = 12 B = − 5 \displaystyle B = -5 B = − 5 C = 2 \displaystyle C = 2 C = 2 A C − B 2 = 24 − 25 = − 1 < 0 \displaystyle AC - B^2 = 24 - 25 = -1 < 0 A C − B 2 = 24 − 25 = − 1 < 0 ( x , y ) = ( 1 , 1 ) \displaystyle (x, y) = (1,1) ( x , y ) = ( 1 , 1 ) ( x , y ) = ( 2 3 , 10 27 ) \displaystyle (x, y) = \left(\frac{2}{3}, \frac{10}{27}\right) ( x , y ) = ( 3 2 , 27 10 ) 求A , B , C A,B,C A , B , C A = f x x ′ ′ = 20 x 3 − 6 x y − 2 y = 20 ( 2 3 ) 3 − 6 ⋅ 2 3 ⋅ 10 27 − 2 ⋅ 10 27 \displaystyle A = f''_{xx} = 20x^3 - 6xy - 2y = 20\left(\frac{2}{3}\right)^3 - 6\cdot\frac{2}{3}\cdot\frac{10}{27} - 2\cdot\frac{10}{27} A = f xx ′′ = 20 x 3 − 6 x y − 2 y = 20 ( 3 2 ) 3 − 6 ⋅ 3 2 ⋅ 27 10 − 2 ⋅ 27 10 = 20 ⋅ 8 27 − 4 ⋅ 10 27 − 2 ⋅ 10 27 = 100 27 \displaystyle = 20\cdot\frac{8}{27} - 4\cdot\frac{10}{27} - 2\cdot\frac{10}{27} = \frac{100}{27} = 20 ⋅ 27 8 − 4 ⋅ 27 10 − 2 ⋅ 27 10 = 27 100 B = f x y ′ ′ = − 3 x 2 − 2 x = − 3 ( 2 3 ) 2 − 2 ⋅ 2 3 = − 3 ⋅ 4 9 − 4 3 = − 8 3 \displaystyle B = f''_{xy} = -3x^2 - 2x = -3\left(\frac{2}{3}\right)^2 - 2\cdot\frac{2}{3} = -3\cdot\frac{4}{9} - \frac{4}{3} = -\frac{8}{3} B = f x y ′′ = − 3 x 2 − 2 x = − 3 ( 3 2 ) 2 − 2 ⋅ 3 2 = − 3 ⋅ 9 4 − 3 4 = − 3 8 C = f y y ′ ′ = 2 \displaystyle C = f''_{yy} = 2 C = f yy ′′ = 2 判断是否是极值点 A C − B 2 = 100 27 × 2 − 64 9 > 0 \displaystyle AC - B^2 = \frac{100}{27} \times 2 - \frac{64}{9} > 0 A C − B 2 = 27 100 × 2 − 9 64 > 0 A = 100 27 > 0 \displaystyle A = \frac{100}{27} > 0 A = 27 100 > 0 则 ( 2 3 , 10 27 ) \displaystyle \left(\frac{2}{3}, \frac{10}{27}\right) ( 3 2 , 27 10 ) f ( 2 3 , 10 27 ) = ( y − x 2 ) ( y − x 3 ) \displaystyle f\left(\frac{2}{3}, \frac{10}{27}\right) = (y - x^2)(y - x^3) f ( 3 2 , 27 10 ) = ( y − x 2 ) ( y − x 3 ) = ( 10 27 − 4 9 ) ( 10 27 − 8 27 ) \displaystyle = \left(\frac{10}{27} - \frac{4}{9}\right)\left(\frac{10}{27} - \frac{8}{27}\right) = ( 27 10 − 9 4 ) ( 27 10 − 27 8 ) = − 2 27 ⋅ 2 27 = − 4 27 2 \displaystyle = -\frac{2}{27} \cdot \frac{2}{27} = -\frac{4}{27^2} = − 27 2 ⋅ 27 2 = − 2 7 2 4 (19) (本题满分 12 分)Ω \Omega Ω x 2 + y 2 = 1 x^{2}+y^{2}=1 x 2 + y 2 = 1 z = 0 z=0 z = 0 x + z = 1 x+z=1 x + z = 1 Σ \displaystyle \Sigma Σ Ω \Omega Ω I = ∬ Σ 2 x z d y d z + x z cos y d z d x + 3 y z sin x d x d y \displaystyle I=\iint_{\Sigma} 2 x z \mathrm{~d} y \mathrm{~d} z+x z \cos y \mathrm{~d} z \mathrm{~d} x+3 y z \sin x \mathrm{~d} x \mathrm{~d} y I = ∬ Σ 2 x z d y d z + x z cos y d z d x + 3 yz sin x d x d y
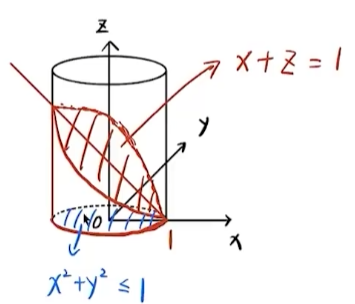
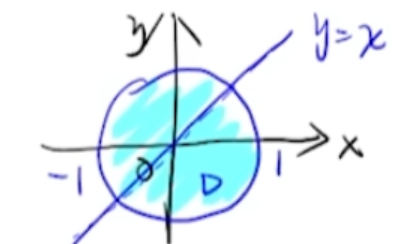
I = 原式 ∬ Σ 2 x z d y d z + x z cos y d z d x + 3 y z sin x d x d y \displaystyle I \xlongequal[]{\text{原式}} \iint_{\Sigma} 2xz \, dy \, dz + xz\cos y \, dz \, dx + 3yz\sin x \, dx \, dy I 原式 ∬ Σ 2 x z d y d z + x z cos y d z d x + 3 yz sin x d x d y = ∭ Ω ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z d v \displaystyle = \iiint_{\Omega} \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \, dv = ∭ Ω ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R d v = 高斯 ∭ Ω 2 z − x z sin y + 3 y sin x d v \displaystyle \xlongequal[]{\text{高斯}}\iiint_{\Omega} 2z - xz\sin y + 3y\sin x \, dv 高斯 ∭ Ω 2 z − x z sin y + 3 y sin x d v → x ≥ sin y 与 3 y sin x 是奇函数 ∭ Ω 2 z d v \displaystyle \xrightarrow[]{x \geq \sin y \text{与}3 y \sin x\text{是奇函数}} \iiint_{\Omega} 2z \, dv x ≥ s i n y 与 3 y s i n x 是奇函数 ∭ Ω 2 z d v = 柱线法 ∬ Σ d x d y ∫ 0 1 − x 2 z d z \displaystyle \xlongequal[]{\text{柱线法}}\iint_{\Sigma} dx \, dy \int_{0}^{1-x} 2z \, dz 柱线法 ∬ Σ d x d y ∫ 0 1 − x 2 z d z = z 2 ∣ 0 1 − x ∬ x 2 + y 2 ≤ 1 ( 1 − x ) 2 d x d y \displaystyle \xlongequal[]{\left.z^2\right|_0 ^{1-x}}\iint_{x^2 + y^2 \leq 1} (1-x)^2 \, dx \, dy z 2 ∣ 0 1 − x ∬ x 2 + y 2 ≤ 1 ( 1 − x ) 2 d x d y = 完全平方 ∬ x 2 + y 2 ≤ 1 ( 1 + x 2 − 2 x ) d x d y \displaystyle \xlongequal[]{\text{完全平方}}\iint_{x^2 + y^2 \leq 1} (1 + x^2 - 2x) \, dx \, dy 完全平方 ∬ x 2 + y 2 ≤ 1 ( 1 + x 2 − 2 x ) d x d y = ∬ D ( 1 + x 2 − 2 x ) d x d y \displaystyle = \iint_{D} (1 + x^2 - 2x) \, dx \, dy = ∬ D ( 1 + x 2 − 2 x ) d x d y = x 是奇函数 ∬ D d x d y + ∬ D x 2 d x d y → ∬ D y 2 d x d y \displaystyle \xlongequal[]{x\text{是奇函数}}\iint_{D} dx \, dy + \iint_{D} x^2 \, dx \, dy \xrightarrow[]{\iint_D y^2 d x d y} x 是奇函数 ∬ D d x d y + ∬ D x 2 d x d y ∬ D y 2 d x d y = 然后极坐标求解 轮转对称性 π + 1 2 ∬ D ( x 2 + y 2 ) d x d y \displaystyle \xlongequal[\text{然后极坐标求解}]{\text{轮转对称性}}\pi + \frac{1}{2} \iint_{D} (x^2 + y^2) \, dx \, dy 轮转对称性 然后极坐标求解 π + 2 1 ∬ D ( x 2 + y 2 ) d x d y = x 2 + y 2 = r 2 化为极坐标 π + 1 2 ∫ 0 2 π d θ ∫ 0 1 r 2 ⋅ r d r \displaystyle \xlongequal[x^2 + y^2=r^2]{\text{化为极坐标}}\pi + \frac{1}{2} \int_{0}^{2\pi} d\theta \int_{0}^{1} r^2 \cdot r \, dr 化为极坐标 x 2 + y 2 = r 2 π + 2 1 ∫ 0 2 π d θ ∫ 0 1 r 2 ⋅ r d r = π + 1 2 ⋅ 2 π ⋅ 1 4 4 = 5 π 4 \displaystyle = \pi + \frac{1}{2} \cdot 2\pi \cdot \frac{1^4}{4} = \frac{5\pi}{4} = π + 2 1 ⋅ 2 π ⋅ 4 1 4 = 4 5 π (20) (本题满分 12 分)f ( x ) f(x) f ( x ) [ − a , a ] [-a, a] [ − a , a ] f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 ξ ∈ ( − a , a ) \xi \in(-a, a) ξ ∈ ( − a , a ) f ′ ′ ( ξ ) = 1 a 2 [ f ( a ) + f ( − a ) ] f^{\prime \prime}(\xi)=\frac{1}{a^{2}}[f(a)+f(-a)] f ′′ ( ξ ) = a 2 1 [ f ( a ) + f ( − a )] f ( x ) f(x) f ( x ) ( − a , a ) (-a, a) ( − a , a ) η ∈ ( − a , a ) \eta \in(-a, a) η ∈ ( − a , a )
∣ f ′ ′ ( η ) ∣ ⩾ 1 2 a 2 ∣ f ( a ) − f ( − a ) ∣ . \left|f^{\prime \prime}(\eta)\right| \geqslant \frac{1}{2 a^{2}}|f(a)-f(-a)| . ∣ f ′′ ( η ) ∣ ⩾ 2 a 2 1 ∣ f ( a ) − f ( − a ) ∣. 带拉格朗日型余项的一阶泰勒公式 设函数 f ( x ) f(x) f ( x ) [ a , b ] [a, b] [ a , b ] 具有二阶导数 , c c c ( a , b ) (a, b) ( a , b ) f ( x ) f(x) f ( x ) x = c x=c x = c f ( x ) = f ( c ) + f ′ ( c ) ( x − c ) + f ′ ′ ( ξ ) 2 ! ( x − c ) 2 , f(x)=f(c)+f^{\prime}(c)(x-c)+\frac{f^{\prime \prime}(\xi)}{2!}(x-c)^2, f ( x ) = f ( c ) + f ′ ( c ) ( x − c ) + 2 ! f ′′ ( ξ ) ( x − c ) 2 , 其中 ξ \xi ξ x x x c c c 展开位置:中间点(左右界限相加除以二),左右端点,题中给的特殊点 解 (1) 由题设, 根据一阶带拉格朗日余项的泰勒公式, 存在 x 1 ∈ ( − a , 0 ) , x 2 ∈ ( 0 , a ) x_1 \in(-a, 0), x_2 \in(0, a) x 1 ∈ ( − a , 0 ) , x 2 ∈ ( 0 , a ) 在0点展开:f ( x ) = f ( 0 ) + f ′ ( 0 ) x + 1 2 f ′ ′ ( ξ ) x 2 \displaystyle f(x) = f(0) + f'(0)x + \frac{1}{2} f''(\xi)x^2 f ( x ) = f ( 0 ) + f ′ ( 0 ) x + 2 1 f ′′ ( ξ ) x 2 f ( − a ) = f ( 0 ) − f ′ ( 0 ) a + 1 2 f ′ ′ ( x 1 ) a 2 = f ( 0 ) = 0 − f ′ ( 0 ) a + 1 2 f ′ ′ ( x 1 ) a 2 , \displaystyle f(-a)=f(0)-f^{\prime}(0) a+\frac{1}{2} f^{\prime \prime}\left(x_1\right) a^2\xlongequal[]{f(0)=0}-f^{\prime}(0) a+\frac{1}{2} f^{\prime \prime}\left(x_1\right) a^2, f ( − a ) = f ( 0 ) − f ′ ( 0 ) a + 2 1 f ′′ ( x 1 ) a 2 f ( 0 ) = 0 − f ′ ( 0 ) a + 2 1 f ′′ ( x 1 ) a 2 , f ( a ) = f ( 0 ) + f ′ ( 0 ) a + 1 2 f ′ ′ ( x 2 ) a 2 = f ( 0 ) = 0 f ′ ( 0 ) a + 1 2 f ′ ′ ( x 2 ) a 2 . \displaystyle f(a)=f(0)+f^{\prime}(0) a+\frac{1}{2} f^{\prime \prime}\left(x_2\right) a^2\xlongequal[]{f(0)=0}f^{\prime}(0) a+\frac{1}{2} f^{\prime \prime}\left(x_2\right) a^2 . f ( a ) = f ( 0 ) + f ′ ( 0 ) a + 2 1 f ′′ ( x 2 ) a 2 f ( 0 ) = 0 f ′ ( 0 ) a + 2 1 f ′′ ( x 2 ) a 2 . 所以 f ( − a ) + f ( a ) = a 2 2 [ f ′ ′ ( x 1 ) + f ′ ′ ( x 2 ) ] f(-a)+f(a)=\frac{a^2}{2}\left[f^{\prime \prime}\left(x_1\right)+f^{\prime \prime}\left(x_2\right)\right] f ( − a ) + f ( a ) = 2 a 2 [ f ′′ ( x 1 ) + f ′′ ( x 2 ) ] 因为 f ′ ′ ( x ) f^{\prime \prime}(x) f ′′ ( x ) ξ ∈ [ x 1 , x 2 ] ⊂ ( − a , a ) \xi \in\left[x_1, x_2\right] \subset(-a, a) ξ ∈ [ x 1 , x 2 ] ⊂ ( − a , a ) f ′ ′ ( ξ ) = 平均值 1 2 [ f ′ ′ ( x 1 ) + f ′ ′ ( x 2 ) ] . f^{\prime \prime}(\xi)\xlongequal[]{\text{平均值}}\frac{1}{2}\left[f^{\prime \prime}\left(x_1\right)+f^{\prime \prime}\left(x_2\right)\right] . f ′′ ( ξ ) 平均值 2 1 [ f ′′ ( x 1 ) + f ′′ ( x 2 ) ] . 综上,存在 ξ ∈ ( − a , a ) \xi \in(-a, a) ξ ∈ ( − a , a ) f ′ ′ ( ξ ) = 1 a 2 [ f ( a ) + f ( − a ) ] . f^{\prime \prime}(\xi)=\frac{1}{a^2}[f(a)+f(-a)] . f ′′ ( ξ ) = a 2 1 [ f ( a ) + f ( − a )] . (2) (2) 设 f ( x ) f(x) f ( x ) x 0 ∈ ( − a , a ) x_0 \in(-a, a) x 0 ∈ ( − a , a ) → 极值点处导数为 0 f ′ ( x 0 ) = 0 \xrightarrow[]{\text{极值点处导数为}0}f^{\prime}\left(x_0\right)=0 极值点处导数为 0 f ′ ( x 0 ) = 0 根据一阶带拉格朗日余项的泰勒公式, 存在 b ∈ ( − a , x 0 ) , c ∈ ( x 0 , a ) b \in\left(-a, x_0\right), c \in\left(x_0, a\right) b ∈ ( − a , x 0 ) , c ∈ ( x 0 , a ) f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 f ′ ′ ( η ) ( x − x 0 ) 2 , η \displaystyle f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2} f''(\eta)(x - x_0)^2, \quad \eta f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 2 1 f ′′ ( η ) ( x − x 0 ) 2 , η x x x x 0 x_0 x 0 . . . f ( − a ) = f ( x 0 ) − f ′ ( x 0 ) ( a + x 0 ) + 1 2 f ′ ′ ( b ) ( a + x 0 ) 2 = f ( x 0 ) + 1 2 f ′ ′ ( b ) ( a + x 0 ) 2 , \displaystyle f(-a)=f\left(x_0\right)-f^{\prime}\left(x_0\right)\left(a+x_0\right)+\frac{1}{2} f^{\prime \prime}(b)\left(a+x_0\right)^2=f\left(x_0\right)+\frac{1}{2} f^{\prime \prime}(b)\left(a+x_0\right)^2, f ( − a ) = f ( x 0 ) − f ′ ( x 0 ) ( a + x 0 ) + 2 1 f ′′ ( b ) ( a + x 0 ) 2 = f ( x 0 ) + 2 1 f ′′ ( b ) ( a + x 0 ) 2 , f ( a ) = f ( x 0 ) + f ′ ( x 0 ) ( a − x 0 ) + 1 2 f ′ ′ ( c ) ( a − x 0 ) 2 = f ( x 0 ) + 1 2 f ′ ′ ( c ) ( a − x 0 ) 2 . \displaystyle f(a)=f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(a-x_0\right)+\frac{1}{2} f^{\prime \prime}(c)\left(a-x_0\right)^2=f\left(x_0\right)+\frac{1}{2} f^{\prime \prime}(c)\left(a-x_0\right)^2 . f ( a ) = f ( x 0 ) + f ′ ( x 0 ) ( a − x 0 ) + 2 1 f ′′ ( c ) ( a − x 0 ) 2 = f ( x 0 ) + 2 1 f ′′ ( c ) ( a − x 0 ) 2 . 所以 f ( a ) − f ( − a ) = 1 2 [ f ′ ′ ( c ) ( a − x 0 ) 2 − f ′ ′ ( b ) ( a + x 0 ) 2 ] f(a)-f(-a)=\frac{1}{2}\left[f^{\prime \prime}(c)\left(a-x_0\right)^2-f^{\prime \prime}(b)\left(a+x_0\right)^2\right] f ( a ) − f ( − a ) = 2 1 [ f ′′ ( c ) ( a − x 0 ) 2 − f ′′ ( b ) ( a + x 0 ) 2 ] 不妨设 ∣ f ′ ′ ( b ) ∣ ⩽ ∣ f ′ ′ ( c ) ∣ \left|f^{\prime \prime}(b)\right| \leqslant\left|f^{\prime \prime}(c)\right| ∣ f ′′ ( b ) ∣ ⩽ ∣ f ′′ ( c ) ∣ η = c \eta=c η = c ∣ f ( a ) − f ( − a ) ∣ ⩽ 1 2 ∣ f ′ ′ ( η ) ∣ [ ( a − x 0 ) 2 + ( a + x 0 ) 2 ] ⩽ 2 a 2 ∣ f ′ ′ ( η ) ∣ . |f(a)-f(-a)| \leqslant \frac{1}{2}\left|f^{\prime \prime}(\eta)\right|\left[\left(a-x_0\right)^2+\left(a+x_0\right)^2\right] \leqslant 2 a^2\left|f^{\prime \prime}(\eta)\right| . ∣ f ( a ) − f ( − a ) ∣ ⩽ 2 1 ∣ f ′′ ( η ) ∣ [ ( a − x 0 ) 2 + ( a + x 0 ) 2 ] ⩽ 2 a 2 ∣ f ′′ ( η ) ∣ . 综上, 存在 η ∈ ( − a , a ) \eta \in(-a, a) η ∈ ( − a , a ) ∣ f ′ ′ ( η ) ∣ ⩾ 1 2 a 2 ∣ f ( a ) − f ( − a ) ∣ . \left|f^{\prime \prime}(\eta)\right| \geqslant \frac{1}{2 a^2}|f(a)-f(-a)| . ∣ f ′′ ( η ) ∣ ⩾ 2 a 2 1 ∣ f ( a ) − f ( − a ) ∣. (2)高昆仑版 (2) 设 f ( x ) f(x) f ( x ) x 0 ∈ ( − a , a ) x_0 \in(-a, a) x 0 ∈ ( − a , a ) f ′ ( x 0 ) = 0 f^{\prime}\left(x_0\right)=0 f ′ ( x 0 ) = 0
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 f ′ ′ ( τ ) ( x − x 0 ) 2 \displaystyle f(x) =f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)+\frac{1}{2} f^{\prime \prime}(\tau)\left(x-x_0\right)^2 f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 2 1 f ′′ ( τ ) ( x − x 0 ) 2 = f ′ ( x 0 ) = 0 f ( x 0 ) + 1 2 f ′ ′ ( τ ) ( x − x 0 ) 2 . \displaystyle \xlongequal[]{f^{\prime}\left(x_0\right)=0}f\left(x_0\right)+\frac{1}{2} f^{\prime \prime}(\tau)\left(x-x_0\right)^2 . f ′ ( x 0 ) = 0 f ( x 0 ) + 2 1 f ′′ ( τ ) ( x − x 0 ) 2 . 取 x = − a \displaystyle x = -a x = − a f ( − a ) = f ( x 0 ) + 1 2 f ′ ′ ( η 1 ) ( − a − x 0 ) 2 . \displaystyle f(-a) = f(x_0) + \frac{1}{2} f''(\eta_1)(-a - x_0)^2. f ( − a ) = f ( x 0 ) + 2 1 f ′′ ( η 1 ) ( − a − x 0 ) 2 . 取 x = a \displaystyle x = a x = a f ( a ) = f ( x 0 ) + 1 2 f ′ ′ ( η 2 ) ( a − x 0 ) 2 . \displaystyle f(a) = f(x_0) + \frac{1}{2} f''(\eta_2)(a - x_0)^2. f ( a ) = f ( x 0 ) + 2 1 f ′′ ( η 2 ) ( a − x 0 ) 2 . 以上两式相减,得f ( − a ) − f ( a ) = 1 2 f ′ ′ ( η 1 ) ( a + x 0 ) 2 − 1 2 f ′ ′ ( η 2 ) ( a − x 0 ) 2 . \displaystyle f(-a) - f(a) = \frac{1}{2} f''(\eta_1)(a + x_0)^2 - \frac{1}{2} f''(\eta_2)(a - x_0)^2. f ( − a ) − f ( a ) = 2 1 f ′′ ( η 1 ) ( a + x 0 ) 2 − 2 1 f ′′ ( η 2 ) ( a − x 0 ) 2 . 于是∣ f ( − a ) − f ( a ) ∣ = ∣ 1 2 f ′ ′ ( η 1 ) ( a + x 0 ) 2 − 1 2 f ′ ′ ( η 2 ) ( a − x 0 ) 2 ∣ \displaystyle |f(-a) - f(a)| = \left| \frac{1}{2} f''(\eta_1)(a + x_0)^2 - \frac{1}{2} f''(\eta_2)(a - x_0)^2 \right| ∣ f ( − a ) − f ( a ) ∣ = 2 1 f ′′ ( η 1 ) ( a + x 0 ) 2 − 2 1 f ′′ ( η 2 ) ( a − x 0 ) 2 → ∣ a ± b ∣ ⩽ ∣ a ∣ + ∣ b ∣ ≤ ∣ 1 2 f ′ ′ ( η 1 ) ( a + x 0 ) 2 ∣ + ∣ 1 2 f ′ ′ ( η 2 ) ( a − x 0 ) 2 ∣ . \displaystyle \xrightarrow[]{|a \pm b| \leqslant|a|+|b|}\leq \left| \frac{1}{2} f''(\eta_1)(a + x_0)^2 \right| + \left| \frac{1}{2} f''(\eta_2)(a - x_0)^2 \right|. ∣ a ± b ∣ ⩽ ∣ a ∣ + ∣ b ∣ ≤ 2 1 f ′′ ( η 1 ) ( a + x 0 ) 2 + 2 1 f ′′ ( η 2 ) ( a − x 0 ) 2 . → ∣ f ′ ′ ( η ) ∣ = max { ∣ f ′ ′ ( η 1 ) ∣ , ∣ f ′ ′ ( η 2 ) ∣ } ≤ 1 2 ∣ f ′ ′ ( η ) ∣ ⋅ [ ( a + x 0 ) 2 + ( a − x 0 ) 2 ] \displaystyle \xrightarrow[]{\left|f''(\eta)\right| = \max\left\{\left|f''(\eta_1)\right|, \left|f''(\eta_2)\right|\right\} }\leq \frac{1}{2} \left|f''(\eta)\right| \cdot \left[(a + x_0)^2 + (a - x_0)^2\right] ∣ f ′′ ( η ) ∣ = m a x { ∣ f ′′ ( η 1 ) ∣ , ∣ f ′′ ( η 2 ) ∣ } ≤ 2 1 ∣ f ′′ ( η ) ∣ ⋅ [ ( a + x 0 ) 2 + ( a − x 0 ) 2 ] = 完全平方展开后整理 1 2 ∣ f ′ ′ ( η ) ∣ ⋅ ( 2 a 2 + 2 x 0 2 ) \displaystyle \xlongequal[]{\text{完全平方展开后整理}}\frac{1}{2} \left|f''(\eta)\right| \cdot (2a^2 + 2x_0^2) 完全平方展开后整理 2 1 ∣ f ′′ ( η ) ∣ ⋅ ( 2 a 2 + 2 x 0 2 ) → x 0 2 < a 2 < 1 2 ∣ f ′ ′ ( η ) ∣ ⋅ 4 a 2 = 2 a 2 ∣ f ′ ′ ( η ) ∣ . \displaystyle \xrightarrow[]{x_0^2<a^2}< \frac{1}{2} \left|f''(\eta)\right| \cdot 4a^2 = 2a^2 \left|f''(\eta)\right|. x 0 2 < a 2 < 2 1 ∣ f ′′ ( η ) ∣ ⋅ 4 a 2 = 2 a 2 ∣ f ′′ ( η ) ∣ . 所以∣ f ′ ′ ( η ) ∣ > ∣ f ( − a ) − f ( a ) ∣ 2 a 2 . \displaystyle \left|f''(\eta)\right| > \frac{\left|f(-a) - f(a)\right|}{2a^2}. ∣ f ′′ ( η ) ∣ > 2 a 2 ∣ f ( − a ) − f ( a ) ∣ . (21) (本题满分 12 分)
f ( x 1 , x 2 , x 3 ) = x 1 2 + 2 x 2 2 + 2 x 3 2 + 2 x 1 x 2 − 2 x 1 x 3 , \displaystyle f\left(x_{1}, x_{2}, x_{3}\right)=x_{1}^{2}+2 x_{2}^{2}+2 x_{3}^{2}+2 x_{1} x_{2}-2 x_{1} x_{3}, f ( x 1 , x 2 , x 3 ) = x 1 2 + 2 x 2 2 + 2 x 3 2 + 2 x 1 x 2 − 2 x 1 x 3 , g ( y 1 , y 2 , y 3 ) = y 1 2 + y 2 2 + y 3 2 + 2 y 2 y 3 . \displaystyle g\left(y_{1}, y_{2}, y_{3}\right)=y_{1}^{2}+y_{2}^{2}+y_{3}^{2}+2 y_{2} y_{3} . g ( y 1 , y 2 , y 3 ) = y 1 2 + y 2 2 + y 3 2 + 2 y 2 y 3 . x = P y \boldsymbol{x}=\boldsymbol{P} \boldsymbol{y} x = P y f ( x 1 , x 2 , x 3 ) f\left(x_{1}, x_{2}, x_{3}\right) f ( x 1 , x 2 , x 3 ) g ( y 1 , y 2 , y 3 ) g\left(y_{1}, y_{2}, y_{3}\right) g ( y 1 , y 2 , y 3 ) x = Q y \boldsymbol{x}=\boldsymbol{Q y} x = Qy f ( x 1 , x 2 , x 3 ) f\left(x_{1}, x_{2}, x_{3}\right) f ( x 1 , x 2 , x 3 ) g ( y 1 , y 2 , y 3 ) g\left(y_{1}, y_{2}, y_{3}\right) g ( y 1 , y 2 , y 3 ) 合同变换 设 A \boldsymbol{A} A n n n P \boldsymbol{P} P n n n P T A P \boldsymbol{P}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{P} P T A P A \boldsymbol{A} A B = P T A P \boldsymbol{B}=\boldsymbol{P}^{\mathrm{T}} \boldsymbol{A P} B = P T AP A \boldsymbol{A} A f = x ⊤ A x = x = p y y ⊤ p ⊤ A p y = g f=x^{\top} A x \xlongequal[]{x=p y} y^{\top} p^{\top} A p y=g f = x ⊤ A x x = p y y ⊤ p ⊤ A p y = g 方法1 f和g具有相同的规范型 f → x = P 1 z h P 1 T A P 1 = Λ \displaystyle f \xrightarrow{x=P_1z} h \quad P_1^TAP_1 = \Lambda f x = P 1 z h P 1 T A P 1 = Λ g → y = P 2 z h P 2 T B P 2 = Λ \displaystyle g \xrightarrow{y=P_2z} h \quad P_2^TBP_2 = \Lambda g y = P 2 z h P 2 T B P 2 = Λ B = ( P 2 T ) − 1 Λ P 2 − 1 = ( P 2 − 1 ) T P 1 T A P 1 P 2 − 1 \displaystyle B = (P_2^T)^{-1} \Lambda P_2^{-1} = (P_2^{-1})^T P_1^T A P_1 P_2^{-1} B = ( P 2 T ) − 1 Λ P 2 − 1 = ( P 2 − 1 ) T P 1 T A P 1 P 2 − 1 记 P = P 1 P 2 − 1 \displaystyle P = P_1 P_2^{-1} P = P 1 P 2 − 1 B = P T A P \displaystyle B = P^T A P B = P T A P A = ( 11 − 1 120 − 102 ) B = ( 100 011 011 ) \displaystyle A=\left(\begin{array}{ccc}1 1 -1 \\1 2 0 \\-1 0 2\end{array}\right) \quad B=\left(\begin{array}{lll}1 0 0 \\0 1 1 \\0 1 1\end{array}\right) A = 11 − 1 120 − 102 B = 100 011 011 A = ( 11 − 1 120 − 102 ) → r 2 − r 1 ( 11 − 1 011 − 102 ) → C 2 − C 1 ( 10 − 1 011 − 112 ) \displaystyle A=\left(\begin{array}{ccc}1 1 -1 \\1 2 0 \\-1 0 2\end{array}\right) \xrightarrow{r_2-r_1}\left(\begin{array}{ccc}1 1 -1 \\0 1 1 \\-1 0 2\end{array}\right) \xrightarrow{C_2-C_1}\left(\begin{array}{ccc}1 0 -1 \\0 1 1 \\-1 1 2\end{array}\right) A = 11 − 1 120 − 102 r 2 − r 1 11 − 1 011 − 102 C 2 − C 1 10 − 1 011 − 112 → r 3 + r 1 ( 10 − 1 011 011 ) → C 3 + C 1 ( 100 011 011 ) \displaystyle \xrightarrow{r_3+r_1} \left(\begin{array}{ccc}1 0 -1 \\0 1 1 \\0 1 1\end{array}\right) \xrightarrow{C_3+C_1}\left(\begin{array}{ccc}1 0 0 \\0 1 1 \\0 1 1\end{array}\right) r 3 + r 1 10 − 1 011 011 C 3 + C 1 100 011 011 P 1 = ( 1 − 10 010 001 ) P 2 = ( 101 010 001 ) \displaystyle P_1=\left(\begin{array}{ccc}1 -1 0 \\0 1 0 \\0 0 1\end{array}\right) \quad P_2=\left(\begin{array}{lll}1 0 1 \\0 1 0 \\0 0 1\end{array}\right) \quad P 1 = 1 − 10 010 001 P 2 = 101 010 001 P = P 1 P 2 = ( 1 − 10 010 001 ) ( 101 010 001 ) = ( 1 − 11 010 001 ) \displaystyle P=P_1 P_2=\left(\begin{array}{ccc}1 -1 0 \\0 1 0 \\0 0 1\end{array}\right)\left(\begin{array}{lll}1 0 1 \\0 1 0 \\0 0 1\end{array}\right)=\left(\begin{array}{ccc}1 -1 1 \\0 1 0 \\0 0 1\end{array}\right) P = P 1 P 2 = 1 − 10 010 001 101 010 001 = 1 − 11 010 001 方法2 解:(1)
f ( x 1 , x 2 , x 3 ) = x 1 2 + 2 x 2 2 + 2 x 3 2 + 2 x 1 x 2 − 2 x 1 x 3 \displaystyle f(x_1, x_2, x_3) = x_1^2 + 2x_2^2 + 2x_3^2 + 2x_1x_2 - 2x_1x_3 f ( x 1 , x 2 , x 3 ) = x 1 2 + 2 x 2 2 + 2 x 3 2 + 2 x 1 x 2 − 2 x 1 x 3 = ( x 1 + x 2 − x 3 ) 2 + x 2 2 + x 3 2 + 2 x 2 x 3 \displaystyle = (x_1 + x_2 - x_3)^2 + x_2^2 + x_3^2 + 2x_2x_3 = ( x 1 + x 2 − x 3 ) 2 + x 2 2 + x 3 2 + 2 x 2 x 3 = ( x 1 + x 2 − x 3 ) 2 + ( x 2 + x 3 ) 3 + 0 x 3 2 . \displaystyle = (x_1 + x_2 - x_3)^2 + (x_2 + x_3)^3 + 0x_3^2. = ( x 1 + x 2 − x 3 ) 2 + ( x 2 + x 3 ) 3 + 0 x 3 2 . { x 1 + x 2 − x 3 = z 1 x 2 + x 3 = z 2 x 3 = z 3 \displaystyle \begin{array}{l}\left\{\begin{array}{l}x_{1} + x_{2} - x_{3} = z_{1} \\x_{2} + x_{3} = z_{2} \\x_{3} = z_{3}\end{array}\right.\end{array} ⎩ ⎨ ⎧ x 1 + x 2 − x 3 = z 1 x 2 + x 3 = z 2 x 3 = z 3 g ( y 1 , y 2 , y 3 ) = y 1 2 + y 2 2 + y 3 2 + 2 y 2 y 3 = y 1 2 + ( y 2 + y 3 ) 2 + 0 y 3 2 . \displaystyle g(y_1, y_2, y_3) = y_1^2 + y_2^2 + y_3^2 + 2y_2y_3 = y_1^2 + (y_2 + y_3)^2 + 0y_3^2. g ( y 1 , y 2 , y 3 ) = y 1 2 + y 2 2 + y 3 2 + 2 y 2 y 3 = y 1 2 + ( y 2 + y 3 ) 2 + 0 y 3 2 . { y 1 = z 1 y 2 + y 3 = z 2 \displaystyle \begin{array}{l}\left\{\begin{array}{l}y_{1} = z_{1} \\y_{2} + y_{3} = z_{2}\end{array}\right.\end{array} { y 1 = z 1 y 2 + y 3 = z 2 则 g ( y 1 , y 2 , y 3 ) = z 1 2 + z 2 2 + 0 z 3 2 \displaystyle g(y_{1}, y_{2}, y_{3}) = z_{1}^{2} + z_{2}^{2} + 0z_{3}^{2} g ( y 1 , y 2 , y 3 ) = z 1 2 + z 2 2 + 0 z 3 2 (1) =(2),得{ x 1 + x 2 − x 3 = y 1 x 2 + x 3 = y 2 + y 3 x 3 = y 3 \displaystyle \left\{\begin{array}{l}x_{1} + x_{2} - x_{3} = y_{1} \\x_{2} + x_{3} = y_{2} + y_{3} \\x_{3} = y_{3}\end{array}\right. ⎩ ⎨ ⎧ x 1 + x 2 − x 3 = y 1 x 2 + x 3 = y 2 + y 3 x 3 = y 3 即{ x 1 = y 1 − y 2 + y 3 x 2 = y 2 x 3 = y 3 \displaystyle \left\{\begin{array}{l}x_{1} = y_{1} - y_{2} + y_{3} \\x_{2} = y_{2} \\x_{3} = y_{3}\end{array}\right. ⎩ ⎨ ⎧ x 1 = y 1 − y 2 + y 3 x 2 = y 2 x 3 = y 3 记 P = [ 1 − 11 010 001 ] \displaystyle P = \begin{bmatrix} 1 -1 1 \\ 0 1 0 \\ 0 0 1 \end{bmatrix} P = 1 − 11 010 001 x = P y \displaystyle x = P y x = P y f ( x 1 , x 2 , x 3 ) = g ( y 1 , y 2 , y 3 ) \displaystyle f(x_1, x_2, x_3) = g(y_1, y_2, y_3) f ( x 1 , x 2 , x 3 ) = g ( y 1 , y 2 , y 3 ) (2) 二次型 f ( x 1 , x 2 , x 3 ) \displaystyle f(x_1, x_2, x_3) f ( x 1 , x 2 , x 3 ) g ( y 1 , y 2 , y 3 ) \displaystyle g(y_1, y_2, y_3) g ( y 1 , y 2 , y 3 )
A = ( 11 − 1 120 − 102 ) , B = ( 100 011 011 ) . \displaystyle A = \begin{pmatrix} 1 1 -1 \\ 1 2 0 \\ -1 0 2 \end{pmatrix}, \quad B = \begin{pmatrix} 1 0 0 \\ 0 1 1 \\ 0 1 1 \end{pmatrix}. A = 11 − 1 120 − 102 , B = 100 011 011 . 是否存在正交变换 x = Q y \displaystyle x = Q y x = Q y f \displaystyle f f g \displaystyle g g → 等价 \displaystyle \xrightarrow[]{\text{等价}} 等价 Q , Q, Q , Q T A Q = B Q^T A Q = B Q T A Q = B Q − 1 A Q = B Q^{-1} A Q = B Q − 1 A Q = B . . . 由于 tr ( A ) ≠ tr ( B ) \displaystyle \operatorname{tr}(A) \neq \operatorname{tr}(B) tr ( A ) = tr ( B ) A \displaystyle A A B \displaystyle B B 故,不存在正交变换 x = Q y \displaystyle x = Q y x = Q y f \displaystyle f f g \displaystyle g g (22) (本题满分 12 分)( X , Y ) (X, Y) ( X , Y )
f ( x , y ) = { 2 π ( x 2 + y 2 ) , x 2 + y 2 ⩽ 1 , 0 , 其他. \displaystyle f(x, y)= \begin{cases}\frac{2}{\pi}\left(x^{2}+y^{2}\right), & x^{2}+y^{2} \leqslant 1, \\ 0, & \text { 其他. }\end{cases} f ( x , y ) = { π 2 ( x 2 + y 2 ) , 0 , x 2 + y 2 ⩽ 1 , 其他 . X X X Y Y Y X X X Y Y Y Z = X 2 + Y 2 Z=X^{2}+Y^{2} Z = X 2 + Y 2 解 (1) 因为Cov ( X , Y ) = E ( X Y ) − E X E Y \operatorname{Cov}(X, Y)=E(X Y)-E X E Y Cov ( X , Y ) = E ( X Y ) − EXE Y E X = ∬ x ′ + y ′ < 1 x ⋅ 2 π ( x 2 + y 2 ) d x d y = 0 , \displaystyle E X=\iint_{x^{\prime}+y^{\prime}<1} x \cdot \frac{2}{\pi}\left(x^2+y^2\right) \mathrm{d} x \mathrm{~d} y=0, EX = ∬ x ′ + y ′ < 1 x ⋅ π 2 ( x 2 + y 2 ) d x d y = 0 , E Y = ∬ x ′ + y ′ < 1 y ⋅ 2 π ( x 2 + y 2 ) d x d y = 0 , \displaystyle E Y=\iint_{x^{\prime}+y^{\prime}<1} y \cdot \frac{2}{\pi}\left(x^2+y^2\right) \mathrm{d} x \mathrm{~d} y=0, E Y = ∬ x ′ + y ′ < 1 y ⋅ π 2 ( x 2 + y 2 ) d x d y = 0 , E ( X Y ) = ∬ x ′ + y ′ < 1 x y ⋅ 2 π ( x 2 + y 2 ) d x d y = 0 , \displaystyle E(X Y)=\iint_{x^{\prime}+y^{\prime}<1} x y \cdot \frac{2}{\pi}\left(x^2+y^2\right) \mathrm{d} x \mathrm{~d} y=0, E ( X Y ) = ∬ x ′ + y ′ < 1 x y ⋅ π 2 ( x 2 + y 2 ) d x d y = 0 , 所以 X X X Y Y Y Cov ( X , Y ) = E ( X Y ) − E X E Y = 0. \operatorname{Cov}(X, Y)=E(X Y)-E X E Y=0 . Cov ( X , Y ) = E ( X Y ) − EXE Y = 0. (2) 对 ∀ x , y \displaystyle \forall x, y ∀ x , y f ( x , y ) = f X ( x ) ⋅ f Y ( y ) \displaystyle f(x, y) = f_X(x) \cdot f_Y(y) f ( x , y ) = f X ( x ) ⋅ f Y ( y ) X \displaystyle X X Y \displaystyle Y Y 若 f ( x , y ) \displaystyle f(x, y) f ( x , y ) f X ( x ) \displaystyle f_X(x) f X ( x ) f Y ( y ) \displaystyle f_Y(y) f Y ( y ) X \displaystyle X X Y \displaystyle Y Y 若 f ( x , y ) \displaystyle f(x, y) f ( x , y ) X \displaystyle X X Y \displaystyle Y Y (3) 记 Z Z Z F Z ( z ) F_Z(z) F Z ( z ) F Z ( z ) = P { Z ≤ z } = P { X 2 + Y 2 ≤ z } \displaystyle F_Z(z) = P\{Z \leq z\} = P\{X^2 + Y^2 \leq z\} F Z ( z ) = P { Z ≤ z } = P { X 2 + Y 2 ≤ z } 0 ≤ Z ≤ 1 \displaystyle 0 \leq Z \leq 1 0 ≤ Z ≤ 1 − ∞ < z < + ∞ \displaystyle -\infty < z < +\infty − ∞ < z < + ∞ 若 z < 0 \displaystyle z < 0 z < 0 F Z ( z ) = 0 \displaystyle F_Z(z) = 0 F Z ( z ) = 0 若 z ≥ 1 \displaystyle z \geq 1 z ≥ 1 F Z ( z ) = 1 \displaystyle F_Z(z) = 1 F Z ( z ) = 1 若 0 ≤ z < 1 \displaystyle 0 \leq z < 1 0 ≤ z < 1 F Z ( z ) = P { X 2 + Y 2 ≤ z } = ∬ x 2 + y 2 ≤ z 2 π ( x 2 + y 2 ) d x d y \displaystyle F_Z(z) = P\{X^2 + Y^2 \leq z\} = \iint\limits_{x^2+y^2 \leq z} \frac{2}{\pi} (x^2 + y^2) \, dx \, dy F Z ( z ) = P { X 2 + Y 2 ≤ z } = x 2 + y 2 ≤ z ∬ π 2 ( x 2 + y 2 ) d x d y ∫ 0 2 π d θ ∫ 0 z 2 π r 3 d r = z 2 . \displaystyle \int_0^{2 \pi} \mathrm{~d} \theta \int_0^{\sqrt{z}} \frac{2}{\pi} r^3 \mathrm{~d} r=z^2 . ∫ 0 2 π d θ ∫ 0 z π 2 r 3 d r = z 2 . f Z ( z ) = { 2 z , 0 < z < 1 , 0 , 其他 . \displaystyle f_Z(z) = \begin{cases} 2z, 0 < z < 1, \\0,\text{其他}.\end{cases} f Z ( z ) = { 2 z , 0 < z < 1 , 0 , 其他 .