一、选择题 (本题共 8 小题, 每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有一项等合题目 要求,把所选项前的字母填在题后的括号内. )
(1) 当 x → 0 x \rightarrow 0 x → 0 x − tan x x-\tan x x − tan x x k x^{k} x k k = ( ) k=(\quad) k = ( )
(1) 用对tan用泰勒展开,得tan x = x + x 3 3 + o ( x 3 ) \displaystyle \tan x=x+\frac{x^3}{3}+o\left(x^3\right) tan x = x + 3 x 3 + o ( x 3 ) → 代入题式 x − tan x = − x 3 3 + o ( x 3 ) \displaystyle \xrightarrow[]{\text{代入题式}}x-\tan x=-\frac{x^3}{3}+o\left(x^3\right) 代入题式 x − tan x = − 3 x 3 + o ( x 3 ) (2) 设函数 f ( x ) = { x ∣ x ∣ , x ⩽ 0 , x ln x , x > 0 , \displaystyle f(x)=\left\{\begin{array}{ll}x|x|, & x \leqslant 0, \\ x \ln x, & x>0,\end{array}\right. f ( x ) = { x ∣ x ∣ , x ln x , x ⩽ 0 , x > 0 , x = 0 x=0 x = 0 f ( x ) f(x) f ( x ) ( ) (\quad) ( )
(2) 确定是否连续:看左右极限是否相等,是否等于函数值 f ( 0 ) = 0 \displaystyle f(0)=0 f ( 0 ) = 0 0 = 0 0=0 0 = 0 f ( 0 − ) = lim x → 0 − ( − x 2 ) = 0 \displaystyle f\left(0^{-}\right)=\lim _{x \rightarrow 0^{-}}\left(-x^2\right)=0 f ( 0 − ) = x → 0 − lim ( − x 2 ) = 0 f ( 0 + ) = lim x → 0 + x ln x = lim x → 0 + ln x 1 / x = lim x → 0 + 1 x − 1 x 2 = 0 \displaystyle f\left(0^{+}\right)=\lim _{x \rightarrow 0^{+}} x \ln x=\lim _{x \rightarrow 0^{+}} \frac{\ln x}{1 / x}=\lim _{x \rightarrow 0^{+}} \frac{\frac{1}{x}}{-\frac{1}{x^2}}=0 f ( 0 + ) = x → 0 + lim x ln x = x → 0 + lim 1/ x ln x = x → 0 + lim − x 2 1 x 1 = 0 左极限=右极限=函数值,则连续 可导必然连续,连续不一定可导 f − ′ ( 0 ) = lim x → 0 − f ( x ) − f ( 0 ) x = lim x → 0 − − x 2 x = 0 \displaystyle f_{{-}}^{\prime}(0)=\lim _{x \rightarrow 0^{-}} \frac{f(x)-f(0)}{x}=\lim _{x \rightarrow 0^{-}} \frac{-x^2}{x}=0 f − ′ ( 0 ) = x → 0 − lim x f ( x ) − f ( 0 ) = x → 0 − lim x − x 2 = 0 f + ′ ( 0 ) = lim x → 0 + x ln x x = lim x → 0 + ln x = ∞ \displaystyle f_{+}^{\prime}(0)=\lim _{x \rightarrow 0^{+}} \frac{x \ln x}{x}=\lim _{x \rightarrow 0^{+}} \ln x=\infty f + ′ ( 0 ) = x → 0 + lim x x ln x = x → 0 + lim ln x = ∞ 左右导数不相等,则不可导 通过画图来判断函数f(x)是否是极值点 { − δ < x < 0 时 , f ( x ) = x ∣ x ∣ < 0 0 < x < δ 时 , f ( x ) = x ln x < 0 \displaystyle \begin{aligned} \begin{cases}-\delta < x < 0 \text{时}, f(x) = x|x| < 0 \\0 < x < \delta \text{时}, f(x) = x\ln x < 0\end{cases} \end{aligned} { − δ < x < 0 时 , f ( x ) = x ∣ x ∣ < 0 0 < x < δ 时 , f ( x ) = x ln x < 0 于是 x ∈ ( − δ , δ ) \displaystyle \begin{aligned} x \in (-\delta, \delta) \end{aligned} x ∈ ( − δ , δ ) f ( x ) < f ( 0 ) \displaystyle \begin{aligned} f(x) < f(0) \end{aligned} f ( x ) < f ( 0 ) 答 应选 B. (3) 设 { u n } \left\{u_{n}\right\} { u n } ( ) (\quad) ( ) ∑ n = 1 ∞ u n n \displaystyle \sum_{n=1}^{\infty} \frac{u_{n}}{n} n = 1 ∑ ∞ n u n ∑ n = 1 ∞ ( − 1 ) n 1 u n \displaystyle \sum_{n=1}^{\infty}(-1)^{n} \frac{1}{u_{n}} n = 1 ∑ ∞ ( − 1 ) n u n 1 ∑ n = 1 ∞ ( 1 − u n u n + 1 ) \displaystyle \sum_{n=1}^{\infty}\left(1-\frac{u_{n}}{u_{n+1}}\right) n = 1 ∑ ∞ ( 1 − u n + 1 u n ) ∑ n = 1 ∞ ( u n + 1 2 − u n 2 ) \displaystyle \sum_{n=1}^{\infty}\left(u_{n+1}^{2}-u_{n}^{2}\right) n = 1 ∑ ∞ ( u n + 1 2 − u n 2 )
(3) 答 应选 D.解 级数收敛的定义 若级数 ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_n n = 1 ∑ ∞ a n { s n } \left\{s_n\right\} { s n } s s s lim n → ∞ s n = s \displaystyle \lim _{n \rightarrow \infty} s_n=s n → ∞ lim s n = s ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_n n = 1 ∑ ∞ a n s s s 若 { s n } \left\{s_n\right\} { s n } ∑ n = 1 ∞ a n \displaystyle \sum_{n=1}^{\infty} a_n n = 1 ∑ ∞ a n 排除法 选项 A:∑ n = 1 ∞ u n n \displaystyle \sum_{n=1}^{\infty} \frac{u_{n}}{n} n = 1 ∑ ∞ n u n 取 u n = 1 − 1 n u_n=1-\frac{1}{n} u n = 1 − n 1 则 u n n = 1 n − 1 n 2 \frac{u_n}{n}=\frac{1}{n}-\frac{1}{n^2} n u n = n 1 − n 2 1 由于 ∑ n = 1 ∞ 1 n \displaystyle \sum_{n=1}^{\infty} \frac{1}{n} n = 1 ∑ ∞ n 1 ∑ n = 1 ∞ 1 n 2 \displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2} n = 1 ∑ ∞ n 2 1 ∑ n = 1 ∞ ( 1 n − 1 n 2 ) \displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n^2}\right) n = 1 ∑ ∞ ( n 1 − n 2 1 ) 选项 A 不正确. 选项 B:∑ n = 1 ∞ ( − 1 ) n 1 u n \displaystyle \sum_{n=1}^{\infty}(-1)^{n} \frac{1}{u_{n}} n = 1 ∑ ∞ ( − 1 ) n u n 1 取 u n = − 1 n u_n=-\frac{1}{n} u n = − n 1 ( − 1 ) n 1 u n = ( − 1 ) n + 1 n , (-1)^n \frac{1}{u_n}=(-1)^{n+1} n, ( − 1 ) n u n 1 = ( − 1 ) n + 1 n , ( − 1 ) n + 1 n \displaystyle (-1)^{n+1} n ( − 1 ) n + 1 n ∑ n = 1 ∞ ( − 1 ) n 1 u n \displaystyle \sum_{n=1}^{\infty}(-1)^n \frac{1}{u_n} n = 1 ∑ ∞ ( − 1 ) n u n 1 选项 B不正确 选项C: ∑ n = 1 ∞ ( 1 − u n u n + 1 ) \displaystyle \sum_{n=1}^{\infty}\left(1-\frac{u_{n}}{u_{n+1}}\right) n = 1 ∑ ∞ ( 1 − u n + 1 u n ) 取 u n = − 1 n u_n=-\frac{1}{n} u n = − n 1 1 − u n u n + 1 = 1 − n + 1 n = − 1 n 1-\frac{u_n}{u_{n+1}}=1-\frac{n+1}{n}=-\frac{1}{n} 1 − u n + 1 u n = 1 − n n + 1 = − n 1 − 1 n \displaystyle -\frac{1}{n} − n 1 ∑ n = 1 ∞ ( 1 − u n u n + 1 ) \displaystyle \sum_{n=1}^{\infty}\left(1-\frac{u_n}{u_{n+1}}\right) n = 1 ∑ ∞ ( 1 − u n + 1 u n ) 选项C 不正确. 由排除法可知, 应选 D. 由于 u n + 1 2 − u n 2 = ( u n + 1 + u n ) ( u n + 1 − u n ) u_{n+1}^2-u_n^2=\left(u_{n+1}+u_n\right)\left(u_{n+1}-u_n\right) u n + 1 2 − u n 2 = ( u n + 1 + u n ) ( u n + 1 − u n ) { u n } \left\{u_n\right\} { u n } 故存在正数 M M M ∣ u n + 1 2 − u n 2 ∣ ⩽ 2 M ∣ u n + 1 − u n ∣ = u n 单调增加 2 M ( u n + 1 − u n ) \displaystyle \left|u_{n+1}^2-u_n^2\right| \leqslant 2 M\left|u_{n+1}-u_n\right| \xlongequal{u_n \text{ 单调增加 }} 2 M\left(u_{n+1}-u_n\right) u n + 1 2 − u n 2 ⩽ 2 M ∣ u n + 1 − u n ∣ u n 单调增加 2 M ( u n + 1 − u n ) s n = ∑ k = 1 n ( u k + 1 − u k ) = ( u 2 − u 1 ) + ( u 3 − u 2 ) + ⋯ + ( u n + 1 − u n ) = u n + 1 − u 1 . \displaystyle s_n=\sum_{k=1}^n\left(u_{k+1}-u_k\right)=\left(u_2-u_1\right)+\left(u_3-u_2\right)+\cdots+\left(u_{n+1}-u_n\right)=u_{n+1}-u_1 . s n = k = 1 ∑ n ( u k + 1 − u k ) = ( u 2 − u 1 ) + ( u 3 − u 2 ) + ⋯ + ( u n + 1 − u n ) = u n + 1 − u 1 . \displaystyle { u n } \left\{u_n\right\} { u n } lim n → ∞ u n + 1 \lim _{n \rightarrow \infty} u_{n+1} lim n → ∞ u n + 1 , , , 从而 lim n → ∞ s n \displaystyle \lim _{n \rightarrow \infty} s_n n → ∞ lim s n ∑ n = 1 ∞ ( u n + 1 − u n ) \sum_{n=1}^{\infty}\left(u_{n+1}-u_n\right) ∑ n = 1 ∞ ( u n + 1 − u n ) 直接法:因为 { u n } \left\{u_n\right\} { u n } lim n → ∞ u n \displaystyle \lim _{n \rightarrow \infty} u_n n → ∞ lim u n a a a 设 ∑ n = 1 ∞ ( u n + 1 2 − u n 2 ) \displaystyle \sum_{n=1}^{\infty}\left(u_{n+1}^2-u_n^2\right) n = 1 ∑ ∞ ( u n + 1 2 − u n 2 ) n n n S n S_n S n S n = u 2 2 − u 1 2 + ⋯ + u n + 1 2 − u n 2 = u n + 1 2 − u 1 2 S_n=u_2^2-u_1^2+\cdots+u_{n+1}^2-u_n^2=u_{n+1}^2-u_1^2 S n = u 2 2 − u 1 2 + ⋯ + u n + 1 2 − u n 2 = u n + 1 2 − u 1 2 lim n → ∞ S n = lim n → ∞ ( u n + 1 2 − u 1 2 ) = a 2 − u 1 2 \displaystyle \lim _{n \rightarrow \infty} S_n=\lim _{n \rightarrow \infty}\left(u_{n+1}^2-u_1^2\right)=a^2-u_1^2 n → ∞ lim S n = n → ∞ lim ( u n + 1 2 − u 1 2 ) = a 2 − u 1 2 (4) 设函数 Q ( x , y ) = x y 2 Q(x, y)=\frac{x}{y^{2}} Q ( x , y ) = y 2 x ( y > 0 ) (y>0) ( y > 0 ) C C C ∮ C P ( x , y ) d x + Q ( x , y ) d y = 0 \oint_{C} P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y=0 ∮ C P ( x , y ) d x + Q ( x , y ) d y = 0 P ( x , y ) P(x, y) P ( x , y ) ( ) (\quad) ( ) y − x 2 y 3 y-\frac{x^{2}}{y^{3}} y − y 3 x 2 1 y − x 2 y 3 \frac{1}{y}-\frac{x^{2}}{y^{3}} y 1 − y 3 x 2 1 x − 1 y \frac{1}{x}-\frac{1}{y} x 1 − y 1 x − 1 y x-\frac{1}{y} x − y 1
(4) 答 应选 D. 解 本题考察曲线积分与路径无关的四个等价命题 ∂ P ∂ y = ∂ Q ∂ x \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} ∂ y ∂ P = ∂ x ∂ Q 已知函数 Q ( x , y ) = x y 2 Q(x, y)=\frac{x}{y^{2}} Q ( x , y ) = y 2 x ∂ Q ∂ x = 1 y 2 \frac{\partial Q}{\partial x}=\frac{1}{y^2} ∂ x ∂ Q = y 2 1 故 ∂ P ∂ y = 1 y 2 \frac{\partial P}{\partial y}=\frac{1}{y^2} ∂ y ∂ P = y 2 1 ∂ P ∂ y = 1 y 2 \frac{\partial P}{\partial y}=\frac{1}{y^2} ∂ y ∂ P = y 2 1 (5) 设 A \boldsymbol{A} A E \boldsymbol{E} E A 2 + A = 2 E \boldsymbol{A}^{2}+\boldsymbol{A}=2 \boldsymbol{E} A 2 + A = 2 E ∣ A ∣ = 4 |\boldsymbol{A}|=4 ∣ A ∣ = 4 x T A x \boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x} x T A x ( ) (\quad) ( ) y 1 2 + y 2 2 + y 3 2 y_{1}^{2}+y_{2}^{2}+y_{3}^{2} y 1 2 + y 2 2 + y 3 2 y 1 2 + y 2 2 − y 3 2 y_{1}^{2}+y_{2}^{2}-y_{3}^{2} y 1 2 + y 2 2 − y 3 2 y 1 2 − y 2 2 − y 3 2 y_{1}^{2}-y_{2}^{2}-y_{3}^{2} y 1 2 − y 2 2 − y 3 2 − y 1 2 − y 2 2 − y 3 2 -y_{1}^{2}-y_{2}^{2}-y_{3}^{2} − y 1 2 − y 2 2 − y 3 2
(5) 设 A \boldsymbol{A} A λ \lambda λ A 2 + A = 2 E \boldsymbol{A}^2+\boldsymbol{A}=2 \boldsymbol{E} A 2 + A = 2 E A 2 + A − 2 E = 0 → 左右两边同乘 α ( A 2 + A − 2 E ) α = 0 \displaystyle A^2 + A - 2E = 0 \xrightarrow[]{\text{左右两边同乘}\alpha} (A^2 + A - 2E)\alpha = 0 A 2 + A − 2 E = 0 左右两边同乘 α ( A 2 + A − 2 E ) α = 0 → E 变 a A 2 α + A α − 2 α = 0 \displaystyle \xrightarrow[]{E\text{变}a} A^2\alpha + A\alpha - 2\alpha = 0 E 变 a A 2 α + A α − 2 α = 0 → A 2 α = λ 2 α A α = λ α λ 2 α + λ α − 2 α = 0 → ( λ 2 + λ − 2 ) α = 0 \displaystyle \xrightarrow[A^2 \alpha=\lambda^2 \alpha]{A \alpha=\lambda \alpha}\lambda^2\alpha + \lambda\alpha - 2\alpha = 0 \rightarrow (\lambda^2 + \lambda - 2)\alpha = 0 A α = λ α A 2 α = λ 2 α λ 2 α + λ α − 2 α = 0 → ( λ 2 + λ − 2 ) α = 0 λ 2 + λ − 2 = 0 → 因式分解 λ = 1 \displaystyle \lambda^2 + \lambda - 2 = 0 \xrightarrow[]{\text{因式分解}} \lambda = 1 \quad λ 2 + λ − 2 = 0 因式分解 λ = 1 − 2 \quad -2 − 2 再由 ∣ A ∣ = 4 |\boldsymbol{A}|=4 ∣ A ∣ = 4 λ ( A ) = − 2 , − 2 , 1 \displaystyle \lambda(A) = -2, -2, 1 λ ( A ) = − 2 , − 2 , 1 所以规范形为 y 1 2 − y 2 2 − y 3 2 y_1^2-y_2^2-y_3^2 y 1 2 − y 2 2 − y 3 2 (6) 如图所示, 有 3 张平面两两相交, 交线相互平行, 它们的方程a i 1 x + a i 2 y + a i 3 z = d i ( i = 1 , 2 , 3 ) a_{i 1} x+a_{i 2} y+a_{i 3} z=d_{i}(i=1,2,3) a i 1 x + a i 2 y + a i 3 z = d i ( i = 1 , 2 , 3 ) A , A ˉ \boldsymbol{A}, \bar{A} A , A ˉ r ( A ) = 2 , r ( A ‾ ) = 3 r(\boldsymbol{A})=2, r(\overline{\boldsymbol{A}})=3 r ( A ) = 2 , r ( A ) = 3 r ( A ) = 2 , r ( A ‾ ) = 2 r(\boldsymbol{A})=2, r(\overline{\boldsymbol{A}})=2 r ( A ) = 2 , r ( A ) = 2 r ( A ) = 1 , r ( A ‾ ) = 2 r(\boldsymbol{A})=1, r(\overline{\boldsymbol{A}})=2 r ( A ) = 1 , r ( A ) = 2 r ( A ) = 1 , r ( A ‾ ) = 1 r(\boldsymbol{A})=1, r(\overline{\boldsymbol{A}})=1 r ( A ) = 1 , r ( A ) = 1
(6) 答 应选 A. 解 由题设知, 三个平面无公共交点, 故方程组无解, 则 r ( A ) ≠ r ( A ‾ ) \mathrm{r}(\boldsymbol{A}) \neq r(\overline{\boldsymbol{A}}) r ( A ) = r ( A ) r ( A ) ⩾ 2 r(\boldsymbol{A}) \geqslant 2 r ( A ) ⩾ 2 表 (a) 方程组有解的情形 图形 几何意义 代数表达 1 三张平面相交于一点 r ( A ) = r ( A ˉ ) = 3 r(A) = r(\bar{A}) = 3 r ( A ) = r ( A ˉ ) = 3 2 三张平面相交于一条直线 r ( A ) = r ( A ˉ ) = 2 r(A) = r(\bar{A}) = 2 r ( A ) = r ( A ˉ ) = 2 β 1 , β 2 , β 3 \beta_1, \beta_2, \beta_3 β 1 , β 2 , β 3 3 两张平面重合,第三张平面与之相交 r ( A ) = r ( A ˉ ) = 2 r(A) = r(\bar{A}) = 2 r ( A ) = r ( A ˉ ) = 2 β 1 , β 2 , β 3 \beta_1, \beta_2, \beta_3 β 1 , β 2 , β 3 4 三张平面重合 r ( A ) = r ( A ˉ ) = 1 r(A) = r(\bar{A}) = 1 r ( A ) = r ( A ˉ ) = 1
图形 几何意义 代数表达 5 三张平面两两相交,且交线相互平行 r ( A ) = 2 , r ( A ˉ ) = 3 r(A) = 2, r(\bar{A}) = 3 r ( A ) = 2 , r ( A ˉ ) = 3 a 1 , a 2 , a 3 a_1, a_2, a_3 a 1 , a 2 , a 3 6 两张平面平行,第三张平面与它们相交 r ( A ) = 2 , r ( A ˉ ) = 3 r(A) = 2, r(\bar{A}) = 3 r ( A ) = 2 , r ( A ˉ ) = 3 a 1 , a 2 , a 3 a_1, a_2, a_3 a 1 , a 2 , a 3
(7) 设 A , B A, B A , B P ( A ) = P ( B ) P(A)=P(B) P ( A ) = P ( B ) ( ) (\quad) ( ) P ( A ∪ B ) = P ( A ) + P ( B ) P(A \cup B)=P(A)+P(B) P ( A ∪ B ) = P ( A ) + P ( B ) P ( A B ) = P ( A ) P ( B ) P(A B)=P(A) P(B) P ( A B ) = P ( A ) P ( B ) P ( A B ˉ ) = P ( B A ˉ ) P(A \bar{B})=P(B \bar{A}) P ( A B ˉ ) = P ( B A ˉ ) P ( A B ) = P ( A ˉ B ˉ ) P(A B)=P(\bar{A} \bar{B}) P ( A B ) = P ( A ˉ B ˉ )
(7) 答 应选 C \mathrm{C} C 对A,B,C,D每个式子都化简 (A) P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) = P ( A ) + P ( B ) \displaystyle P(A \cup B)= P(A)+P(B)-P(A B) =P(A)+P(B) P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) = P ( A ) + P ( B ) P ( A B ) = 0 \displaystyle P(A B) =0 P ( A B ) = 0 (C)可以推出 A A A B B B P ( A B ˉ ) = P ( A − B ) = P ( A ) − P ( A B ) \displaystyle P(A \bar{B})=P(A-B)=P(A)-P(A B) P ( A B ˉ ) = P ( A − B ) = P ( A ) − P ( A B ) P ( B A ˉ ) = P ( B − A ) = P ( B ) − P ( A B ) \displaystyle P(B \bar{A})=P(B-A)=P(B)-P(A B) P ( B A ˉ ) = P ( B − A ) = P ( B ) − P ( A B ) ⇒ P ( A ) = P ( B ) \displaystyle \Rightarrow P(A)=P(B) ⇒ P ( A ) = P ( B ) (D)P ( A B ) = P ( A ˉ B ˉ ) P(A B)=P(\bar{A} \bar{B}) P ( A B ) = P ( A ˉ B ˉ ) P ( A ˉ B ˉ ) = P ( A ˉ ∩ B ˉ ) = 对偶率 P ( A ∪ B ‾ ) = 1 − P ( A ∪ B ) \displaystyle P(\bar{A} \bar{B}) =P(\bar{A} \cap \bar{B})\xlongequal[]{\text{对偶率}}P(\overline{A \cup B})=1-P(A \cup B) P ( A ˉ B ˉ ) = P ( A ˉ ∩ B ˉ ) 对偶率 P ( A ∪ B ) = 1 − P ( A ∪ B ) = 1 − P ( A ) − P ( B ) + P ( A B ) \displaystyle =1-P(A)-P(B)+P(A B) = 1 − P ( A ) − P ( B ) + P ( A B ) P ( A ) + P ( B ) = 1 \displaystyle P(A)+P(B)=1 P ( A ) + P ( B ) = 1 (8) 设随机变量 X X X Y Y Y N ( μ , σ 2 ) \displaystyle N\left(\mu, \sigma^{2}\right) N ( μ , σ 2 ) P { ∣ X − Y ∣ < 1 } ( ) P\{|X-Y|<1\}(\quad) P { ∣ X − Y ∣ < 1 } ( ) μ \mu μ σ 2 \displaystyle \sigma^{2} σ 2 μ \mu μ σ 2 \displaystyle \sigma^{2} σ 2 μ , σ 2 \displaystyle \mu, \sigma^{2} μ , σ 2 μ , σ 2 \displaystyle \mu, \sigma^{2} μ , σ 2
(8) 计算 P { ∣ X − Y ∣ < 1 } P\{|X-Y|<1\} P { ∣ X − Y ∣ < 1 } 观察 X X X Y Y Y X ∼ N ( μ , σ 2 ) \displaystyle X \sim N(\mu, \sigma^2) X ∼ N ( μ , σ 2 ) Y ∼ N ( μ , σ 2 ) \displaystyle Y \sim N(\mu, \sigma^2) Y ∼ N ( μ , σ 2 ) 分析 X − Y X - Y X − Y 则X − Y X - Y X − Y N ( 0 , 2 σ 2 ) \displaystyle N(0, 2\sigma^2) N ( 0 , 2 σ 2 ) → 标准化 X − Y − 0 2 σ ∼ N ( 0 , 1 ) \displaystyle \xrightarrow[]{\text{标准化}}\frac{X-Y-0}{\sqrt{2}\sigma} \sim N(0, 1) 标准化 2 σ X − Y − 0 ∼ N ( 0 , 1 ) 碰到非标准的正态分布习惯上将它转为标准正态 概率也转换为标准正态概率 P { ∣ X − Y ∣ < 1 } = 标准化 X − Y − μ 2 σ P { ∣ X − Y 2 σ ∣ < 1 2 σ } = 正态分布图 2 Φ ( 1 2 σ ) − 1 \displaystyle P\{|X-Y|<1\} \xlongequal[\text{标准化}]{\frac{X-Y-\mu}{\sqrt{2} \sigma}} P\left\{\left|\frac{X-Y}{\sqrt{2} \sigma}\right|<\frac{1}{\sqrt{2} \sigma}\right\}\xlongequal[]{\text{正态分布图}} 2\Phi\left(\frac{1}{\sqrt{2} \sigma}\right) - 1 P { ∣ X − Y ∣ < 1 } 2 σ X − Y − μ 标准化 P { 2 σ X − Y < 2 σ 1 } 正态分布图 2Φ ( 2 σ 1 ) − 1 分析概率值与参数的关系 与 μ \mu μ μ \mu μ 与 σ 2 \displaystyle \sigma^2 σ 2 σ 2 \displaystyle \sigma^2 σ 2 结论:选项 (A) 正确 二、填空题 (本题共 6 小题,每小题 4 分, 共 24 分, 把答案填在题中横线上. )
(9) 设函数 f ( u ) f(u) f ( u ) z = f ( sin y − sin x ) + x y z=f(\sin y-\sin x)+x y z = f ( sin y − sin x ) + x y 1 cos x ⋅ ∂ z ∂ x + 1 cos y ⋅ ∂ z ∂ y = \frac{1}{\cos x} \cdot \frac{\partial z}{\partial x}+\frac{1}{\cos y} \cdot \frac{\partial z}{\partial y}= c o s x 1 ⋅ ∂ x ∂ z + c o s y 1 ⋅ ∂ y ∂ z =
(9) 该问题涉及求函数 z = f ( sin y − sin x ) + x y z=f(\sin y - \sin x) + xy z = f ( sin y − sin x ) + x y 不是具体点,不能先带后求 z / f (siny - sinx) + xy / \ x y 使用链式法则对复合函数求导:求函数 z = f ( sin y − sin x ) + x y z=f(\sin y - \sin x) + xy z = f ( sin y − sin x ) + x y ∂ z ∂ x = f ′ ( sin y − sin x ) ( − cos x ) + y \displaystyle \frac{\partial z}{\partial x} = f'(\sin y - \sin x)(-\cos x) + y ∂ x ∂ z = f ′ ( sin y − sin x ) ( − cos x ) + y ∂ z ∂ y = f ′ ( sin y − sin x ) cos y + x \displaystyle \frac{\partial z}{\partial y} = f'(\sin y - \sin x)\cos y + x ∂ y ∂ z = f ′ ( sin y − sin x ) cos y + x 将∂ z ∂ x \displaystyle \frac{\partial z}{\partial x} ∂ x ∂ z ∂ z ∂ y \frac{\partial z}{\partial y} ∂ y ∂ z 1 cos x ⋅ ∂ z ∂ x + 1 cos y ⋅ ∂ z ∂ y = \displaystyle \frac{1}{\cos x} \cdot \frac{\partial z}{\partial x}+\frac{1}{\cos y} \cdot \frac{\partial z}{\partial y}= cos x 1 ⋅ ∂ x ∂ z + cos y 1 ⋅ ∂ y ∂ z = = 1 cos x ( − f ′ ( sin y − sin x ) cos x + y ) + 1 cos y ( f ′ ( sin y − sin x ) cos y + x ) \displaystyle = \frac{1}{\cos x}(-f'(\sin y - \sin x)\cos x + y) + \frac{1}{\cos y}(f'(\sin y - \sin x)\cos y + x) = cos x 1 ( − f ′ ( sin y − sin x ) cos x + y ) + cos y 1 ( f ′ ( sin y − sin x ) cos y + x ) → 乘进去 1 cos x z x + 1 cos y z y = − f ′ + y cos x + f ′ + x cos y \displaystyle \xrightarrow[]{\text{乘进去}}\frac{1}{\cos x} z_x+\frac{1}{\cos y} z_y=-f^{\prime}+\frac{y}{\cos x}+f^{\prime}+\frac{x}{\cos y} 乘进去 cos x 1 z x + cos y 1 z y = − f ′ + cos x y + f ′ + cos y x = y cos x + x cos y \displaystyle =\frac{y}{\cos x}+\frac{x}{\cos y} = cos x y + cos y x (10) 微分方程 2 y y ′ − y 2 − 2 = 0 2 y y^{\prime}-y^{2}-2=0 2 y y ′ − y 2 − 2 = 0 y ( 0 ) = 1 y(0)=1 y ( 0 ) = 1 y = y= y =
(10) 答 应填 3 e x − 2 \sqrt{3 \mathrm{e}^x-2} 3 e x − 2 原式2 y y ′ − y 2 − 2 = 0 2 y y^{\prime}-y^{2}-2=0 2 y y ′ − y 2 − 2 = 0 2 y ⋅ d y d x = y 2 + 2 \displaystyle 2y \cdot \frac{dy}{dx} = y^2 + 2 2 y ⋅ d x d y = y 2 + 2 → 并两边积分 分离变量 ∫ 2 y y 2 + 2 d y = ∫ d x \displaystyle \xrightarrow[\text{并两边积分}]{\text{分离变量}} \int \frac{2y}{y^2 + 2} dy = \int dx 分离变量 并两边积分 ∫ y 2 + 2 2 y d y = ∫ d x → ∫ 2 y y 2 + 2 d y = ln ( y 2 + 2 ) ln ( y 2 + 2 ) = x + C \displaystyle \xrightarrow[]{\int \frac{2 y}{y^2+2} d y=\ln \left(y^2+2\right)} \ln(y^2 + 2) = x + C ∫ y 2 + 2 2 y d y = l n ( y 2 + 2 ) ln ( y 2 + 2 ) = x + C 代入初值条件: y ( 0 ) = 1 \displaystyle y(0) = 1 y ( 0 ) = 1 ln 3 = C \displaystyle \ln 3 = C ln 3 = C 原式为ln ( y 2 + 2 ) = x + ln 3 \displaystyle \ln(y^2 + 2) = x + \ln 3 ln ( y 2 + 2 ) = x + ln 3 y = \displaystyle y= y = → 加 e e ln ( y 2 + 2 ) = e x + ln 3 \displaystyle \xrightarrow[]{\text{加}e}e^{\ln \left(y^2+2\right)}=e^{x+\ln 3} 加 e e l n ( y 2 + 2 ) = e x + l n 3 → 整理 y 2 + 2 = 3 e x \displaystyle \xrightarrow[]{\text{整理}} y^2 + 2 = 3e^x 整理 y 2 + 2 = 3 e x y 2 = 3 e x − 2 → 开根号 y = ± 3 e x − 2 \displaystyle y^2 = 3e^x - 2 \xrightarrow[]{\text{开根号}} \quad y = \pm\sqrt{3e^x - 2} y 2 = 3 e x − 2 开根号 y = ± 3 e x − 2 因为y ( 0 ) = 1 \displaystyle y(0)=1 y ( 0 ) = 1 y = 3 e x − 2 \displaystyle y = \sqrt{3e^x - 2} y = 3 e x − 2 (11) 幂级数 ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! x n \displaystyle \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n) !} x^{n} n = 0 ∑ ∞ ( 2 n )! ( − 1 ) n x n ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ ) S ( x ) = S(x)= S ( x ) =
(11) cos x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ + ( − 1 ) n x 2 n ( 2 n ) ! + ⋯ , − ∞ < x < + ∞ . \displaystyle \cos x=\sum_{n=0}^{\infty}(-1)^n \frac{x^{2 n}}{(2 n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots+(-1)^n \frac{x^{2 n}}{(2 n)!}+\cdots,-\infty<x<+\infty . cos x = n = 0 ∑ ∞ ( − 1 ) n ( 2 n )! x 2 n = 1 − 2 ! x 2 + 4 ! x 4 − 6 ! x 6 + ⋯ + ( − 1 ) n ( 2 n )! x 2 n + ⋯ , − ∞ < x < + ∞. 已知 cos x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! ( ∣ x ∣ < + ∞ ) \displaystyle \cos x=\sum_{n=0}^{\infty} \frac{(-1)^n x^{2 n}}{(2 n) !}(|x|<+\infty) cos x = n = 0 ∑ ∞ ( 2 n )! ( − 1 ) n x 2 n ( ∣ x ∣ < + ∞ ) 所以∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! x n = 配 ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! ( x ) 2 n = 转 cos x ( 0 < x < + ∞ ) . \displaystyle \sum_{n=0}^{\infty} \frac{(-1)^n}{(2 n) !} x^n\xlongequal[]{\text{配}}\sum_{n=0}^{\infty} \frac{(-1)^n}{(2 n) !}(\sqrt{x})^{2 n}\xlongequal[]{\text{转}}\cos \sqrt{x}(0<x<+\infty) . n = 0 ∑ ∞ ( 2 n )! ( − 1 ) n x n 配 n = 0 ∑ ∞ ( 2 n )! ( − 1 ) n ( x ) 2 n 转 cos x ( 0 < x < + ∞ ) . 方法2 S ( x ) = 1 − x 2 ! + x 2 4 ! − x 3 6 ! + x 4 8 ! − \displaystyle S(x)=1-\frac{x}{2!}+\frac{x^2}{4!}-\frac{x^3}{6!}+\frac{x^4}{8!}- S ( x ) = 1 − 2 ! x + 4 ! x 2 − 6 ! x 3 + 8 ! x 4 − cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ \displaystyle \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots cos x = 1 − 2 ! x 2 + 4 ! x 4 − 6 ! x 6 + ⋯ 令x = t \displaystyle x=\sqrt{t} x = t cos t = 1 − t 2 ! + t 2 4 ! − t 3 6 ! + ⋯ \displaystyle \cos \sqrt{t}=1-\frac{t}{2!}+\frac{t^2}{4!}-\frac{t^3}{6!}+\cdots cos t = 1 − 2 ! t + 4 ! t 2 − 6 ! t 3 + ⋯ 答 应填 cos x \cos \sqrt{x} cos x (12) 设 Σ \displaystyle \Sigma Σ x 2 + y 2 + 4 z 2 = 4 ( z ⩾ 0 ) x^{2}+y^{2}+4 z^{2}=4(z \geqslant 0) x 2 + y 2 + 4 z 2 = 4 ( z ⩾ 0 ) ∬ Σ 4 − x 2 − 4 z 2 d x d y = \displaystyle \iint_{\Sigma} \sqrt{4-x^{2}-4 z^{2}} \mathrm{~d} x \mathrm{~d} y= ∬ Σ 4 − x 2 − 4 z 2 d x d y =
(12) 32 3 \frac{32}{3} 3 32 原曲面是个椭球体:x 2 4 + y 2 4 + z 2 = 1 \displaystyle \frac{x^2}{4} + \frac{y^2}{4} + z^2 = 1 4 x 2 + 4 y 2 + z 2 = 1 本题就是转换投影后的一个平面∬ Σ P d y d z + Q d x d z + R d x d y \displaystyle \iint_{\Sigma} P \, dy \, dz + Q \, dx \, dz + R \, dx \, dy ∬ Σ P d y d z + Q d x d z + R d x d y = 投影向量 n ∬ D ( − P z x − Q z y + R ) d x d y \displaystyle \xlongequal[]{\text{投影向量}n}\iint_{D} (-Pz_x - Qz_y + R) \, dx \, dy 投影向量 n ∬ D ( − P z x − Q z y + R ) d x d y \displaystyle ∬ Σ 4 − x 2 − 4 z 2 d x d y = x 2 + y 2 + 4 z 2 = 4 ∬ Σ y 2 d x d y = ∬ ∣ y ∣ d x d y \iint_{\Sigma} \sqrt{4-x^2-4 z^2} \mathrm{~d} x \mathrm{~d} y\xlongequal[]{x^{2}+y^{2}+4 z^{2}=4}\iint_{\Sigma} \sqrt{y^2} \, dx \, dy = \iint |y| \, dx \, dy ∬ Σ 4 − x 2 − 4 z 2 d x d y x 2 + y 2 + 4 z 2 = 4 ∬ Σ y 2 d x d y = ∬ ∣ y ∣ d x d y = 4 ∬ D 1 y d x d y = 4 ∫ 0 π 2 d θ ∫ 0 2 r 2 sin θ d r \displaystyle = 4 \iint_{D_1} y \, dx \, dy = 4 \int_{0}^{\frac{\pi}{2}} d\theta \int_{0}^{2} r^2 \sin \theta \, dr = 4 ∬ D 1 y d x d y = 4 ∫ 0 2 π d θ ∫ 0 2 r 2 sin θ d r = 4 ∫ 0 π 2 sin θ d θ ∫ 0 2 r 2 d r = r 3 3 ∣ 0 2 = 8 3 4 ⋅ 1 ⋅ 8 3 = 32 3 \displaystyle = 4 \int_{0}^{\frac{\pi}{2}} \sin \theta \, d\theta \int_{0}^{2} r^2 \, dr \xlongequal[]{\left.\frac{r^3}{3}\right|_0 ^2=\frac{8}{3}} 4 \cdot 1 \cdot \frac{8}{3} = \frac{32}{3} = 4 ∫ 0 2 π sin θ d θ ∫ 0 2 r 2 d r 3 r 3 0 2 = 3 8 4 ⋅ 1 ⋅ 3 8 = 3 32 (13) 设 A = ( α 1 , α 2 , α 3 ) \boldsymbol{A}=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\right) A = ( α 1 , α 2 , α 3 ) α 1 , α 2 \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2} α 1 , α 2 α 3 = − α 1 + 2 α 2 \boldsymbol{\alpha}_{3}=-\boldsymbol{\alpha}_{1}+2 \boldsymbol{\alpha}_{2} α 3 = − α 1 + 2 α 2 A x = 0 A x=0 A x = 0
(13) 答 应填 x = k ( 1 , − 2 , 1 ) T , k ∈ R x=k(1,-2,1)^{\mathbf{T}}, k \in \mathbf{R} x = k ( 1 , − 2 , 1 ) T , k ∈ R 确定解向量的个数 由 α 1 , α 2 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2 α 1 , α 2 r ( A ) ⩾ 2 r(\boldsymbol{A}) \geqslant 2 r ( A ) ⩾ 2 α 3 = − α 1 + 2 α 2 \displaystyle \boldsymbol{\alpha}_3=-\boldsymbol{\alpha}_1+2 \boldsymbol{\alpha}_2 α 3 = − α 1 + 2 α 2 r ( A ) < 3 r(\boldsymbol{A})<3 r ( A ) < 3 因此 r ( A ) = 2 \displaystyle r(A) = 2 r ( A ) = 2 n − r ( A ) = 1 \displaystyle n - r(A) = 1 n − r ( A ) = 1 \displaystyle α 3 = − α 1 + 2 α 2 , \alpha_3 = -\alpha_1 + 2\alpha_2, α 3 = − α 1 + 2 α 2 , α 1 − 2 α 2 + α 3 = 0. \alpha_1 - 2\alpha_2 + \alpha_3 = 0. α 1 − 2 α 2 + α 3 = 0. → 化系数矩阵 ( α 1 , α 2 , α 3 ) ( 1 − 2 1 ) ≠ 0. \displaystyle \xrightarrow[]{\text{化系数矩阵}}(\alpha_1, \alpha_2, \alpha_3) \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} \neq 0. 化系数矩阵 ( α 1 , α 2 , α 3 ) 1 − 2 1 = 0. \displaystyle x = k ( 1 , − 2 , 1 ) T , k ∈ R . x = k(1, -2, 1)^T, k \in \mathbb{R}. x = k ( 1 , − 2 , 1 ) T , k ∈ R . (14) 设随机变量 X X X f ( x ) = { x 2 , 0 < x < 2 , 0 , 其他, \displaystyle f(x)= \begin{cases}\frac{x}{2}, & 0<x<2, \\ 0, & \text { 其他, }\end{cases} f ( x ) = { 2 x , 0 , 0 < x < 2 , 其他 , F ( x ) \displaystyle F(x) F ( x ) X \displaystyle X X E ( X ) E(X) E ( X ) X X X P { F ( X ) > E ( X ) − 1 } = P\{F(X)>E(X)-1\}= P { F ( X ) > E ( X ) − 1 } =
(14) 解 求期望 E ( X ) = ∫ 0 2 x f ( x ) d x = ∫ 0 2 x \displaystyle E(X) = \int_0^2 x f(x) dx = \int_0^2 x E ( X ) = ∫ 0 2 x f ( x ) d x = ∫ 0 2 x x 2 d x = x 3 6 ∣ 0 2 = 4 3 \frac{x}{2} dx \left.=\frac{x^3}{6}\right|_0 ^2= \frac{4}{3} 2 x d x = 6 x 3 0 2 = 3 4 确定分布函数 F ( x ) F(x) F ( x ) F ( x ) = ∫ − ∞ x f ( t ) d t = { 0 , x < 0 x 2 4 , 0 ⩽ x < 2 1 , x ⩾ 2 \displaystyle F(x) = \int_{-\infty}^x f(t) dt= \begin{cases} 0, & x < 0 \\ \frac{x^2}{4}, & 0 \leqslant x < 2 \\ 1, & x \geqslant 2 \end{cases} F ( x ) = ∫ − ∞ x f ( t ) d t = ⎩ ⎨ ⎧ 0 , 4 x 2 , 1 , x < 0 0 ⩽ x < 2 x ⩾ 2 x < 0 , F ( x ) = ∫ − ∞ x f ( t ) d t = 0 \displaystyle x<0, \quad F(x)=\int_{-\infty}^x f(t) d t=0 x < 0 , F ( x ) = ∫ − ∞ x f ( t ) d t = 0 0 ⩽ x < 2 , F ( x ) = ∫ − ∞ x f ( t ) d t = ∫ 0 x t 2 d t = x 2 4 \displaystyle 0 \leqslant x<2, \quad F(x)=\int_{-\infty}^x f(t) d t=\int_0^x \frac{t}{2} d t=\frac{x^2}{4} 0 ⩽ x < 2 , F ( x ) = ∫ − ∞ x f ( t ) d t = ∫ 0 x 2 t d t = 4 x 2 2 ⩽ x . F ( x ) = 1 \displaystyle 2 \leqslant x . \quad F(x)=1 2 ⩽ x . F ( x ) = 1 这里休息:一会求期望是对概率密度积分,不是对分布函数积分 李艳芳版 P { F ( X ) > E ( X ) − 1 } = P { F ( X ) > 1 3 } \displaystyle \begin{aligned} P\{F(X)>E(X)-1\} & =P\left\{F(X)>\frac{1}{3}\right\}\end{aligned} P { F ( X ) > E ( X ) − 1 } = P { F ( X ) > 3 1 } = 拆开 P { X 2 4 > 1 3 , 0 ⩽ X < 2 } + P { X ⩾ 2 } \displaystyle \begin{aligned}\xlongequal[]{\text{拆开}}P\left\{\frac{X^2}{4}>\frac{1}{3}, 0 \leqslant X<2\right\}+P\{X \geqslant 2\}\end{aligned} 拆开 P { 4 X 2 > 3 1 , 0 ⩽ X < 2 } + P { X ⩾ 2 } = P { 2 3 < X < 2 } + ∫ 2 + ∞ f ( x ) d x ⏟ = 0 ,概率密度为 0 = 取反求值 1 − ∫ 0 2 3 x 2 d x + 0 \displaystyle \begin{aligned} =P\left\{\frac{2}{\sqrt{3}}<X<2\right\}+\underbrace{\int_2^{+\infty} f(x) \mathrm{d} x}_{=0\text{,概率密度为}0}\xlongequal[]{\text{取反求值}}1-\int_0^{\frac{2}{\sqrt{3}}} \frac{x}{2} \mathrm{~d} x+0 \end{aligned} = P { 3 2 < X < 2 } + = 0 ,概率密度为 0 ∫ 2 + ∞ f ( x ) d x 取反求值 1 − ∫ 0 3 2 2 x d x + 0 = 1 − x 2 4 ∣ 0 2 3 = 2 3 . \displaystyle \begin{aligned} =1-\left.\frac{x^2}{4}\right|_0 ^{\frac{2}{\sqrt{3}}}=\frac{2}{3} . \end{aligned} = 1 − 4 x 2 0 3 2 = 3 2 . 2025版全概率公式 P { F ( x ) > 1 3 } \displaystyle P\left\{F(x)>\frac{1}{3}\right\} P { F ( x ) > 3 1 } = P { x < 0 } P { F ( x ) > 1 3 ∣ x < 0 } ⏟ = 0 + P { 0 ⩽ x < 2 } P { F ( x ) > 1 3 ∣ 0 ⩽ x < 2 } ⏟ P { 0 ⩽ x < 2 , F ( x ) > 1 3 } P { 0 < x < 2 } + \displaystyle =P\{x<0\} \underbrace{P\left\{\left.F(x)>\frac{1}{3} \right\rvert\, x<0\right\}}_{=0}+P\{0 \leqslant x<2\} \underbrace{P\left\{\left.F(x)>\frac{1}{3} \right\rvert\, 0 \leqslant x<2\right\}}_{\frac{P\left\{0 \leqslant x<2, F(x)>\frac{1}{3}\right\}}{P \{0<x<2\}} }+ = P { x < 0 } = 0 P { F ( x ) > 3 1 x < 0 } + P { 0 ⩽ x < 2 } P { 0 < x < 2 } P { 0 ⩽ x < 2 , F ( x ) > 3 1 } P { F ( x ) > 3 1 0 ⩽ x < 2 } + P { 2 ⩽ x } P { F ( x ) > 1 3 ∣ 2 ⩽ x } ⏟ = 1 \displaystyle P\{2 \leqslant x\} \underbrace{P\left\{\left.F(x)>\frac{1}{3} \right\rvert\, 2 \leqslant x\right\}}_{=1} P { 2 ⩽ x } = 1 P { F ( x ) > 3 1 2 ⩽ x } = 条件概率化简 0 + P { 0 ⩽ x < 2 , F ( x ) > 1 3 } + P { 2 ⩽ x } \displaystyle \xlongequal[]{\text{条件概率化简}}0+P\left\{0 \leqslant x<2, F(x)>\frac{1}{3}\right\}+P\{2 \leqslant x\} 条件概率化简 0 + P { 0 ⩽ x < 2 , F ( x ) > 3 1 } + P { 2 ⩽ x } = 转化 F ( x ) = X 2 4 P { 0 ⩽ x < 2 , x 2 4 > 1 3 } + P { 2 ⩽ x } \displaystyle \xlongequal[]{\text{转化}F(x)=\frac{X^2}{4}}P\left\{0 \leqslant x<2, \frac{x^2}{4}>\frac{1}{3}\right\}+P\{2 \leqslant x\} 转化 F ( x ) = 4 X 2 P { 0 ⩽ x < 2 , 4 x 2 > 3 1 } + P { 2 ⩽ x } = 取交集 P { 2 3 < x < 2 } + P { 2 ⩽ x } → 取交集 P { x > 2 3 } \displaystyle \xlongequal[]{\text{取交集}}P\left\{\frac{2}{\sqrt{3}}<x<2\right\}+P\{2 \leqslant x\}\xrightarrow[]{\text{取交集}}P\left\{x>\frac{2}{\sqrt{3}}\right\} 取交集 P { 3 2 < x < 2 } + P { 2 ⩽ x } 取交集 P { x > 3 2 } 2024版 计算 P { F ( X ) > E ( X ) − 1 } P\{F(X) > E(X) - 1\} P { F ( X ) > E ( X ) − 1 } F ( X ) F(X) F ( X ) E ( X ) E(X) E ( X ) P { F ( X ) > E ( X ) − 1 } = 代入 E X = 3 4 P { F ( X ) > 1 3 } \displaystyle P\{F(X) > E(X) - 1\} \xlongequal[\text{代入}]{EX=\frac34}P\left\{F(X)>\frac{1}{3}\right\} P { F ( X ) > E ( X ) − 1 } EX = 4 3 代入 P { F ( X ) > 3 1 } = 转化 F ( x ) = X 2 4 P { X 2 4 > 1 3 } = 开根号 P { X > 2 3 } \xlongequal[]{\text{转化}F(x)=\frac{X^2}{4}}P\left\{\frac{X^2}{4}>\frac{1}{3}\right\}\xlongequal[]{\text{开根号}}P\left\{X>\frac{2}{\sqrt{3}}\right\} 转化 F ( x ) = 4 X 2 P { 4 X 2 > 3 1 } 开根号 P { X > 3 2 } = 小 x 上限为 2 何处求概率 , 何处求积分 ∫ 2 3 2 x 2 d x = 2 3 \displaystyle \xlongequal[\text{小}x\text{上限为}2]{\text{何处求概率},\text{何处求积分}}\int_{\frac{2}{\sqrt{3}}}^2 \frac{x}{2} dx = \frac{2}{3} 何处求概率 , 何处求积分 小 x 上限为 2 ∫ 3 2 2 2 x d x = 3 2 三、解答题 (本题共 9 小题,共 94 分,解答应写出文字说明、证明过程或演算步骤.)}
(15) (本题满分 10 分)y ( x ) y(x) y ( x ) y ′ + x y = e − x 2 2 y^{\prime}+x y=\mathrm{e}^{-\frac{x^{2}}{2}} y ′ + x y = e − 2 x 2 y ( 0 ) = 0 y(0)=0 y ( 0 ) = 0 y ( x ) y(x) y ( x ) y = y ( x ) y=y(x) y = y ( x )
(15) 通解公式y ( x ) = e − ∫ p ( x ) d x ( ∫ g ( x ) ⋅ e ∫ P ( x ) d x d x + C ) \displaystyle y(x)=e^{-\int p(x) d x}\left(\int g(x) \cdot e^{\int P(x) d x} d x+C\right) y ( x ) = e − ∫ p ( x ) d x ( ∫ g ( x ) ⋅ e ∫ P ( x ) d x d x + C ) 原方程为y ′ + x y = e − x 2 2 y^{\prime}+x y=\mathrm{e}^{-\frac{x^{2}}{2}} y ′ + x y = e − 2 x 2 y = e − ∫ x d x ( ∫ e − x 2 2 ⋅ e ∫ x d x d x + C ) \displaystyle y=e^{-\int x d x}\left(\int e^{-\frac{x^2}{2}} \cdot e^{\int x d x} d x+C\right) y = e − ∫ x d x ( ∫ e − 2 x 2 ⋅ e ∫ x d x d x + C ) = e − x 2 2 ( ∫ e − x 2 2 ⋅ e x 2 2 d x + C ) \displaystyle =e^{-\frac{x^2}{2}}\left(\int e^{-\frac{x^2}{2}} \cdot e^{\frac{x^2}{2}} d x+C\right) = e − 2 x 2 ( ∫ e − 2 x 2 ⋅ e 2 x 2 d x + C ) = e − x 2 2 ( ∫ 1 d x + C ) \displaystyle =e^{-\frac{x^2}{2}}\left(\int 1 d x+C\right) = e − 2 x 2 ( ∫ 1 d x + C ) = x e − x 2 2 + C e − x 2 2 \displaystyle =x e^{-\frac{x^2}{2}}+C e^{-\frac{x^2}{2}} = x e − 2 x 2 + C e − 2 x 2 由y ( 0 ) = 0 y(0)=0 y ( 0 ) = 0 0 = C \displaystyle 0=C 0 = C y ( x ) = x e − x 2 2 \displaystyle y(x)=x e^{-\frac{x^2}{2}} y ( x ) = x e − 2 x 2 已知y ( x ) = x e − x 2 2 \displaystyle y(x)=x e^{-\frac{x^2}{2}} y ( x ) = x e − 2 x 2 y ′ = e − x 2 2 + x ⋅ e − x 2 2 ⋅ ( − x ) = ( 1 − x 2 ) e − x 2 2 , \displaystyle y^{\prime}=\mathrm{e}^{-\frac{x^2}{2}}+x \cdot \mathrm{e}^{-\frac{x^2}{2}} \cdot(-x)=\left(1-x^2\right) \mathrm{e}^{-\frac{x^2}{2}}, y ′ = e − 2 x 2 + x ⋅ e − 2 x 2 ⋅ ( − x ) = ( 1 − x 2 ) e − 2 x 2 , y ′ ′ = ( − 2 x ) e − x 2 2 + ( 1 − x 2 ) ⋅ e − x 2 2 ⋅ ( − x ) = ( x 3 − 3 x ) e − x 2 2 \displaystyle y^{\prime \prime}=(-2 x) \mathrm{e}^{-\frac{x^2}{2}}+\left(1-x^2\right) \cdot \mathrm{e}^{-\frac{x^2}{2}} \cdot(-x)=\left(x^3-3 x\right) \mathrm{e}^{-\frac{x^2}{2}} y ′′ = ( − 2 x ) e − 2 x 2 + ( 1 − x 2 ) ⋅ e − 2 x 2 ⋅ ( − x ) = ( x 3 − 3 x ) e − 2 x 2 = x ( x − 3 ) ( x + 3 ) \displaystyle =x(x-\sqrt{3})(x+\sqrt{3}) = x ( x − 3 ) ( x + 3 ) e − x 2 2 e^{-\frac{x^2}{2}} e − 2 x 2 x < − 3 , y ′ ′ < 0 ⇒ ( − ∞ , − 3 ) \displaystyle x<-\sqrt{3}, y^{\prime \prime}<0 \Rightarrow(-\infty,-\sqrt{3}) x < − 3 , y ′′ < 0 ⇒ ( − ∞ , − 3 ) − 3 < x < 0 , y ′ ′ > 0 ⇒ ( − 3 , 0 ) \displaystyle -\sqrt{3}<x<0, y^{\prime \prime}>0 \Rightarrow(-\sqrt{3}, 0) − 3 < x < 0 , y ′′ > 0 ⇒ ( − 3 , 0 ) 0 < x < 3 , y ′ ′ < 0 \displaystyle 0<x<\sqrt{3}, y^{\prime \prime}<0 0 < x < 3 , y ′′ < 0 ( 0 , 3 ) \displaystyle (0, \sqrt{3}) ( 0 , 3 ) x > 3 , y ′ ′ > 0 x>\sqrt{3}, y^{\prime \prime}>0 x > 3 , y ′′ > 0 ( 3 , + ∞ ) \displaystyle (\sqrt{3},+\infty) ( 3 , + ∞ ) 因此 y = y ( x ) y=y(x) y = y ( x ) 凹区间为 ( − 3 , 0 ) (-\sqrt{3}, 0) ( − 3 , 0 ) ( 3 , + ∞ ) (\sqrt{3},+\infty) ( 3 , + ∞ ) 凸区间为 ( − ∞ , − 3 ) (-\infty,-\sqrt{3}) ( − ∞ , − 3 ) ( 0 , 3 ) (0, \sqrt{3}) ( 0 , 3 ) 拐点共有 3 个: ( − 3 , − 3 e − 3 2 ) , ( 0 , 0 ) , ( 3 , 3 e − 3 2 ) \left(-\sqrt{3},-\sqrt{3} \mathrm{e}^{-\frac{3}{2}}\right),(0,0),\left(\sqrt{3}, \sqrt{3} \mathrm{e}^{-\frac{3}{2}}\right) ( − 3 , − 3 e − 2 3 ) , ( 0 , 0 ) , ( 3 , 3 e − 2 3 ) (16) (本题满分 10 分)a , b a, b a , b z = 2 + a x 2 + b y 2 z=2+a x^{2}+b y^{2} z = 2 + a x 2 + b y 2 ( 3 , 4 ) (3,4) ( 3 , 4 ) l = − 3 i − 4 j \boldsymbol{l}=-3 \boldsymbol{i}-4 \boldsymbol{j} l = − 3 i − 4 j a , b a, b a , b z = 2 + a x 2 + b y 2 ( z ⩾ 0 ) z=2+a x^{2}+b y^{2}(z \geqslant 0) z = 2 + a x 2 + b y 2 ( z ⩾ 0 )
(16) (I) 计算函数 z = 2 + a x 2 + b y 2 z=2+a x^2+b y^2 z = 2 + a x 2 + b y 2 ( 3 , 4 ) (3,4) ( 3 , 4 ) grad z ( x , y ) ∣ ( 3 , 4 ) = ( z x ′ , z y ′ ) ∣ ( 3 , 4 ) = ( 2 a x , 2 b y ) ∣ ( 3 , 4 ) = ( 6 a , 8 b ) . \left.\operatorname{grad} z(x, y)\right|_{(3,4)}=\left.\left(z_x^{\prime}, z_y^{\prime}\right)\right|_{(3,4)}=\left.(2 a x, 2 b y)\right|_{(3,4)}=(6 a, 8 b) . grad z ( x , y ) ∣ ( 3 , 4 ) = ( z x ′ , z y ′ ) ( 3 , 4 ) = ( 2 a x , 2 b y ) ∣ ( 3 , 4 ) = ( 6 a , 8 b ) . 由 6 a i + 8 b j 6 a i+8 b j 6 ai + 8 bj − 3 i − 4 j -3 i-4 j − 3 i − 4 j 6 a − 3 = 8 b − 4 > 0 → 化简 a = b < 0 \frac{6 a}{-3}=\frac{8 b}{-4}>0\xrightarrow[]{\text{化简}}a=b<0 − 3 6 a = − 4 8 b > 0 化简 a = b < 0 方向导数最大值为 ( 6 a ) 2 + ( 8 b ) 2 = 10 \sqrt{(6 a)^2+(8 b)^2}=10 ( 6 a ) 2 + ( 8 b ) 2 = 10 ( 6 a ) 2 + ( 8 b ) 2 = 100 a 2 = 100 (6 a)^2+(8 b)^2=100 a^2=100 ( 6 a ) 2 + ( 8 b ) 2 = 100 a 2 = 100 → 整理 a = ± 1 ⇒ a = − 1 = b \displaystyle \xrightarrow[]{\text{整理}} a= \pm 1 \Rightarrow a=-1=b 整理 a = ± 1 ⇒ a = − 1 = b 若积分曲面 Σ \displaystyle \Sigma Σ z = z ( x , y ) z=z(x, y) z = z ( x , y ) Σ \displaystyle \Sigma Σ x O y x O y x O y D x y D_{x y} D x y z = z ( x , y ) z=z(x, y) z = z ( x , y ) D x y D_{x y} D x y f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \displaystyle \Sigma Σ ∬ Σ f ( x , y , z ) d S = ∬ D x y f ( x , y , z ( x , y ) ) 1 + z x ′ 2 ( x , y ) + z y ′ 2 ( x , y ) d x d y . \displaystyle \iint_{\Sigma} f(x, y, z) \mathrm{d} S=\iint_{D_{x y}} f(x, y, z(x, y)) \sqrt{1+z_x^{\prime 2}(x, y)+z_y^{\prime 2}(x, y)} \mathrm{d} x \mathrm{~d} y . ∬ Σ f ( x , y , z ) d S = ∬ D x y f ( x , y , z ( x , y )) 1 + z x ′2 ( x , y ) + z y ′2 ( x , y ) d x d y . ( II) 由第( I) 问可知曲面 Σ \displaystyle \Sigma Σ z = 2 − x 2 − y 2 ( z ⩾ 0 ) z=2-x^2-y^2(z \geqslant 0) z = 2 − x 2 − y 2 ( z ⩾ 0 ) ∬ Σ d S \displaystyle \iint_{\Sigma} \mathrm{d} S ∬ Σ d S z x ′ = − 2 x , z y ′ = − 2 y , d S = 1 + 4 x 2 + 4 y 2 d x d y . z_x^{\prime}=-2 x, z_y^{\prime}=-2 y, \mathrm{~d} S=\sqrt{1+4 x^2+4 y^2} \mathrm{~d} x \mathrm{~d} y . z x ′ = − 2 x , z y ′ = − 2 y , d S = 1 + 4 x 2 + 4 y 2 d x d y . 令 z = 0 z=0 z = 0 Σ \displaystyle \Sigma Σ x O y x O y x O y D x y = { { ( x , y ) ∣ x 2 + y 2 ⩽ 2 } D_{x y}=\left\{\left\{(x, y) \mid x^2+y^2 \leqslant 2\right\}\right. D x y = { { ( x , y ) ∣ x 2 + y 2 ⩽ 2 } S = ∬ Σ d S = ∬ D x y 1 + ( z x ′ ) 2 + ( z y ′ ) 2 d x d y \displaystyle S=\iint_{\Sigma} \mathrm{d} S =\iint_{D_{x y}} \sqrt{1+\left(z_x^{\prime}\right)^2+\left(z_y^{\prime}\right)^2} \mathrm{~d} x \mathrm{~d} y S = ∬ Σ d S = ∬ D x y 1 + ( z x ′ ) 2 + ( z y ′ ) 2 d x d y = ∬ D x y 1 + 4 x 2 + 4 y 2 d x d y \displaystyle =\iint_{D_{x y}} \sqrt{1+4 x^2+4 y^2} \mathrm{~d} x \mathrm{~d} y = ∬ D x y 1 + 4 x 2 + 4 y 2 d x d y = 极坐标 ∫ 0 2 π d θ ∫ 0 2 1 + 4 r 2 ⋅ r d r \displaystyle \xlongequal{\text{ 极坐标 }} \int_0^{2 \pi} \mathrm{~d} \theta \int_0^{\sqrt{2}} \sqrt{1+4 r^2} \cdot r \mathrm{~d} r 极坐标 ∫ 0 2 π d θ ∫ 0 2 1 + 4 r 2 ⋅ r d r = 2 π ⋅ 1 8 ∫ 0 2 1 + 4 r 2 d ( 1 + 4 r 2 ) \displaystyle =2 \pi \cdot \frac{1}{8} \int_0^{\sqrt{2}} \sqrt{1+4 r^2} \mathrm{~d}\left(1+4 r^2\right) = 2 π ⋅ 8 1 ∫ 0 2 1 + 4 r 2 d ( 1 + 4 r 2 ) = π 4 ⋅ 2 3 ( 1 + 4 r 2 ) 3 2 ∣ 0 2 \displaystyle =\left.\frac{\pi}{4} \cdot \frac{2}{3}\left(1+4 r^2\right)^{\frac{3}{2}}\right|_0 ^{\sqrt{2}} = 4 π ⋅ 3 2 ( 1 + 4 r 2 ) 2 3 0 2 = π 4 × 2 3 × ( 27 − 1 ) = 13 π 3 . \displaystyle =\frac{\pi}{4} \times \frac{2}{3} \times(27-1)=\frac{13 \pi}{3} . = 4 π × 3 2 × ( 27 − 1 ) = 3 13 π . 2015 年数一试题f ( x , y ) = x + y + x y f(x, y)=x+y+x y f ( x , y ) = x + y + x y C : x 2 + y 2 + x y = 3 C: x^2+y^2+x y=3 C : x 2 + y 2 + x y = 3 f ( x , y ) f(x, y) f ( x , y ) C C C (17) (本题满分 10 分)y = e − x sin x ( x ⩾ 0 ) y=\mathrm{e}^{-x} \sin x(x \geqslant 0) y = e − x sin x ( x ⩾ 0 ) x x x
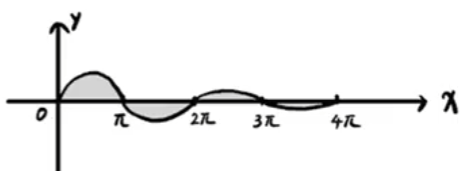
(17) 小崔版 → 加绝对值 算面积 ∫ 0 + ∞ ∣ e − x sin x ∣ d x \displaystyle \xrightarrow[\text{加绝对值}]{\text{算面积}}\int_0^{+\infty}\left|e^{-x} \sin x\right| d x 算面积 加绝对值 ∫ 0 + ∞ e − x sin x d x = ∫ 0 π e − x sin x d x − ∫ π 2 π e − x sin x d x + ∫ 2 π 3 π − ∫ 3 π 4 π + ⋯ \displaystyle = \int_0^\pi e^{-x} \sin x d x-\int_\pi^{2 \pi} e^{-x} \sin x d x+\int_{2 \pi}^{3 \pi}-\int_{3 \pi}^{4 \pi}+\cdots = ∫ 0 π e − x sin x d x − ∫ π 2 π e − x sin x d x + ∫ 2 π 3 π − ∫ 3 π 4 π + ⋯ S = ∑ n = 0 ∞ ( − 1 ) n ∫ n π ( n + 1 ) π e − x sin x d x ‾ → 以暴制暴 ∑ n = 0 ∞ ( − 1 ) n u n \displaystyle S= \sum_{n=0}^{\infty}(-1)^n \underline{\int_{n \pi}^{(n+1) \pi} e^{-x} \sin x d x }\xrightarrow[]{\text{以暴制暴}}\sum_{n=0}^{\infty}(-1)^n u_n S = n = 0 ∑ ∞ ( − 1 ) n ∫ nπ ( n + 1 ) π e − x sin x d x 以暴制暴 n = 0 ∑ ∞ ( − 1 ) n u n ∫ n π ( n + 1 ) π e − x sin x d x = − ∫ n π ( n + 1 ) π sin x d ( e − x ) \displaystyle \int_{n \pi}^{(n+1)\pi} e^{-x} \sin x d x=-\int_{n \pi}^{(n+1) \pi} \sin x d\left(e^{-x}\right) ∫ nπ ( n + 1 ) π e − x sin x d x = − ∫ nπ ( n + 1 ) π sin x d ( e − x ) = 分布 − e − x sin π ∣ n π ( π + 1 ) π ⏟ = 0 − 0 = 0 + ∫ n π ( n + 1 ) π e − x ⋅ cos x d x \displaystyle \xlongequal[]{\text{分布}}\underbrace{-e^{-x} \sin \pi |_{n \pi}^{(\pi+1) \pi}}_{=0-0=0}+\int_{n \pi}^{(n+1) \pi} e^{-x} \cdot \cos x d x 分布 = 0 − 0 = 0 − e − x sin π ∣ nπ ( π + 1 ) π + ∫ nπ ( n + 1 ) π e − x ⋅ cos x d x = − ∫ n π ( n + 1 ) π cos x d ( e − x ) \displaystyle =-\int_{n \pi}^{(n+1) \pi} \cos x d\left(e^{-x}\right) = − ∫ nπ ( n + 1 ) π cos x d ( e − x ) = 分布积分 − e − x cos x ∫ n π ( n + 1 ) π − ∫ n π ( n + 1 ) π e − x sin x d x \displaystyle \xlongequal[]{\text{分布积分}}-e^{-x} \cos x \int_{n \pi}^{(n+1) \pi}-\int_{n \pi}^{(n+1) \pi} e^{-x} \sin x d x 分布积分 − e − x cos x ∫ nπ ( n + 1 ) π − ∫ nπ ( n + 1 ) π e − x sin x d x u n = − e − x cos x ∣ n π ( n + 1 ) π \displaystyle u_n =-\left.e^{-x} \cos x\right|_{n \pi} ^{(n+1) \pi} u n = − e − x cos x nπ ( n + 1 ) π = 1 2 [ e − ( n + 1 ) π ( − 1 ) n + 2 − e − n π ( − 1 ) n + 1 ] \displaystyle =\frac{1}{2}\left[e^{-(n+1) \pi}(-1)^{n+2}-e^{-n \pi}(-1)^{n+1}\right] = 2 1 [ e − ( n + 1 ) π ( − 1 ) n + 2 − e − nπ ( − 1 ) n + 1 ] cos n π = ( − 1 ) n \cos n \pi=(-1)^n cos nπ = ( − 1 ) n − e − ( n + 1 ) π cos ( n + 1 ) π = e − ( n + 1 ) π ⋅ ( − 1 ) n + 2 -e^{-(n+1) \pi} \cos (n+1) \pi=e^{-(n+1) \pi} \cdot(-1)^{n+2} − e − ( n + 1 ) π cos ( n + 1 ) π = e − ( n + 1 ) π ⋅ ( − 1 ) n + 2 − e − n π cos n π = e − n π ( − 1 ) n + 1 -e^{-n \pi} \cos n \pi=e^{-n \pi}(-1)^{n+1} − e − nπ cos nπ = e − nπ ( − 1 ) n + 1 S = ∑ n = 0 ∞ 1 2 [ e − ( n + 1 ) π ( − 1 ) 2 n + 2 − e − n π ( − 1 ) 2 n + 1 ] \displaystyle S =\sum_{n=0}^{\infty} \frac{1}{2}\left[e^{-(n+1) \pi}(-1)^{2 n+2}-e^{-n \pi}(-1)^{2 n+1}\right] S = n = 0 ∑ ∞ 2 1 [ e − ( n + 1 ) π ( − 1 ) 2 n + 2 − e − nπ ( − 1 ) 2 n + 1 ] = ∑ n = 0 ∞ 1 2 ( e − ( n + 1 ) π + e − n π ) \displaystyle =\sum_{n=0}^{\infty} \frac{1}{2}\left(e^{-(n+1) \pi}+e^{-n \pi}\right) = n = 0 ∑ ∞ 2 1 ( e − ( n + 1 ) π + e − nπ ) e − π + e − 0 π , e − 2 π + e − π , e − 3 π + e − 2 π e^{-\pi}+e^{-0 \pi}, e^{-2 \pi}+e^{-\pi}, e^{-3 \pi}+e^{-2 \pi} e − π + e − 0 π , e − 2 π + e − π , e − 3 π + e − 2 π e − π + e − 0 π \displaystyle e^{-\pi}+e^{-0 \pi} e − π + e − 0 π e − π \displaystyle e^{-\pi} e − π 等比数列求和 = 1 减公比分之首项 1 2 e − π + 1 1 − e − π = 1 + e π 2 ( e π − 1 ) . \displaystyle \xlongequal[]{1\text{减公比分之首项}}\frac{1}{2} \frac{e^{-\pi}+1}{1-e^{-\pi}}=\frac{1+e^\pi}{2\left(e^\pi-1\right)} . 1 减公比分之首项 2 1 1 − e − π e − π + 1 = 2 ( e π − 1 ) 1 + e π . 郭伟版 计算面积 S S S 面积 S S S S = ∫ 0 + ∞ e − x ∣ sin x ∣ d x \displaystyle S = \int_0^{+\infty} \mathrm{e}^{-x}|\sin x| \mathrm{d} x S = ∫ 0 + ∞ e − x ∣ sin x ∣ d x 将积分区间分解为无穷多个小区间。 每个小区间的积分计算为 ∫ k π ( k + 1 ) π e − x sin x d x \displaystyle \int_{k \pi}^{(k+1) \pi} \mathrm{e}^{-x} \sin x \mathrm{~d} x ∫ kπ ( k + 1 ) π e − x sin x d x 整个区间的面积S n = ∑ k = 1 n ∫ k π ( k + 1 ) π e − x ∣ sin x ∣ d x = 从 n 到 n − 1 k 从 1 到 0 ∑ k = 0 n − 1 ∫ k π ( k + 1 ) π e − x ∣ sin x ∣ d x \displaystyle S_n=\sum_{k=1}^{n}\int_{k \pi}^{(k+1) \pi} \mathrm{e}^{-x}|\sin x| \mathrm{d} x\xlongequal[\text{从}n\text{到}n-1]{k\text{从}1\text{到}0}\sum_{k=0}^{n-1} \int_{k \pi}^{(k+1) \pi} \mathrm{e}^{-x}|\sin x| \mathrm{d} x S n = k = 1 ∑ n ∫ kπ ( k + 1 ) π e − x ∣ sin x ∣ d x k 从 1 到 0 从 n 到 n − 1 k = 0 ∑ n − 1 ∫ kπ ( k + 1 ) π e − x ∣ sin x ∣ d x 计算每个小区间的积分: ∫ k π ( k + 1 ) π e − x sin x d x = d x = d t x = t + k π ∫ 0 π e − ( t + k π ) ∣ sin ( t + k π ) ∣ d t = 且 sin ( t + k π ) = sin t 提出常数部分 e − k π = e − k π ∫ 0 π e − t sin t d t \displaystyle \int_{k \pi}^{(k+1) \pi} \mathrm{e}^{-x} \sin x \mathrm{~d} x \xlongequal[d x=d t]{x=t+k \pi}\int_0^\pi \mathrm{e}^{-(t+k \pi)}|\sin (t+k \pi)| \mathrm{d} t\xlongequal[\text{且}\sin (t+k \pi)=\sin t]{\text{提出常数部分}e^{-k\pi}}=\mathrm{e}^{-k \pi} \int_0^\pi \mathrm{e}^{-t} \sin t \mathrm{~d} t ∫ kπ ( k + 1 ) π e − x sin x d x x = t + kπ d x = d t ∫ 0 π e − ( t + kπ ) ∣ sin ( t + kπ ) ∣ d t 提出常数部分 e − kπ 且 s i n ( t + kπ ) = s i n t = e − kπ ∫ 0 π e − t sin t d t 其中换积分限:由 t = x − k π t=x-k \pi t = x − kπ { 上限: ( k + 1 ) π − k π = π 下限 : k π − k π = 0 \displaystyle \left\{\begin{array}{l}\text { 上限: }(k+1) \pi-k \pi=\pi \\\text{下限}: k \pi-k \pi=0\end{array}\right. { 上限 : ( k + 1 ) π − kπ = π 下限 : kπ − kπ = 0 转换为:单独计算第二部分:同时出现e和sin,连续分布两次,以暴制暴 第一次分部:( ∫ 0 π e − t sin t d t ) = − ∫ 0 π sin t d ( e − t ) = 分部 − ( sin t e − t ∣ 0 π ⏟ 0 − 0 = 0 − ∫ 0 π e − t cos t d t ) = ∫ 0 π e − t cos t d t \displaystyle \left(\int_0^\pi \mathrm{e}^{-t} \sin t \mathrm{~d} t\right)=-\int_0^\pi \sin t \mathrm{~d}\left(\mathrm{e}^{-t}\right)\xlongequal[]{\text{分部}}-\left(\underbrace{\left.\sin t \mathrm{e}^{-t}\right|_0 ^\pi}_{0-0=0} -\int_0^\pi\mathrm{e}^{-t} \cos t \mathrm{~d} t\right)=\int_0^\pi \mathrm{e}^{-t} \cos t \mathrm{~d} t ( ∫ 0 π e − t sin t d t ) = − ∫ 0 π sin t d ( e − t ) 分部 − 0 − 0 = 0 sin t e − t 0 π − ∫ 0 π e − t cos t d t = ∫ 0 π e − t cos t d t 第二次分布:∫ 0 π e − t cos t d t = = − ∫ 0 π cos t d ( e − t ) = − cos t e − t ∣ 0 π ⏟ e − π + 1 − ∫ 0 π e − t sin t d t = e − π + 1 − ∫ 0 π e − t sin t d t . \displaystyle \int_0^\pi \mathrm{e}^{-t} \cos t \mathrm{~d} t==-\int_0^\pi \cos t \mathrm{~d}\left(\mathrm{e}^{-t}\right)=\underbrace{-\left.\cos t \mathrm{e}^{-t}\right|_0 ^\pi}_{\mathrm{e}^{-\pi}+1}-\int_0^\pi \mathrm{e}^{-t} \sin t \mathrm{~d} t=\mathrm{e}^{-\pi}+1-\int_0^\pi \mathrm{e}^{-t} \sin t \mathrm{~d} t . ∫ 0 π e − t cos t d t == − ∫ 0 π cos t d ( e − t ) = e − π + 1 − cos t e − t 0 π − ∫ 0 π e − t sin t d t = e − π + 1 − ∫ 0 π e − t sin t d t . 整理头尾得:∫ 0 π e − t ⋅ sin t d t = 与第二次分布相等 e − π + 1 − ∫ 0 π e − t sin t d t . \displaystyle \int_0^\pi e^{-t} \cdot \sin t d t\xlongequal[]{\text{与第二次分布相等}}\mathrm{e}^{-\pi}+1-\int_0^\pi \mathrm{e}^{-t} \sin t \mathrm{~d} t . ∫ 0 π e − t ⋅ sin t d t 与第二次分布相等 e − π + 1 − ∫ 0 π e − t sin t d t . 移项得∫ 0 π e − t ⋅ sin t d t = 1 2 ( e − π + 1 ) \displaystyle \int_0^\pi e^{-t} \cdot \sin t d t=\frac{1}{2}\left(e^{-\pi}+1\right) ∫ 0 π e − t ⋅ sin t d t = 2 1 ( e − π + 1 ) 则每段区间的面积为 ∫ k π ( k + 1 ) π e − x ⋅ ∣ sin x ∣ = 1 2 e − k π ⋅ ( e π + 1 ) = 1 2 [ e − k π + e ( − k + 1 ) π ] \displaystyle \int_{k \pi}^{(k+1) \pi} e^{-x} \cdot|\sin x|=\frac{1}{2} e^{-k \pi} \cdot\left(e^\pi+1\right)=\frac{1}{2} [e^{-k \pi}+ e^{(-k+1) \pi}] ∫ kπ ( k + 1 ) π e − x ⋅ ∣ sin x ∣ = 2 1 e − kπ ⋅ ( e π + 1 ) = 2 1 [ e − kπ + e ( − k + 1 ) π ] 使用级数求和公式 S n = 1 2 ∑ k = 0 n − 1 [ e − ( k + 1 ) π + e − k π ] = 拆开,变指数 1 2 [ ∑ k = 1 n − 1 e − ( k + 1 ) π ⏟ ∑ k = 1 n e − ( k ) π + ∑ k = 0 n − 1 e − k π ] \displaystyle S_n=\frac{1}{2} \sum_{k=0}^{n-1}\left[e^{-(k+1) \pi}+e^{-k \pi}\right]\xlongequal[]{\text{拆开,变指数}}\frac{1}{2}\left[\underbrace{\sum_{k=1}^{n-1} e^{-(k+1) \pi}}_{\sum_{k=1}^{n} e^{-(k) \pi}}+\sum_{k=0}^{n-1} e^{-k \pi}\right] S n = 2 1 k = 0 ∑ n − 1 [ e − ( k + 1 ) π + e − kπ ] 拆开,变指数 2 1 ∑ k = 1 n e − ( k ) π k = 1 ∑ n − 1 e − ( k + 1 ) π + k = 0 ∑ n − 1 e − kπ 级数配平 配∑ k = 1 n e − ( k ) π = \displaystyle \sum_{k=1}^{n} e^{-(k) \pi}= k = 1 ∑ n e − ( k ) π = 配∑ k = 0 n − 1 e − k π = − e 0 + e 0 k 下限从 0 到 1 ∑ k = 1 n − 1 e − k π + 1 = 先加 e − n π 再减去 k 上限从 n − 1 到 n ∑ k = 1 n e − ( k ) π + 1 − e − n π \displaystyle \sum_{k=0}^{n-1} e^{-k \pi}\xlongequal[-e^0+e^0]{k\text{下限从}0\text{到}1}\sum_{k=1}^{n-1} e^{-k \pi}+1\xlongequal[\text{先加}e^{-n\pi}\text{再减去}]{k\text{上限从}n-1\text{到}n}\sum_{k=1}^{n} e^{-(k) \pi}+1-e^{-n\pi} k = 0 ∑ n − 1 e − kπ k 下限从 0 到 1 − e 0 + e 0 k = 1 ∑ n − 1 e − kπ + 1 k 上限从 n − 1 到 n 先加 e − nπ 再减去 k = 1 ∑ n e − ( k ) π + 1 − e − nπ 合并配平项,得= 1 2 ⋅ [ 2 ∑ k = 1 n e − k π + 1 − e − n π ] = 计算等比求和 1 2 ⋅ [ 1 − e − n π e π − 1 + 1 − e − n π ] \displaystyle =\frac{1}{2} \cdot\left[2 \sum_{k=1}^n e^{-k \pi}+1-e^{-n \pi}\right]\xlongequal[]{\text{计算等比求和}}\frac{1}{2} \cdot\left[\frac{1-e^{-n \pi}}{e^\pi-1}+1-e^{-n \pi}\right] = 2 1 ⋅ [ 2 k = 1 ∑ n e − kπ + 1 − e − nπ ] 计算等比求和 2 1 ⋅ [ e π − 1 1 − e − nπ + 1 − e − nπ ] 等比求和:∑ k = 1 n e − k π = a 1 ( 1 − q n ) 1 − q e − π ⋅ ( 1 − e − n π ) 1 − e − π = 同乘 e π 1 − e − n π e π − 1 \displaystyle \sum_{k=1}^n e^{-k \pi}\xlongequal[]{\frac{a_1\left(1-q^n\right)}{1-q}}\frac{e^{-\pi} \cdot\left(1-e^{-n \pi}\right)}{1-e^{-\pi}}\xlongequal[]{\text{同乘}e^{\pi}}\frac{1-e^{-n \pi}}{e^\pi-1} k = 1 ∑ n e − kπ 1 − q a 1 ( 1 − q n ) 1 − e − π e − π ⋅ ( 1 − e − nπ ) 同乘 e π e π − 1 1 − e − nπ 求极限lim n → ∞ S n \displaystyle \lim _{n \rightarrow \infty} S_n n → ∞ lim S n lim n → ∞ S n = lim n → ∞ 1 2 ⋅ [ 1 − e − n π e π − 1 + 1 − e − n π ] = lim n → ∞ e − n π = 0 1 2 + 1 e 2 − 1 \displaystyle \lim _{n \rightarrow \infty} S_n=\lim _{n \rightarrow \infty} \frac{1}{2} \cdot\left[\frac{1-e^{-n \pi}}{e^\pi-1}+1-e^{-n \pi}\right]\xlongequal[]{\lim _{n \rightarrow \infty} e^{-n \pi}=0}\frac{1}{2}+\frac{1}{e^2-1} n → ∞ lim S n = n → ∞ lim 2 1 ⋅ [ e π − 1 1 − e − nπ + 1 − e − nπ ] l i m n → ∞ e − nπ = 0 2 1 + e 2 − 1 1 (18) (本题满分 10 分)a n = ∫ 0 1 x n 1 − x 2 d x ( n = 0 , 1 , 2 , ⋯ ) \displaystyle a_{n}=\int_{0}^{1} x^{n} \sqrt{1-x^{2}} \mathrm{~d} x(n=0,1,2, \cdots) a n = ∫ 0 1 x n 1 − x 2 d x ( n = 0 , 1 , 2 , ⋯ ) { a n } \left\{a_{n}\right\} { a n } a n = n − 1 n + 2 a n − 2 ( n = 2 , 3 , ⋯ ) a_{n}=\frac{n-1}{n+2} a_{n-2}(n=2,3, \cdots) a n = n + 2 n − 1 a n − 2 ( n = 2 , 3 , ⋯ ) lim n → ∞ a n a n − 1 \displaystyle \lim _{n \rightarrow \infty} \frac{a_{n}}{a_{n-1}} n → ∞ lim a n − 1 a n
(18) 证明数列 { a n } \left\{a_{n}\right\} { a n } a n + 1 = ∫ 0 1 x n + 1 1 − x 2 d x \displaystyle \begin{aligned} & a_{n+1}=\int_0^1 x^{n+1} \sqrt{1-x^2} d x \end{aligned} a n + 1 = ∫ 0 1 x n + 1 1 − x 2 d x a n = ∫ 0 1 x n 1 − x 2 d x \displaystyle \begin{aligned} a_n=\int_0^1 x^n \sqrt{1-x^2} d x \end{aligned} a n = ∫ 0 1 x n 1 − x 2 d x a n + 1 − a n = ∫ 0 1 ( x n + 1 − x n ) ⏟ 小减大 = 负数 1 − x 2 d x < 0 \displaystyle \begin{aligned} a_{n+1}-a_n=\int_0^1 \underbrace{(x^{n+1}-x^n)}_{\text{小减大}=\text{负数}}\sqrt{1-x^2} d x<0 \end{aligned} a n + 1 − a n = ∫ 0 1 小减大 = 负数 ( x n + 1 − x n ) 1 − x 2 d x < 0 a n + 1 < a n a n ↘ \displaystyle \begin{aligned} a_{n+1}<a_n \quad a_n \searrow \end{aligned} a n + 1 < a n a n ↘ a n = ∫ 0 1 x n 1 − x 2 d x = 根号看着不顺眼 x = sin t ∫ 0 π 2 sin n t ⋅ cos 2 t d t → cos 2 t = ( 1 − sin 2 t ) \displaystyle \begin{aligned} a_n & =\int_0^1 x^n \sqrt{1-x^2} d x \xlongequal[\text{根号看着不顺眼}]{x=\sin t}\int_0^{\frac{\pi}{2}} \sin ^n t \cdot \cos ^2 t d t\xrightarrow[]{\cos ^2 t =\left(1-\sin ^2 t\right)} \end{aligned} a n = ∫ 0 1 x n 1 − x 2 d x x = s i n t 根号看着不顺眼 ∫ 0 2 π sin n t ⋅ cos 2 t d t c o s 2 t = ( 1 − s i n 2 t ) = ∫ 0 π 2 sin n t d t − ∫ 0 π 2 sin n + 2 t d t \displaystyle \begin{aligned} =\int_0^{\frac{\pi}{2}} \sin ^n t d t-\int_0^{\frac{\pi}{2}} \sin ^{n+2} t d t \end{aligned} = ∫ 0 2 π sin n t d t − ∫ 0 2 π sin n + 2 t d t = ∫ 0 π 2 sin n t d t 为 I n I n − n + 1 n + 2 I n ⏟ 华里士 = 1 n + 2 I n \displaystyle \begin{aligned} \xlongequal[]{\int_0^{\frac{\pi}{2}} \sin ^n t d t\text{为}I_n}I_n-\underbrace{\frac{n+1}{n+2} I_n}_{\text{华里士}}=\frac{1}{n+2} I_n \end{aligned} ∫ 0 2 π s i n n t d t 为 I n I n − 华里士 n + 2 n + 1 I n = n + 2 1 I n ∫ 0 π 2 sin n + 2 t d t = n + 1 n + 2 ⋅ n − 1 n ⋯ 1 2 ⋅ π 2 \displaystyle \int_0^{\frac{\pi}{2}} \sin ^{n+2} t d t=\frac{n+1}{n+2} \cdot \frac{n-1}{n} \cdots \frac{1}{2} \cdot \frac{\pi}{2} ∫ 0 2 π sin n + 2 t d t = n + 2 n + 1 ⋅ n n − 1 ⋯ 2 1 ⋅ 2 π a n − 2 = 仿照 a n 写出来 ∫ 0 π 2 sin n − 2 d t − ∫ 0 π 2 sin n t d t ( n ⩾ 2 ) \displaystyle \begin{aligned}a_{n-2} \xlongequal[]{\text{仿照}a_n\text{写出来}}\int_0^{\frac{\pi}{2}} \sin ^{n-2} d t-\int_0^{\frac{\pi}{2}} \sin ^n t d t \quad(n \geqslant 2)\end{aligned} a n − 2 仿照 a n 写出来 ∫ 0 2 π sin n − 2 d t − ∫ 0 2 π sin n t d t ( n ⩾ 2 ) = I n − 2 − I n = n n − 1 I n − I n = 1 n − 1 I n \displaystyle \begin{aligned}=I_{n-2}-I_n=\frac{n}{n-1} I_n-I_n=\frac{1}{n-1} I_n\end{aligned} = I n − 2 − I n = n − 1 n I n − I n = n − 1 1 I n 两式相除,得a n a n − 2 = n − 1 n + 2 \displaystyle \begin{aligned}\frac{a_n}{a_{n-2}}=\frac{n-1}{n+2}\end{aligned} a n − 2 a n = n + 2 n − 1 由第( I) 问可知 { a n } \left\{a_n\right\} { a n } 0 < a n < a n − 1 < a n − 2 0<a_n<a_{n-1}<a_{n-2} 0 < a n < a n − 1 < a n − 2 求 lim n → ∞ a n a n − 1 → 一路放缩 \displaystyle \begin{aligned}\lim _{n \rightarrow \infty} \frac{a_{n}}{a_{n-1}}\xrightarrow[]{\text{一路放缩}}\end{aligned} n → ∞ lim a n − 1 a n 一路放缩 n − 1 n + 2 = a n a n − 2 < a n a n − 1 < a n a n = 1. \displaystyle \begin{aligned}\frac{n-1}{n+2}=\frac{a_n}{a_{n-2}}<\frac{a_n}{a_{n-1}}<\frac{a_n}{a_n}=1 .\end{aligned} n + 2 n − 1 = a n − 2 a n < a n − 1 a n < a n a n = 1. 由夹逼定理进行放缩,可得 1 = lim n → ∞ n − 1 n + 2 ⩽ lim n → ∞ a n a n − 1 ⩽ 1. \displaystyle 1=\lim _{n \rightarrow \infty} \frac{n-1}{n+2} \leqslant \lim _{n \rightarrow \infty} \frac{a_n}{a_{n-1}} \leqslant 1 . 1 = n → ∞ lim n + 2 n − 1 ⩽ n → ∞ lim a n − 1 a n ⩽ 1. 由夹逼准则可知, lim n → ∞ a n a n − 1 = 1 \displaystyle \lim _{n \rightarrow \infty} \frac{a_n}{a_{n-1}}=1 n → ∞ lim a n − 1 a n = 1 (19) (本题满分 10 分)Ω \Omega Ω x 2 + ( y − z ) 2 = ( 1 − z ) 2 ( 0 ⩽ z ⩽ 1 ) x^{2}+(y-z)^{2}=(1-z)^{2}(0 \leqslant z \leqslant 1) x 2 + ( y − z ) 2 = ( 1 − z ) 2 ( 0 ⩽ z ⩽ 1 ) z = 0 z=0 z = 0 Ω \Omega Ω
(19) (本题满分 11 分)α 1 = ( 1 , 2 , 1 ) T , α 2 = ( 1 , 3 , 2 ) T , α 3 = ( 1 , a , 3 ) T \boldsymbol{\alpha}_{1}=(1,2,1)^{\mathrm{T}}, \boldsymbol{\alpha}_{2}=(1,3,2)^{\mathrm{T}}, \boldsymbol{\alpha}_{3}=(1, a, 3)^{\mathrm{T}} α 1 = ( 1 , 2 , 1 ) T , α 2 = ( 1 , 3 , 2 ) T , α 3 = ( 1 , a , 3 ) T R 3 \mathbf{R}^{3} R 3 β = ( 1 , 1 , 1 ) T \boldsymbol{\beta}=(1,1,1)^{\mathrm{T}} β = ( 1 , 1 , 1 ) T ( b , c , 1 ) T (b, c, 1)^{\mathrm{T}} ( b , c , 1 ) T a , b , c a, b, c a , b , c α 2 , α 3 , β \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}, \boldsymbol{\beta} α 2 , α 3 , β R 3 \mathbf{R}^{3} R 3 α 2 , α 3 , β \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}, \boldsymbol{\beta} α 2 , α 3 , β α 1 , α 2 , α 3 \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3} α 1 , α 2 , α 3
(20) (1) 基的判定 \to 无关 → ∣ ⋅ ∣ ≠ 0 \displaystyle \rightarrow |\cdot| \neq 0 → ∣ ⋅ ∣ = 0 (2) 过渡矩阵 \to ( α 1 , α 2 , α 3 ) P = ( β 1 , β 2 , β 3 ) \displaystyle (\alpha_1, \alpha_2, \alpha_3) P = (\beta_1, \beta_2, \beta_3) ( α 1 , α 2 , α 3 ) P = ( β 1 , β 2 , β 3 ) (3) 基下坐标 \to γ = ( α 1 , α 2 , α 3 ) ξ \displaystyle \gamma= (\alpha_1, \alpha_2, \alpha_3) \xi γ = ( α 1 , α 2 , α 3 ) ξ 考察基下坐标γ = ( α 1 , α 2 , α 3 ) ξ \displaystyle \gamma= (\alpha_1, \alpha_2, \alpha_3) \xi γ = ( α 1 , α 2 , α 3 ) ξ ( 1 1 1 ) = ( α 1 α 2 α 3 ) ( b c 1 ) → 代入 α 1 , α 2 , α 3 ( 111 23 a 123 ) ( b c 1 ) = ( 1 1 1 ) \displaystyle \left(\begin{array}{l}1 \\1 \\1\end{array}\right)=\left(\begin{array}{lll}\alpha_1 \alpha_2 \alpha_3\end{array}\right)\left(\begin{array}{l}b \\c \\1\end{array}\right) \xrightarrow[]{\text{代入}\alpha_1 \text{,} \alpha_2 \text{,}\alpha_3}\left(\begin{array}{lll}1 1 1 \\2 3 a \\1 2 3\end{array}\right)\left(\begin{array}{l}b \\c \\1\end{array}\right)=\left(\begin{array}{l}1 \\1 \\1\end{array}\right) 1 1 1 = ( α 1 α 2 α 3 ) b c 1 代入 α 1 , α 2 , α 3 111 23 a 123 b c 1 = 1 1 1 → 写出线性方程组 { ( 1 ) b + c + 1 = 1 , ( 2 ) 2 b + 3 c + a = 1 , ( 3 ) b + 2 c + 3 = 1 , \displaystyle \xrightarrow[]{\text{写出线性方程组}}\left\{\begin{array} { l } { (1)b + c + 1 = 1 , } \\{(2) 2 b + 3 c + a = 1 , } \\{(3) b + 2 c + 3 = 1 , }\end{array} \right. 写出线性方程组 ⎩ ⎨ ⎧ ( 1 ) b + c + 1 = 1 , ( 2 ) 2 b + 3 c + a = 1 , ( 3 ) b + 2 c + 3 = 1 , (3) 式 - (1) 式可得 c = − 2 c=-2 c = − 2 再由 (1) 式可得 b = 2 b=2 b = 2 然后代入(2) 式可得 a = 3 a=3 a = 3 因此, a = 3 , b = 2 , c = − 2 a=3, b=2, c=-2 a = 3 , b = 2 , c = − 2 由于 R 3 \mathrm{R}^3 R 3 α 2 , α 3 , β \alpha_2, \alpha_3, \beta α 2 , α 3 , β R 3 \mathrm{R}^3 R 3 α 2 , α 3 , β \alpha_2, \alpha_3, \beta α 2 , α 3 , β 计算∣ α 2 , α 3 , β ∣ \displaystyle \left|\alpha_2, \alpha_3, \boldsymbol{\beta}\right| ∣ α 2 , α 3 , β ∣ \displaystyle ∣ α 2 , α 3 , β ∣ = ∣ 111 331 231 ∣ = c 2 − c 1 ∣ 101 301 211 ∣ = ( − 1 ) 3 + 2 ⋅ 1 ⋅ ∣ 11 31 ∣ \left|\alpha_2, \alpha_3, \boldsymbol{\beta}\right|=\left|\begin{array}{lll}1 1 1 \\3 3 1 \\2 3 1\end{array}\right|\xlongequal[]{c2-c1}\left|\begin{array}{lll}1 0 1 \\3 0 1 \\2 11\end{array}\right|=(-1)^{3+2} \cdot 1 \cdot\left|\begin{array}{cc}1 1 \\3 1\end{array}\right| ∣ α 2 , α 3 , β ∣ = 111 331 231 c 2 − c 1 101 301 211 = ( − 1 ) 3 + 2 ⋅ 1 ⋅ 11 31 = 2 ≠ 0 \displaystyle =2 \neq 0 = 2 = 0 行列式不等于0,秩为3,则线性无关 要计算从 α 2 , α 3 , β ⏟ 左 \underbrace{\alpha_2, \alpha_3, \beta}_{\text{左}} 左 α 2 , α 3 , β α 1 , α 0 , α 3 ⏟ 右 \underbrace{\alpha_1, \alpha_0, \alpha_3}_{\text{右}} 右 α 1 , α 0 , α 3 P P P ( α 1 , α 2 , α 3 ) = ( α 2 , α 3 , β ) P \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right)=\left(\boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3, \boldsymbol{\beta}\right) P ( α 1 , α 2 , α 3 ) = ( α 2 , α 3 , β ) P 对 ( α 2 , α 3 , β , α 1 , α 2 , α 3 ) \left(\alpha_2, \alpha_3, \boldsymbol{\beta}, \alpha_1, \alpha_2, \alpha_3\right) ( α 2 , α 3 , β , α 1 , α 2 , α 3 ) ( α 2 , α 3 , β ⏟ 起始 , α 1 , α 2 , α 3 ⏟ 目标 ) = ( 1 1 1 1 1 1 3 3 1 2 3 3 2 3 1 1 2 3 ) → r 2 − 3 r 1 r 3 − 2 r 1 ( 1 1 1 1 1 1 0 0 − 2 − 1 0 0 0 1 − 1 − 1 0 1 ) \displaystyle \begin{aligned} & \left(\underbrace{\alpha_2, \alpha_3, \boldsymbol{\beta}}_{\text{起始}}, \underbrace{\alpha_1, \alpha_2, \alpha_3}_{\text{目标}}\right)=\left(\begin{array}{lll:lll}1 & 1 & 1 & 1 & 1 &1\\3 & 3 & 1 & 2 & 3 & 3 \\2 & 3 & 1 & 1 & 2 & 3\end{array}\right) \xrightarrow[]{\begin{aligned}& r_2-3 r_1 \\& r_3-2 r_1\end{aligned}}\left(\begin{array}{cccccc}1 & 1 & 1 & 1 & 1 & 1 \\0 & 0 & -2 & -1 & 0 & 0 \\0 & 1 & -1 & -1 & 0 & 1\end{array}\right) \end{aligned} 起始 α 2 , α 3 , β , 目标 α 1 , α 2 , α 3 = 1 3 2 1 3 3 1 1 1 1 2 1 1 3 2 1 3 3 r 2 − 3 r 1 r 3 − 2 r 1 1 0 0 1 0 1 1 − 2 − 1 1 − 1 − 1 1 0 0 1 0 1 → 互换 2 , 3 两行 ( 1 1 1 1 1 1 0 1 − 1 − 1 0 1 0 0 − 2 − 1 0 0 ) → r 1 − r 2 ( 1 0 2 2 1 0 0 1 − 1 − 1 0 1 0 0 1 1 2 0 0 ) \displaystyle \begin{aligned} \xrightarrow[\text{互换}]{2\text{,}3\text{两行}}\left(\begin{array}{ccc:ccc}1 & 1 & 1 & 1 & 1 & 1 \\0 & 1 & -1 & -1 & 0 & 1 \\0 & 0 & -2 & -1 & 0 & 0\end{array}\right) \xrightarrow[]{r1-r2}\left(\begin{array}{ccc:ccc}1 & 0 & 2 & 2 & 1 & 0 \\0 & 1 & -1 & -1 & 0 & 1 \\0 & 0 & 1 & \frac{1}{2} & 0 & 0\end{array}\right)\end{aligned} 2 , 3 两行 互换 1 0 0 1 1 0 1 − 1 − 2 1 − 1 − 1 1 0 0 1 1 0 r 1 − r 2 1 0 0 0 1 0 2 − 1 1 2 − 1 2 1 1 0 0 0 1 0 → r 2 + r 3 r 1 − 2 r 3 ( 1 0 0 1 1 0 0 1 0 − 1 2 0 1 0 0 1 1 3 0 0 ) \displaystyle \begin{aligned} \xrightarrow[r_2+r_3]{r_1-2 r_3}\left(\begin{array}{lll:lll}1 & 0 & 0 & 1 & 1 & 0 \\0 & 1 & 0 & -\frac{1}{2} & 0 & 1 \\0 & 0 & 1 & \frac{1}{3} & 0 & 0\end{array}\right) \end{aligned} r 1 − 2 r 3 r 2 + r 3 1 0 0 0 1 0 0 0 1 1 − 2 1 3 1 1 0 0 0 1 0 因此, 所求过渡矩阵 P \boldsymbol{P} P ( 1 1 0 − 1 2 0 1 1 2 0 0 ) \displaystyle \left(\begin{array}{ccc}1 & 1 & 0 \\ -\frac{1}{2} & 0 & 1 \\ \frac{1}{2} & 0 & 0\end{array}\right) 1 − 2 1 2 1 1 0 0 0 1 0 (注) 在求过渡矩阵 P \boldsymbol{P} P ( α 2 , α 3 , β ) = ( α 1 , α 2 , α 3 ) P \left(\boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3, \boldsymbol{\beta}\right)=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right) \boldsymbol{P} ( α 2 , α 3 , β ) = ( α 1 , α 2 , α 3 ) P α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 α 2 , α 3 , β \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3, \boldsymbol{\beta} α 2 , α 3 , β 2015 年数一试题α 1 , α 2 , α 3 \alpha_1, \alpha_2, \alpha_3 α 1 , α 2 , α 3 R 3 \mathbf{R}^3 R 3 β 1 = 2 α 1 + 2 k α 3 \beta_1=2 \alpha_1+2 k \alpha_3 β 1 = 2 α 1 + 2 k α 3 β 2 = 2 α 2 , β 3 = α 1 + ( k + 1 ) α 3 \boldsymbol{\beta}_2=2 \boldsymbol{\alpha}_2, \quad \boldsymbol{\beta}_3=\boldsymbol{\alpha}_1+(k+1) \boldsymbol{\alpha}_3 β 2 = 2 α 2 , β 3 = α 1 + ( k + 1 ) α 3 β 1 , β 2 , β 3 \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 β 1 , β 2 , β 3 R 3 \mathrm{R}^3 R 3 k k k ξ \xi ξ α 1 , α 2 , α 3 \alpha_1, \alpha_2, \alpha_3 α 1 , α 2 , α 3 β 1 , β 2 , β 3 \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 β 1 , β 2 , β 3 ξ \boldsymbol{\xi} ξ (21) (本题满分 11 分)A = ( − 2 − 2 1 2 x − 2 0 0 − 2 ) \displaystyle \boldsymbol{A}=\left(\begin{array}{ccc}-2 & -2 & 1 \\ 2 & x & -2 \\ 0 & 0 & -2\end{array}\right) A = − 2 2 0 − 2 x 0 1 − 2 − 2 B = ( 2 1 0 0 − 1 0 0 0 y ) \displaystyle \boldsymbol{B}=\left(\begin{array}{ccc}2 & 1 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & y\end{array}\right) B = 2 0 0 1 − 1 0 0 0 y x , y x, y x , y P \boldsymbol{P} P P − 1 A P = B \boldsymbol{P}^{-1} \boldsymbol{A P}=\boldsymbol{B} P − 1 AP = B
(21) 第一问思想:相似的性质 ∣ A ∣ = ∣ B ∣ |A|=|B| ∣ A ∣ = ∣ B ∣ r ( A ) = r ( B ) r(A)=r(B) r ( A ) = r ( B ) ∣ λ E − A ∣ = ∣ λ E − B ∣ ⇒ λ A = λ B |\lambda E-A|=|\lambda E-B| \Rightarrow \lambda_A=\lambda_B ∣ λ E − A ∣ = ∣ λ E − B ∣ ⇒ λ A = λ B → \to → 这个箭头是单向的∶12年数一考的就是让同学举反例,特征值一样,但是不相似 ∑ a i i = ∑ b i i \displaystyle \sum a_{i i}=\sum b_{i i} ∑ a ii = ∑ b ii → \to → 解 (1) 由 A ∼ B ⇒ { ∣ A ∣ = ∣ B ∣ tr ( A ) = tr ( B ) r ( A ) = r ( B ) \displaystyle A \sim B \Rightarrow\left\{\begin{aligned}|A| & =|B| \\ \operatorname{tr}(A) & =\operatorname{tr}(B) \\ r(A) & =r(B)\end{aligned}\right. A ∼ B ⇒ ⎩ ⎨ ⎧ ∣ A ∣ tr ( A ) r ( A ) = ∣ B ∣ = tr ( B ) = r ( B ) 行列式的值相等计算:∣ A ∣ = 4 x − 8 , ∣ B ∣ = − 2 y \displaystyle \begin{aligned} |A| = 4x - 8, \quad |B| = -2y \end{aligned} ∣ A ∣ = 4 x − 8 , ∣ B ∣ = − 2 y 解方程组:{ 行列式的值相等 4 x − 8 = − 2 y 迹相等 : x − 4 = y + 1 \displaystyle \begin{aligned} \begin{cases}\text{行列式的值相等}4x - 8 = -2y \\\text{迹相等}:x - 4 = y + 1\end{cases}\end{aligned} { 行列式的值相等 4 x − 8 = − 2 y 迹相等 : x − 4 = y + 1 解得 x = 3 , y = − 2 x=3, y=-2 x = 3 , y = − 2 第二问思想:相似矩阵的传递性 ∃ P 1 ⋅ P 1 − 1 A P 1 = Λ \displaystyle \begin{aligned} & \exists P_1 \cdot P_1^{-1} A P_1=\Lambda \end{aligned} ∃ P 1 ⋅ P 1 − 1 A P 1 = Λ ∃ P 2 ⋅ P 2 − 1 B P 2 = Λ \displaystyle \begin{aligned} \exists P_2 \cdot P_2^{-1} B P_2=\Lambda \end{aligned} ∃ P 2 ⋅ P 2 − 1 B P 2 = Λ P 1 − 1 A P 1 = P 2 − 1 B P 2 ⇒ ( P 1 P 2 − 1 ) − 1 A ( P 1 P 2 − 1 ) = B ⇒ P = P 1 P 2 − 1 \displaystyle \begin{aligned} P_1^{-1} A P_1=P_2^{-1} B P_2 \Rightarrow\left(P_1 P_2^{-1}\right)^{-1} A\left(P_1 P_2^{-1}\right)=B \Rightarrow P=P_1 P_2^{-1} \end{aligned} P 1 − 1 A P 1 = P 2 − 1 B P 2 ⇒ ( P 1 P 2 − 1 ) − 1 A ( P 1 P 2 − 1 ) = B ⇒ P = P 1 P 2 − 1 先求特征值 λ ( A ) = λ ( B ) = 2 , − 1 , − 2 \displaystyle \lambda(A)=\lambda(B)=2,-1,-2 λ ( A ) = λ ( B ) = 2 , − 1 , − 2 求A矩阵的特征向量 ( A − 2 E ) x = 0 \displaystyle (A-2 E) x=0 \quad ( A − 2 E ) x = 0 ( − 4 − 21 21 − 2 00 − 4 ) → ( 21 − 2 00 − 3 00 − 4 ) → ( 210 001 000 ) \displaystyle \left(\begin{array}{ccc}-4 -2 1 \\2 1 -2 \\0 0 -4\end{array}\right) \rightarrow\left(\begin{array}{lll}2 1 -2 \\0 0 -3 \\0 0 -4\end{array}\right) \rightarrow\left(\begin{array}{lll}2 1 0 \\0 0 1 \\0 0 0\end{array}\right) − 4 − 21 21 − 2 00 − 4 → 21 − 2 00 − 3 00 − 4 → 210 001 000 { 2 x 1 + x 2 = 0 x 3 = 0 { x 1 = k x 2 = − 2 k x 3 = 0 x = k 1 ( 1 − 2 0 ) ( k 1 ≠ 0 ) \displaystyle \left\{\begin{array} { r l } { 2 x _ { 1 } + x _ { 2 } } & { = 0 } \\{ x _ { 3 } } & { = 0 }\end{array} \quad \left\{\begin{array}{l}x_1=k \\x_2=-2 k \\x_3=0\end{array} \quad x=k_1\left(\begin{array}{r}1 \\-2 \\0\end{array}\right)\left(k_1 \neq 0\right)\right.\right. ⎩ ⎨ ⎧ 2 x 1 + x 2 x 3 = 0 = 0 ⎩ ⎨ ⎧ x 1 = k x 2 = − 2 k x 3 = 0 x = k 1 1 − 2 0 ( k 1 = 0 ) ( A + E ) x = 0 (A+E) x=0 ( A + E ) x = 0 ( − 1 − 21 24 − 2 00 − 1 ) → ( 12 − 1 001 000 ) { x 1 + 2 x 2 − x 3 = 0 x 3 = 0 \displaystyle \left(\begin{array}{ccc}-1 -2 1 \\2 4 -2 \\0 0 -1\end{array}\right) \rightarrow\left(\begin{array}{ccc}1 2 -1 \\0 0 1 \\0 0 0\end{array}\right) \quad\left\{\begin{array}{r}x_1+2 x_2-x_3=0 \\x_3=0\end{array}\right. − 1 − 21 24 − 2 00 − 1 → 12 − 1 001 000 { x 1 + 2 x 2 − x 3 = 0 x 3 = 0 { x 1 = − 2 k x 2 = k x 3 = 0 x = k 2 ( − 2 1 0 ) ( k 2 ≠ 0 ) \displaystyle \left\{\begin{array}{l}x_1=-2 k \\x_2=k \\x_3=0\end{array} \quad x=k_2\left(\begin{array}{c}-2 \\1 \\0\end{array}\right) \quad\left(k_2 \neq 0\right)\right. ⎩ ⎨ ⎧ x 1 = − 2 k x 2 = k x 3 = 0 x = k 2 − 2 1 0 ( k 2 = 0 ) ( A + 2 E ) x = 0 (A+2 E) x=0 ( A + 2 E ) x = 0 ( 0 − 21 25 − 2 000 ) \displaystyle \left(\begin{array}{ccc}0 -2 1 \\2 5 -2 \\0 0 0\end{array}\right) 0 − 21 25 − 2 000 { 2 x 1 + 5 x 2 − 2 x 3 = 0 − 2 x 2 + x 3 = 0 { x 1 = k x 2 = − 2 k x 3 = − 4 k x = k 3 ( 1 − 2 − 4 ) \displaystyle \left\{\begin{array} { r } { 2 x _ { 1 } + 5 x _ { 2 } - 2 x _ { 3 } = 0 } \\{ - 2 x _ { 2 } + x _ { 3 } = 0 }\end{array} \quad \left\{\begin{array}{ll}x_1=k \\x_2= & -2 k \\x_3=-4 k\end{array} \quad x=k_3\left(\begin{array}{c}1 \\-2 \\-4\end{array}\right)\right.\right. ⎩ ⎨ ⎧ 2 x 1 + 5 x 2 − 2 x 3 = 0 − 2 x 2 + x 3 = 0 ⎩ ⎨ ⎧ x 1 = k x 2 = x 3 = − 4 k − 2 k x = k 3 1 − 2 − 4 求B矩阵的特征向量 ( B − 2 E ) x = 0 ( 0 1 0 0 − 3 0 0 0 − 4 ) → ( 0 1 0 0 0 1 0 0 0 ) x = k 4 ( 1 0 0 ) k 4 ≠ 0 \displaystyle (B-2 E) x=0 \quad\left(\begin{array}{ccc}0 & 1 & 0 \\0 & -3 & 0 \\0 & 0 & -4\end{array}\right) \rightarrow\left(\begin{array}{lll}0 & 1 & 0 \\0 & 0 & 1 \\0 & 0 & 0\end{array}\right) \quad x=k_4\left(\begin{array}{l}1 \\0 \\0\end{array}\right) \quad k_4 \neq 0 ( B − 2 E ) x = 0 0 0 0 1 − 3 0 0 0 − 4 → 0 0 0 1 0 0 0 1 0 x = k 4 1 0 0 k 4 = 0 ( B + E ) x = 0 ( 3 1 0 0 0 0 0 0 − 1 ) → ( 3 1 0 0 0 1 0 0 0 ) x = k 5 ( 1 − 3 0 ) k 5 ≠ 0 \displaystyle (B+E) x=0 \quad\left(\begin{array}{ccc}3 & 1 & 0 \\0 & 0 & 0 \\0 & 0 & -1\end{array}\right) \rightarrow\left(\begin{array}{ccc}3 & 1 & 0 \\0 & 0 & 1 \\0 & 0 & 0\end{array}\right) \quad x=k_5\left(\begin{array}{c}1 \\-3 \\0\end{array}\right) \quad k_5 \neq 0 ( B + E ) x = 0 3 0 0 1 0 0 0 0 − 1 → 3 0 0 1 0 0 0 1 0 x = k 5 1 − 3 0 k 5 = 0 ( B + 2 E ) x = 0 ( 4 1 0 0 1 0 0 0 0 ) → ( 1 0 0 0 1 0 0 0 0 ) x = k b ( 0 0 1 ) k 6 ≠ 0 \displaystyle (B+2 E) x=0 \quad\left(\begin{array}{lll}4 & 1 & 0 \\0 & 1 & 0 \\0 & 0 & 0\end{array}\right) \rightarrow\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 0\end{array}\right) \quad x=k_b\left(\begin{array}{l}0 \\0 \\1\end{array}\right) \quad k_6 \neq 0 ( B + 2 E ) x = 0 4 0 0 1 1 0 0 0 0 → 1 0 0 0 1 0 0 0 0 x = k b 0 0 1 k 6 = 0 P 1 − 1 A P 1 = P 2 − 1 B P 2 → 用对角矩阵传递 传递性 ( P 1 P 2 − 1 ) − 1 A ( P 1 P 2 − 1 ) = B \displaystyle P_1^{-1} A P_1=P_2^{-1} B P_2 \xrightarrow[\text{用对角矩阵传递}]{\text{传递性}}\quad\left(P_1 P_2^{-1}\right)^{-1} A\left(P_1 P_2^{-1}\right)=B P 1 − 1 A P 1 = P 2 − 1 B P 2 传递性 用对角矩阵传递 ( P 1 P 2 − 1 ) − 1 A ( P 1 P 2 − 1 ) = B P = P 1 P 2 − 1 = ( 1 − 21 − 21 − 2 00 − 4 ) ( 110 0 − 30 001 ) − 1 \displaystyle P=P_1 P_2^{-1}=\left(\begin{array}{ccc}1 -2 1 \\-2 1 -2 \\0 0 -4\end{array}\right)\left(\begin{array}{ccc}1 1 0 \\0 -3 0 \\0 0 1\end{array}\right)^{-1} P = P 1 P 2 − 1 = 1 − 21 − 21 − 2 00 − 4 110 0 − 30 001 − 1 ( 1 1 0 0 − 3 0 0 0 1 ∣ 1 0 0 0 1 0 0 0 1 ) → r 1 − r 2 r 2 ⋅ − 1 3 ( 1 0 0 0 1 0 0 0 1 ∣ 1 1 3 0 0 − 1 3 0 0 0 1 ) \displaystyle \left.\left(\begin{array}{ccc}1 & 1 & 0 \\0 & -3 & 0 \\0 & 0 & 1\end{array}\right| \begin{array}{lll}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) \xrightarrow[r_1-r_2]{r_2 \cdot-\frac{1}{3}}\left(\begin{array}{ccc|ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array} \left\lvert\, \begin{array}{ccc}1 & \frac{1}{3} & 0 \\0 & -\frac{1}{3} & 0 \\0 & 0 & 1\end{array}\right.\right) 1 0 0 1 − 3 0 0 0 1 1 0 0 0 1 0 0 0 1 r 2 ⋅− 3 1 r 1 − r 2 1 0 0 0 1 0 0 0 1 1 0 0 3 1 − 3 1 0 0 0 1 P = ( 1 − 2 1 − 2 1 − 2 0 0 − 4 ) ( 1 1 3 0 0 − 1 3 0 0 0 1 ) = ( 1 1 1 − 2 − 1 − 2 0 0 − 4 ) \displaystyle P=\left(\begin{array}{ccc}1 & -2 & 1 \\-2 & 1 & -2 \\0 & 0 & -4\end{array}\right)\left(\begin{array}{ccc}1 & \frac{1}{3} & 0 \\0 & -\frac{1}{3} & 0 \\0 & 0 & 1\end{array}\right)=\left(\begin{array}{ccc}1 & 1 & 1 \\-2 & -1 & -2 \\0 & 0 & -4\end{array}\right) P = 1 − 2 0 − 2 1 0 1 − 2 − 4 1 0 0 3 1 − 3 1 0 0 0 1 = 1 − 2 0 1 − 1 0 1 − 2 − 4 A \boldsymbol{A} A B \boldsymbol{B} B A = ( − 2 0 0 2 x 2 3 1 1 ) , B = ( − 1 0 0 0 2 0 0 0 y ) . \displaystyle \boldsymbol{A}=\left(\begin{array}{ccc}-2 & 0 & 0 \\2 & x & 2 \\3 & 1 & 1\end{array}\right), \quad \boldsymbol{B}=\left(\begin{array}{ccc}-1 & 0 & 0 \\0 & 2 & 0 \\0 & 0 & y\end{array}\right) . A = − 2 2 3 0 x 1 0 2 1 , B = − 1 0 0 0 2 0 0 0 y . x x x y y y P P P P − 1 A P = B P^{-1} A P=B P − 1 A P = B (22) (本题满分 11 分)X X X Y Y Y X X X Y Y Y P { Y = − 1 } = p P\{Y=-1\}=p P { Y = − 1 } = p P { Y = 1 } = 1 − p ( 0 < p < 1 ) P\{Y=1\}=1-p(0<p<1) P { Y = 1 } = 1 − p ( 0 < p < 1 ) Z = X Y Z=X Y Z = X Y Z Z Z p p p X X X Z Z Z X X X Z Z Z
(22) 分析 本题主要考查随机变量的函数的概率密度, 随机变量不相关及相互独立的概念. 第 (I) 问中, Z Z Z 可先根据定义计算 Z Z Z 再求导得到概率密度. 第(II)问中,可利用 X X X Z Z Z Cov ( X , Z ) = 0 \operatorname{Cov}(X, Z)=0 Cov ( X , Z ) = 0 p p p 第 (III) 问中, 判断两个随机变量是否相互独立, 可根据相互独立的定义判断a , b a, b a , b P { X ⩽ a , Z ⩽ b } = P { X ⩽ a } ⋅ P { Z ⩽ b } P\{X \leqslant a, Z \leqslant b\}=P\{X \leqslant a\} \cdot P\{Z \leqslant b\} P { X ⩽ a , Z ⩽ b } = P { X ⩽ a } ⋅ P { Z ⩽ b } 若存在 a , b a, b a , b X X X Z Z Z X是连续型:由于 X X X 故 X X X f X ( x ) = { e − x , x > 0 , 0 , x ≤ 0. \displaystyle f_X(x)=\left\{\begin{array}{ll}\mathrm{e}^{-x}, & x>0, \\ 0, & x \leq 0 .\end{array}\right. f X ( x ) = { e − x , 0 , x > 0 , x ≤ 0. X的分布函数:F x ( x ) = { 0 x < 0 1 − e − x 0 ⩽ x \displaystyle F_x(x)=\left\{\begin{array}{cc}0 & x<0 \\ 1-e^{-x} & 0 \leqslant x\end{array}\right. F x ( x ) = { 0 1 − e − x x < 0 0 ⩽ x Y是离散型:而 P { Y = − 1 } = p , P { Y = 1 } = 1 − p P\{Y=-1\}=p, P\{Y=1\}=1-p P { Y = − 1 } = p , P { Y = 1 } = 1 − p Z = X Y Z=X Y Z = X Y Z Z Z F Z ( z ) = 定义 P { Z ⩽ z } = 转化 Z = X Y P { X Y ⩽ z } \left.F_Z(z)\xlongequal[]{\text{定义}}P\{Z \leqslant z\}\xlongequal[]{\text{转化}Z=XY}P\{X Y \leqslant z\}\right. F Z ( z ) 定义 P { Z ⩽ z } 转化 Z = X Y P { X Y ⩽ z } = 对离散的全集分解 P ( X Y ⩽ z , Y = − 1 ) + P { X Y ⩽ z , Y = 1 } \xlongequal[]{\text{对离散的全集分解}}P(X Y \leqslant z, Y=-1)+P\{X Y \leqslant z, Y=1\} 对离散的全集分解 P ( X Y ⩽ z , Y = − 1 ) + P { X Y ⩽ z , Y = 1 } = 代入 Y 的值 P { − X ⩽ z , Y = − 1 } + P { X ⩽ z , Y = 1 } \xlongequal[]{\text{代入}Y\text{的值}}P\{-X \leqslant z, Y=-1\}+P\{X \leqslant z, Y=1\} 代入 Y 的值 P { − X ⩽ z , Y = − 1 } + P { X ⩽ z , Y = 1 } = X 与 Y 独立 P { X ⩾ − z } P { Y = − 1 } + P { X ⩽ z } P { Y = 1 } \xlongequal[]{X\text{与}Y\text{独立}}P\{X \geqslant-z\} P\{Y=-1\}+P\{X \leqslant z\} P\{Y=1\} X 与 Y 独立 P { X ⩾ − z } P { Y = − 1 } + P { X ⩽ z } P { Y = 1 } = 代入离散型的概率 p P { X ⩾ − z } + ( 1 − p ) P { X ⩽ z } \xlongequal[]{\text{代入离散型的概率}}p P\{X \geqslant-z\}+(1-p) P\{X \leqslant z\} 代入离散型的概率 pP { X ⩾ − z } + ( 1 − p ) P { X ⩽ z } P { x ⩾ − z } = 1 − F x ( − z ) \displaystyle P\{x \geqslant-z\}=1-F_x(-z) P { x ⩾ − z } = 1 − F x ( − z ) F x ( − z ) = { 0 z > 0 1 − e z z ⩽ 0 \displaystyle F_x(-z)=\left\{\begin{array}{cc}0 & z>0 \\1-e^z & z \leqslant 0\end{array}\right. F x ( − z ) = { 0 1 − e z z > 0 z ⩽ 0 P { x ⩾ − z } = { 1 z > 0 e z z ⩽ 0 \displaystyle P\{x \geqslant-z\}=\left\{\begin{array}{cc}1 & z>0 \\e^z & z \leqslant 0\end{array}\right. P { x ⩾ − z } = { 1 e z z > 0 z ⩽ 0 P { x ⩽ z } = F x ( z ) \displaystyle P\{x \leqslant z\} =F_x(z) P { x ⩽ z } = F x ( z ) = { 0 z < 0 1 − e − z 0 ⩽ z \displaystyle =\left\{\begin{array}{cc}0 & z<0 \\1-e^{-z} & 0 \leqslant z\end{array}\right. = { 0 1 − e − z z < 0 0 ⩽ z 将对应区域叠加,得到z的分布函数 (1) z < 0 z<0 z < 0 F z ( z ) = P ⋅ e z \quad F_z(z)=P \cdot e^z F z ( z ) = P ⋅ e z (2) 0 ⩽ z 0 \leqslant z 0 ⩽ z F z ( z ) = p + ( 1 − p ) ( 1 − e − z ) = 1 − ( 1 − p ) e − z \quad F_z(z)=p+(1-p)\left(1-e^{-z}\right)=1-(1-p) e^{-z} F z ( z ) = p + ( 1 − p ) ( 1 − e − z ) = 1 − ( 1 − p ) e − z z的分布函数求导,得到概率密度 f z ( z ) = { P e z z < 0 ( 1 − p ) e − z 0 ⩽ z \displaystyle f_z(z)= \begin{cases}P e^z & z<0 \\ (1-p) e^{-z} & 0 \leqslant z\end{cases} f z ( z ) = { P e z ( 1 − p ) e − z z < 0 0 ⩽ z (23) (本题满分 11 分)X X X
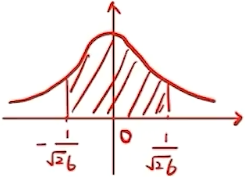
f ( x ; σ 2 ) = { A σ e − ( x − μ ) 2 2 σ 2 , x ⩾ μ , 0 , x < μ , \displaystyle f\left(x ; \sigma^{2}\right)= \begin{cases}\frac{A}{\sigma} \mathrm{e}^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}, & x \geqslant \mu, \\ 0, & x<\mu,\end{cases} f ( x ; σ 2 ) = { σ A e − 2 σ 2 ( x − μ ) 2 , 0 , x ⩾ μ , x < μ , μ \mu μ σ > 0 \displaystyle \sigma>0 σ > 0 A A A X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n X X X A A A σ 2 \displaystyle \sigma^{2} σ 2 (23) 解 (1) 由 ∫ − ∞ + ∞ f ( x ; σ 2 ) d x = 1 \displaystyle \int_{-\infty}^{+\infty} f\left(x ; \sigma^2\right) \mathrm{d} x=1 ∫ − ∞ + ∞ f ( x ; σ 2 ) d x = 1 1 = ∫ μ + ∞ A σ e − ( x − μ ) 2 2 σ 2 d x = A ∫ 0 + ∞ e − t 2 2 d t = A ⋅ 2 π 2 ∫ − ∞ + ∞ 1 2 π e − t 2 2 d t = 2 π 2 A , \displaystyle 1=\int_\mu^{+\infty} \frac{A}{\sigma} \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}} \mathrm{~d} x=A \int_0^{+\infty} \mathrm{e}^{-\frac{t^2}{2}} \mathrm{~d} t=A \cdot \frac{\sqrt{2 \pi}}{2} \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{t^2}{2}} \mathrm{~d} t=\frac{\sqrt{2 \pi}}{2} A, 1 = ∫ μ + ∞ σ A e − 2 σ 2 ( x − μ ) 2 d x = A ∫ 0 + ∞ e − 2 t 2 d t = A ⋅ 2 2 π ∫ − ∞ + ∞ 2 π 1 e − 2 t 2 d t = 2 2 π A , 所以 A = 2 π A=\sqrt{\frac{2}{\pi}} A = π 2 设 x 1 , x 2 , ⋯ , x n x_{1}, x_{2}, \cdots, x_{n} x 1 , x 2 , ⋯ , x n 写出似然函数为L ( σ 2 ) = ∏ i = 1 n f ( x ; σ 2 ) = { ( 2 x ) n ⋅ 1 σ n \cdotp e − 1 2 σ 2 ∑ i = 1 n ( x − μ ) 2 x ≥ μ 0 \displaystyle L\left(\sigma^2\right)=\prod_{i=1}^n f\left(x ; \sigma^2\right)=\left\{\begin{array}{c}\left(\sqrt{\frac{2}{x}}\right)^n \cdot \frac{1}{\sigma^n}\text{·} e^{-\frac{1}{2 \sigma^2} \sum_{i=1}^n(x-\mu)^2} \quad x \geq\mu \\ 0\end{array}\right. L ( σ 2 ) = i = 1 ∏ n f ( x ; σ 2 ) = { ( x 2 ) n ⋅ σ n 1 \cdotp e − 2 σ 2 1 ∑ i = 1 n ( x − μ ) 2 x ≥ μ 0 取对数:ln L ( σ 2 ) = n ln ( 2 π ) − n ln 1 σ ⏟ 看作 n 2 ln ( σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 \displaystyle \ln L\left(\sigma^2\right)=n \ln \left(\sqrt{\frac{2}{\pi}}\right)-\underbrace{n \ln \frac{1}{\sigma}}_{\text{看作}\frac{n}{2} \ln \left(\sigma^2\right)}-\frac{1}{2 \sigma^2} \sum_{i=1}^n\left(x_i-\mu\right)^2 ln L ( σ 2 ) = n ln ( π 2 ) − 看作 2 n l n ( σ 2 ) n ln σ 1 − 2 σ 2 1 i = 1 ∑ n ( x i − μ ) 2 对σ 2 \displaystyle \sigma^{2} σ 2 d ln L ( σ 2 ) d ( σ 2 ) = − n 2 1 σ 2 + 1 2 ( σ 2 ) 2 ∑ i = 1 n ( x i − μ ) 2 = 0 \displaystyle \frac{d \ln L\left(\sigma^{2}\right)}{d\left(\sigma^{2}\right)}=-\frac{n}{2} \frac{1}{\sigma^{2}}+\frac{1}{2\left(\sigma^{2}\right)^{2}} \sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2}=0 d ( σ 2 ) d ln L ( σ 2 ) = − 2 n σ 2 1 + 2 ( σ 2 ) 2 1 i = 1 ∑ n ( x i − μ ) 2 = 0 移项: → 通分 ∑ i = 1 n ( x i − μ ) 2 2 σ 4 = n σ 2 2 σ 4 \displaystyle \xrightarrow[]{\text{通分}}\frac{\sum_{i=1}^n\left(x_i-\mu\right)^2}{2\sigma^4}=\frac{n \sigma^2}{2\sigma^4} 通分 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 2 σ 4 n σ 2 σ 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 \displaystyle \sigma^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2} σ 2 = n 1 i = 1 ∑ n ( x i − μ ) 2 故 σ 2 \displaystyle \sigma^{2} σ 2 量 为 σ ^ 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 \displaystyle \hat{\sigma}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2} σ ^ 2 = n 1 i = 1 ∑ n ( X i − μ ) 2