一、选择题:1 10 小题, 每小题 5 分, 共 50 分。下列每题给出的四个选项中, 只有一个选项是最符合题目要求的,请将所选项前的字母填在答题纸指定位置上。
(1)
已知函数 f(x)=∫0xecostdt,g(x)=∫0sinxet2dt, 则 ( )
(A) f(x) 是奇函数, g(x) 是偶函数
(B) f(x) 是偶函数, g(x) 是奇函数
(C) f(x) 与 g(x) 均为奇函数
(D) f(x) 与 g(x) 均为周期函数
李艳芳真题系列|考研数学一历年真题逐题精讲(2010-2024年)[更新至最新]-哔哩哔哩
- 读题:已知函数 函数积分和求导后,奇偶性会发生改变f(x)=∫0xecostdt,g(x)=∫0sinxet2dt, 则 ( )
- ecosx 是偶函数,ecos(−x)=ecosx
- f(x)=∫0xecostdt是奇函数
- et2 是偶函数
- h(x)=∫0xet2dt是奇函数
- g(−x)=h(sin(−x))=h(−sinx)=−h(sinx)=−g(x)
- h(sinx)=∫0sinxet2dt是奇函数
- 若 f(x) 是连续函数, F(x)=∫0xf(t)dtF(x)是f(x)的一个原函数,
- 则当 f(x) 是奇函数时, F(x) 必是偶函数,
- 当 f(x) 是偶函数时,当且仅当 F(0)=0 时, F(x) 是奇函数.
- 小结:判定奇偶及周期性
- (1) 用定义,如,证明
- f(x)=∫xx+2π∣sint∣dt 以 π 为周期
- F(x)=∫−aa∣x−a∣f(t)dt 与 f(x) 的奇偶性一致
- (2) 用结论
- 复合函数 f[g(x)],内 (g(x)) 偶则偶,内 (g(x)) 奇同外
- 内部是偶函数,则复合函数也是偶函数,
- 内部是奇函数,则奇偶性取决于外层函数
- 求导改变奇偶性,但不改变周期性
- ∫0xf(t)dt 的奇偶性与 f(x) 的计算奇偶性相反
- f(x) 以 T 为周期,若 ∫0Tf(t)dt=0,则 ∫x0xf(t)dt 也以 T 为周期
1999 年数一、二、三试题
设 f(x) 是连续函数, F(x) 是 f(x) 的原函数,则( )
(A) 当 f(x) 是奇函数时, F(x) 必是偶函数。
(B)当 f(x) 是偶函数时, F(x) 必是奇函数。
(C) 当 f(x) 是周期函数时, F(x) 必是周期函数。
(D) 当 f(x) 是单调增函数时, F(x) 必是单调增函数.
2005 年数一、二试题
设 F(x) 是连续函数 f(x) 的一个原函数, " M⇔N "表示 " M 的充分必要条件是 N′′ ,则必有()
(A) F(x) 是偶函数 ⇔f(x) 是奇函数.
(B) F(x) 是奇函数 ⇔f(x) 是偶函数.
(C) F(x) 是周期函数 ⇔f(x) 是周期函数.
(D) F(x) 是单调函数 ⇔f(x) 是单调函数.
2024 年数二试题
设函数 f(x)=∫0sinxsint3 dt,g(x)=∫0xf(t)dt ,则 ()
(A) f(x) 是奇函数, g(x) 是奇函数.
(B) f(x) 是奇函数, g(x) 是偶函数。
(C) f(x) 是偶函数, g(x) 是偶函数.
(D) f(x) 是偶函数, g(x) 是奇函数.
(2)
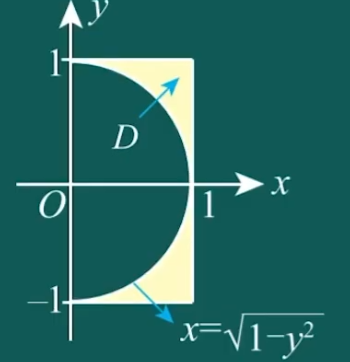
设 P=P(x,y,z),Q=Q(x,y,z) 均为连续函数, Σ 为曲面 Z=1−x2−y2(x⩽0,y⩾0) 的上侧,则 ∬ΣPdydz+Qdzdx=()
(A) ∬Σ(zxP+zyQ)dxdy
(B) ∬Σ(−zxP+zyQ)dxdy
(C) ∬Σ(zxP−zyQ)dxdy
(D) ∬Σ(−zxP−zyQ)dxdy
- 读题
设 P=P(x,y,z),Q=Q(x,y,z) 均为连续函数, Σ 为画图+球面曲面Z=1−x2−y2(x⩽0,y⩾0)的上侧,则 第二类曲面积分∬ΣPdydz+Qdzdx=() - 解:Σ∬Pdydz+Qdxdz+Rdxdy转换投影法Σ∬[P⋅(−∂x∂z)+Q⋅(−∂y∂z)+R]dxdy
- 本题曲面 Σ 方程为 z=1−x2−y2,于是
- ∂x∂z=1−x2−y2−x=z−x
- ∂y∂z=z−y
- 按照上述公式,选 (A)。
(3)
设幕级数 n=0∑∞anxn 的和函数为 ln(2+x), 则 n=0∑∞na2n ( )
(A) −61
(B) −31
(C) 61
(D) 31
- 读题:
设已知和函数,反求幂级数的系数幂级数n=0∑∞anxn的和函数为ln(2+x)ln(1+x)=∑n=1∞n(−1)n−1xn, 则 n=0∑∞na2n ( ) - ln(1+x)=x−2x2+⋯+n(−1)n−1xn+⋯=n=1∑∞n(−1)n−1xn(−1<x≤1)
- 解:展开的关键在“变形”,由于
ln(2+x)恒等变形ln2(1+2x)=ln2+ln(1+2x)- 幂级数展开ln(1+x)=∑n=1∞n(−1)n−1xnln2+n=1∑∞(−1)n−1n(2x)n整理∑n=0∞anxnln2+n=1∑∞(−1)n−1n⋅2n1xn
- =n=0∑∞anxn拆出1到∞a0+n=1∑∞anxn
- 所以 a0=ln2,an=(−1)n−1n⋅2n1,n=1,2,⋯
- 将n换成2nn=0∑∞na2n0×a2n=00项没用n=1∑∞na2n=n=1∑∞n⋅(−1)2n−12n⋅22n1
- 整理−n=1∑∞22n+11=−(231+251+271+⋯)等比数列求和−1−221231=−61
- 小结:如何找复杂函数 f(x) 的幂级数展开式?
- (1) 将 f(x) 初等变形化成常用函数,然后套基本公式;
- (2) 将 f(x) 先求导化成常用函数,然后套基本公式;
- (3) 将 f(x) 先积分化成常用函数,然后套基本公式。
(4)
设函数 f(x) 在区间上 (−1,1) 有定义, 且 x→0limf(x)=0, 则 ( )
(A) 当 x→0limxf(x)=m 时, f′(0)=m
(B) 当 f′(0)=m 时, x→0limxf(x)=m
(C) 当 x→0limf′(x)=m 时, f′(0)=m
(D) 当 f′(0)=m 时, x→0limf′(x)=m
解:
- A:x→0limf(x)=0,未必有 f(0)=0
- 故 (A) 选项 x→0limxf(x)=mf(0)的值未知未必有 x→0limxf(x)−f(0)=m。
- B:当 f′(0)=m 时,必有 f(x) 在 0 点连续,于是由 x→0limf(x)=0,必有 f(0)=0,
- 此时 f′(0)=x→0limxf(x)−f(0)=x→0limxf(x)f(0)=0m
- 对 (C) 和 (D),当 f(x) 在 0 点连续时,
- 若 x→0limf′(x)=m(可以是 ∞),此时有 f′(0)=m(可以是 ∞),
- 但反之不成立,也就是说,若 f′(0)=m,此时未必有 x→0limf′(x)=m。
- 且还应知道,若 x→0limf′(x) 不存在(非 ∞),此时未必有 f′(0) 也不存在。
- 以上所述便是“连续函数的导函数极限定理”,在 2009 年真题已证明过。
(5)
在空间直角坐标系 O−xyz 中, 三张平面 πi:aix+biy+ciz=di(i=1,2,3) 的位置关系如图所示,记 αi=(ai,bi,ci),βi=(ai,bi,ci,di) 若 rα1α2α3=m,rβ1β2β3=n, 则 (,
(A) m=1,n=2
(B) m=n=2
(C) m=2,n=3
(D) m=n=3
- 解:由题意可知,π1,π2,π3 相交于一条直线,且不重合,
- 于是方程组⎩⎨⎧a1x+b1y+c1z=d1,a2x+b2y+c2z=d2,a3x+b3y+c3z=d3有无穷多解。
- 无穷多解要求(1)系数矩阵和增广矩阵的秩相等,(2)秩< n
- 只有B选项符合要求
- π1,π2,π3 相交于一个点,则有唯一解
- 唯一解要求(1)系数矩阵和增广矩阵的秩相等,(2)秩= n
- 只有D选项符合要求
(6)
设向量 α1=a1−11,α2=11ba,α3=1a−11, 若 α1,α2,α3 线性相关, 且其中任意两个向量均线性无关,则( )
(A) a=1,b=1
(B) a=1,b=−1
(C) a=2,b=2
(D) a=−2,b=2
- 读题
设向量 α1=a1−11,α2=11ba,α3=1a−11, 若 r(α1,α2,α3)≤2α1,α2,α3线性相关, 且其中r(α1,α2,α3)⩾2任意两个向量均线性无关,则( ) - 解:显然 a=1 时,α1=α3,这与 α1,α2,α3 中任意两个向量都无关矛盾!
- 先算秩
- α1,α2,α3 线性相关,得到r(α1,α2,α3)≤2
- 其中任意两个向量均线性无关,得到r(α1,α2,α3)⩾2
- 从而r(α1,α2,α3)=2
- 初等行变化
- (α1,α2,α3)=a1−111bba1a−11行变化11−1a1ab1a1−11
- 第一行加到2,3,4行10001a−1b+11−aa1−aa−11−a2第二行加到第四行10001a−1b+10a1−aa−12−a−a2
- 求a的值
- 2−a−a2=0⇒−(a+2)(a−1)=0
- r(α1,α2,α3)=2第四行全02−a−a2=0⇒a=1或a=−2.
- a=1时,100c10b+101000,α1,α3线性相关,和题意不合
- a=−2时,原式a=−210001−3b+10−23−30第二行加到第三行10001−3b−20−2300
- r(α1,α2,α3)=2⇒b−2=0 则 b=2
(7)
设 A 是秩为 2 的 3 阶矩阵, α 是满足 Aα=0 的非零向量, 若对满足 βTα=0 的 3 维向量 β 均有 Aβ=β, 则()
(A) A3 的迹为 2
(B) A3 的迹为 5
(C) A2 的迹为 8
(D) A2 的迹为 9
解:
- 读题
设 A 是秩为 2 的 3 阶矩阵, 一个特征值为0α是满足Aα=0的非零向量, 若对满足 βTα=0 的 另外两个特征值都是13维向量β均有Aβ=β, 则() - 得出特征值0有两个方法
- r(A)=2<3,于是 ∣A∣=0,于是 λ1=0。
- Aα=0 (a=0) \to a 是 A 的属于0的一个特征向量。
- 求另外两个特征值
- βTα=0 \to αTβ=0 (β 是 αTx=0 的解)
- 因为只有一个方程,所以αTx=0 有非零解 β1,β2。
- Aβ1=β1,Aβ2=β2,由特征向量的定义得出特征值
- 据 Aβ=β,得 Aβ1=β1=1⋅β1,且 Aβ2=β2=1⋅β2。
- 则 β1,β2 为特征值 λ2=λ3=1 的线性无关特征向量,
- A 有三个特征向量 β1,β2,α,特征值为 1,1,0。
- 所以 tr(An)=0+1+1=2
(8)
设随机变量 X,Y 相互独立, 且 X∼N(0,2),Y∼N(−2,2), 若 P{2X+Y<a}=P{X>Y},则 a=()
(A) −2−10
(B) −2+10
(C) −2−6
(D) −2+6
- 读题
设随机变量 X,Y 相互独立, 且 X,Y的期望E和方差DX∼N(0,2),Y∼N(−2,2), 若 用标准化求正态分布的概率P{2X+Y<a}正态分布的线性组合也服从正态=P{X>Y},则 a=() - 2X+Y,Y−X也服从正态分布
分别由X和Y的期望方差来计算,这两个分布的期望和方差 - 2X+Y
- E(2X+Y)提出系数2EX+EY=0+(−2)=−2
- D(2X+Y)提出系数4DX+DY=4×2+2=10
- 于是 2X+Y∼N(−2,10)标准化102X+Y+2∼N(0,1)
- X>Y
- E(Y−X)=E(Y)−E(X)=−2−0=−2
- D(Y−X)=D(Y)+D(X)=2+2=4
- 同理可算得 Y−X∼N(−2,4)标准化2Y−X+2∼N(0,1)
- 标准化步骤F(x)=P{X≤x}=P{σX−μ≤σx−μ}=Φ(σx−μ)
- P{2X+Y<a}标准化P{102X+Y+2<10a+2}=Φ(10a+2),
- P{X>Y}=P{Y−X<0}标准化P{2Y−X+2<22}=Φ(1)
- 由P{2X+Y<a}=P{X>Y},得10a+2=1, 得 a=10−2
- ★正态分布的标准化: 若 X∼N(μ,σ2), 则 Z=σX−μ∼N(0,1). 于是有
- X≤x
- F(x)=P{X≤x}=P{σX−μ≤σx−μ}=Φ(σx−μ)
- 举例:X 分布函数 Φ(4x−2)⇒X∼N(2,42)
- 举例2:∫−∞+∞φ(4x−2)dxFx(x)∼N(2,42)=4∫−∞+∞41φ(4x−2)dx=4
- a<X≤b
- P{a<X≤b}不等式三端同时标准化X减μ除σP{σa−μ<σX−μ≤σb−μ}=Φ(σb−μ)−Φ(σa−μ)
- ∣X∣⩽a
- P{∣X∣⩽a}=Φ(σa−μ)−Φ(σ−a−μ);
(9)
设随机变量 X 的概率密度为 f(x)={2(1−x),0<x<10, 其他 , 在 X=x(0<x<1) 的条件下, 随机变量 Y 服从区间 (x,1) 上的均匀分布, 则 Cov(X,Y)=()
(A) −361
(B) −721
(C) 721
(D) 361
- 读题
设随机变量 用来求E(X)和E(X2)和方差D(X)X的概率密度为f(x)={2(1−x),0<x<10, 其他 , 在 X=x(0<x<1) 的条件下, 随机变量 Y 服从区间 (x,1) 上的均匀分布, 则 Cov(X,Y)=E(XY)−E(X)E(Y)Cov(X,Y)=()
亚当夏娃
- Cov(X,Y)=E(XY)−E(X)E(Y)
- E(x)=∫−∞+∞xf(x)dx=∫01x⋅2(1−x)dx
- =∫01(2x−2x2)dx=(x2−32x3)01=31
- E(X2)=∫−∞+∞x2f(x)dx=2∫01x2⋅(1−x)dx
- =2∫01(x2−x3)dx=2(3x3−4x4)01
- =2⋅(31−41)=61
- D(X)=E(X2)-[E(X)]2=61−91=181
- 在 X=x(0<x<1) 的条件下, 随机变量 Y 服从区间 (x,1) 上的均匀分布
Y∣X∼U(X,1)- E(Y∣X)=21+X, D(Y∣X)=12(1−X)2
- EX=2a+b,D(X)=12(b−a)2
- Cov(X,Y)=E(XY)−E(X)E(Y)=41−21⋅32=361
- E(Y)=E(E(Y∣X))=E(21+X)=E(21)+21E(X)=21+21⋅31=32
- E(XY)=E(E(XY∣X))=E(X·E(Y∣X))=E(X·21+X)
- =E(2X+X2)=21E(X)+21E(X2)=21·31+21⋅61=41
常规法
- 由题意可知
- f(x)={2(1−x),0<x<1,0,其他,
- fY∣X(y∣x)={1−x1,x<y<1,0,其他.
- 于是 f(x,y)=f(x)⋅fY∣X(y∣x)={2,0<x<y<1,0,其他.
- Cov(X,Y)=E(XY)−E(X)E(Y)
- EX=∫012x(1−x)dx=2×(21−31)=31,
- EY=∫01dx∫x12ydy=∫01(1−x2)dx=32.
- E(XY)=∫01dx∫x12xydy=∫01x(1−x2)dx=41,
- 于是Cov(X,Y)=E(XY)−EX⋅EY==41−92=361.
(10)
设随机变量 X,Y 相互独立,且均服从参数为 λ 的指数分布,令 Z=∣X−Y∣ ,则下列随机变量中与 Z 同分布的是
(A) X+Y
(B) 2X+Y
(C) 2X
(D) X
- X的概率密度 f(x)={λe−λx,x>00,x≤0
- Y的概率密度f(y)={λe−λy,y>00,y≤0
- X 与 Y 的联合概率密度为 f(x,y)=fX(x)⋅fY(y)={λ2e−λ(x+y),x>0,y>0,0,其他.
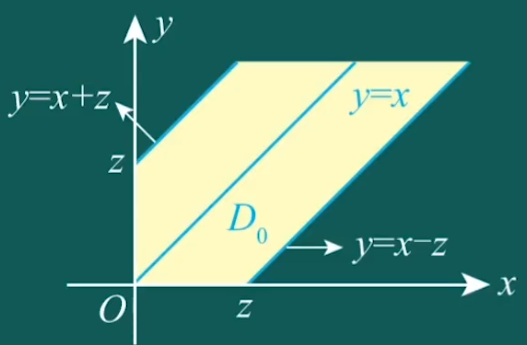
- 设 Z 的分布函数为 FZ(z),则 FZ(z)=P{Z⩽z}=P{∣X−Y∣⩽z}。
- (1) 当 z<0 时绝对值不可能小于一个负数因此概率为零FZ(z)=0;
- (2) 当 z⩾0 时,FZ(z)=P{∣X−Y∣≤z}去绝对值P{−z≤X−Y≤z}
- =P{x−z≤y≤x+z}
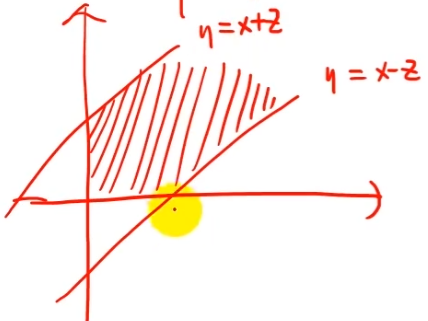
- =∬Dλ2e−λ(x+y)dxdy关于y=x对称2∫0+∞λe−λydy∫yy+zλe−λxdx
- e−λx→−λ1e−λx−2λ∫0+∞e−λy⋅e−λxx=yx=y+zdy
- =−2λ∫0+∞e−λy⋅(e−λy−λz−e−λy)dy提出e−λy−2λ∫0+∞e−2λy(e−λz−1)dy
- 提出z−2λ(e−λz−1)∫0+∞e−2λydy积分−2λe−2λy(e−λz−1)⋅e−2λy0+∞
- =(e−λz−1)⋅(−1)=1−e−λz.
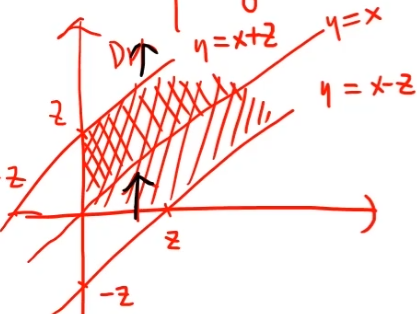
- Fz(z)={1−e−λz,z≥00,z≤0⇒fz(z)={λe−λz,0,z>0其他
- 从而选D
(11)
已知 x→0limx3(1+ax2)sinx−1=6, 则 a=
- x→0limx3(1+ax2)sinx−1(1+ax2)sinx=esinxln(1+ax2)x→0limx3esinxln(1+ax2)−1
- en−1∼ux→0limx3sinxln(1+ax2)
- sinu∼uln(1+n)∼ux→0limx3x⋅ax2=x→0limx3ax3=a.
(12)
已知 f(u,v) 具有二阶连续偏导数, 且 df∣(1,1)=3du+4dv, 若 y=f(cosx,1+x2), 则 dx2d2yx=0=
- df∣(1,1)=f1′(1,1)du+f2′(1,1)dv=3du+4dv
- f1′(1,1)=3,f1′(1,1)=4
- y=f(cosx,1+x2)
- 为了求二阶导所以求一阶导:
dxdy=f1′(cosx,1+x2)⋅(−sinx)+f2′(cosx,1+x2)⋅2x - 向题中条件靠近:
dx2d2y==0f11′′(cosx,1+x2)⋅(−sinx)2+f12′′(cosx,1+x2)⋅(−sinx)⋅2x
+f1′(cosx,1+x2)⋅(−cosx)
+=0f21′′(cosx,1+x2)⋅2x⋅(−sinx)+f22′′(cosx,1+x2)⋅(2x)2
+f2′(cosx⋅1+x2)⋅2- 求导乘法法则:右边不动,左边求导;左边不动,右边求导
- 将x=0代入得dx2dyx=0=f1′(1,1)⋅(−1)+f2′(1,1)⋅2=−3+4x2=5
(13)
已知 f(x)=1+x, 若 f(x)=2a0+n=1∑∞ancosnx,x∈[0,π], 则 n→∞limn2sina2n−1=
- 正弦级数与余弦级数 :设 f(x) 是周期为 2l 的周期函数. 记 C={xf(x)=21[f(x−)+f(x+)]}
- 当 f(x) 为奇函数时, f(x) 的傅里叶级数是只含正弦项的正弦级数
- f(x)=n=1∑∞bnsinlnπx(x∈C)
- 其中 bn=l2∫0lf(x)sinlnπx dx(n=1,2,⋯).
- 当 f(x) 为偶函数时, f(x) 的傅里叶级数是只含常数项和余弦项的余弦级数
- f(x)=2a0+n=1∑∞ancoslnπx(x∈C),
- 其中 an=l2∫0lf(x)coslnπx dx(n=0,1,2,⋯).
- 将l=πan=π2⋅∫0π(x+1)⋅πcosnπxdx
- an=π2∫0π(x+1)cosnxdx凑微分41⋅π2∫0π(x+1)d(sinnx)
- 分布0−0=0nπ2sinnx0π+nπ2∫0πxd(sinnx)分布nπ20−0=0xsinnx∣0π−∫0πsinnxdx
- 牛莱−sinnx→n1cosnxn2π2cosnx0πcosnπ=(−1)nn2π2[(−1)n−1]
- a2n−1=(2n−1)2π2⋅(−2)=−(2n−1)2π4
- n→∞limn2sina2n−1=n→∞limn2⋅sin(−(2n+1)2π4)sinn∼n−n→∞lim(2n−1)2π4n2
- =−n→∞lim(4n2−4n+1)π4n2=−π1.
- 相似题目
- 1991 年数一试题
- 将函数 f(x)=2+∣x∣(−1≤x≤1) 展开成以 2 为周期的傅里叶级数, 并由此求级数 n=1∑∞n21 的和.
- 1993 年数一试题
- 设函数 f(x)=πx+x2(−π<x<π) 的傅里叶级数展开式为 2a0+n=1∑∞(ancosnx+bnsinnx), 则其中系数 b3 的值为 .
- 1995 年数一试题
- 将函数 f(x)=x−1(0≤x≤2) 展开成周期为 4 的余弦级数.
- 2003 年数一试题
- 设 x2=n=0∑∞ancosnx(−π≤x≤π), 则 a2= .
- 2008 年数一试题
- 将函数 f(x)=1−x2(0≤x≤π) 展开成余弦级数, 并求 n=1∑∞n2(−1)n−1 的和.
- 2023 年数一试题
- 设 f(x) 是周期为 2 的周期函数,且 f(x)=1−x,x∈[0,1]. 若 f(x)=2a0+n=1∑∞ancosnπx, 则 n=1∑∞a2n=
- 狄利克雷定理
(14)
微分方程 y′=(x+y)21 满足条件 y(1)=0 的解为 .
- 令u=x+y,dxdu=1+dxdy则原结程y′=(x+y)21化为dxdy−1=u21。
- 移项dxdu=u21+u2分离变量1+u2u2du=dx
- 作差(1−1+u21)du=dx
- 积分u−arctanu=x+Cx=1,y=0,u=11−4π=1+C⇒C=−4π
- C=−4πu=x+yx+y−arctan(x+y)=x−4π⇒y−arctan(x+y)=−4π.
(15)
已知矩阵 A=(a+1aaa), 对于任意的 α=(x2x1),β=(y2y1), 都有 (αTAβ)2≤αTAα⋅βTAβ,则 a 的取值范围是
- αT=(x1,x2),βT=(y1,y2)
- (αTAβ)2≤αTAα⋅βTAβ分别计算三者的行列式
- αTAβ代入题中给出的行列式(x1,x2)(a+1aaa)(y1y2)
- 拆开,方便计算(x1,x2)[(aaaa)+(1000)](y1y2)
- A的行×B的列[ax1+ax2,ax1+ax2](y1y2)+(x1,0)(y1y2)
- A的行×B的列a(x1+x2)⋅(y1+y2)+x1y1
- 对称αTAα=(x1,x2)(a+1aaa)(x1x2)=a(x1+x2)(x1+x2)+x1x1
- 对称βTAβ=(y1,y2)(a+1aaa)(y1y2)=a(y1+y2)(y1+y2)+y1y1
- (αTAβ)2≤αTAα⋅βTAβ分别计算等号左右两个部分
- αTAα⋅βTAβ=[a(x1+x2)2+x12][a(y1+y2)2+y12]
- 乘法分配a(x1+x2)2y12+a(x1+x2)2⋅a(y1+y2)2+x12y12+x12⋅a(y1+y2)2
- (αTAβ)2=[a(x1+x2)⋅(y1+y2)+x1y1]2
- 完全平方a2(x1+x2)2(y1+y2)2+x12y12+2ax1y1(x1+x2)(y1+y2)
- (αTAβ)2≤αTAα⋅βTAβ
- a2(x1+x2)2(y1+y2)2+x12y12+2ax1y1(x1+x2)(y1+y2)
≤a(x1+x2)2y12+a(x1+x2)2⋅a(y1+y2)2+x12y12+x12⋅a(y1+y2)2 - a(x1+x2)2y12+ax12(y1+y2)2−2ax1y1(x1+x2)(y1+y2)≥0
- 完全平方a平方为正数[(x1+x2)y1−x1(y1+y2)]2≥0
- a≥0
(16)
设随机试验每次成功的概率为 p, 现进行 3 次独立重复试验, 在至少成功 1 次的条件下, 3 次试验全部成功的概率为 134, 则 p= .
- Cnk=k!(n−k)!n!,比如:C53=3!⋅2!5!=(3×2×1)⋅(2×1)5×4×3×2×1=10
- 二项分布X∼B(n,p),p{x=k}=Cnkpk(1−p)n−k
- P{x=3∣x⩾1}=P{x⩾1yP{x=3,x⩾1}=P{x⩾1}P{x=3}=1−P{x=0}C33p3
- =1−(1−p)3p3=134
- 交叉相乘13p3=4−4(1−p)3=4−4(1−3p+3p2−p3)
- 移项9p3+12p2−12p=0提取pp(3p2+4p−4)=0
- 因式分解p(p+2)(3p−2)=0⇒p=32.
(17)
(本题满分 10 分) 设 D={(x,y)∣1−y2≤x≤1,−1≤y≤1}, 求 ∬Dx2+y2xdxdy.
按极坐标算(2倍夜雨)
- ∬D=2∬D1=2(∬D3+∬D4)
- =2[∬D3cosθrdrdθ+∬D4cosθrdrdθ]
- =2∫4π2πdθ∫1sinθ1cosθ⋅rdr+2∫04πdθ∫1cosθ1cosθ⋅rdr
- 对r积分2⋅∫4π2πcosθ⋅2r21sinθ1dθ+2⋅∫04πcosθ⋅2r21cosθ1dθ
- 牛莱cosθdθ=d(sinθ)∫4π2πcosθ⋅(sin2θ1−1)dθ+∫04πsecθ−cosθ(cos2θ1−1)cosθdθ
- 对θ积分(−sinθ1−sinθ)4π2π+(ln∣secθ+tanθ∣−sinθ)∣04π
- =[(−1−1)−(−2−22)+[ln(2+1)−22]−[ln(1+0)−0]
- =−2+2+22+ln(2+1)−22−0
- =ln(2+1)−2+2
按极坐标算(2倍李艳芳)
- D 关于 x 轴对称,D1关于y=x 轴对称
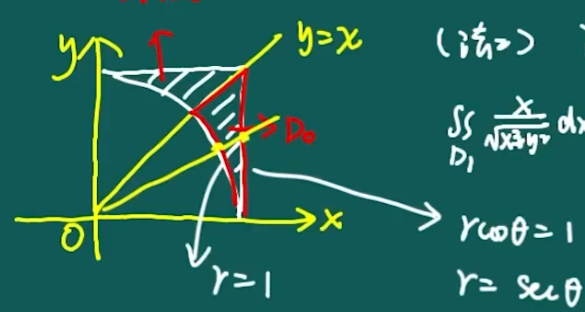
- ∬Dx2+y2xdxdy=∬D0x2+y2xdxdy+∬D0x2+y2ydxdy∬D1∣Dnx2+y2xdxdy=∬D0x2+y2x+ydxdy
- ∬D0x2+y2x+ydxdy=∬D0rr(cosθ+sinθ)⋅rdrdθ消去r∬D0(cosθ+sinθ)⋅rdrdθ
- 填入积分区域∫04π(cosθ+sinθ)dθ2sec2θ−1∫1secθrdr∫rdr=2r2∫04π(cosθ+sinθ)⋅2sec2θ−1dθ
- 提出系数21∫04π(cosθ+sinθ)(sec2θ−1)dθ
- 去括号21∫04π(secθ−cosθ+−sinθ=(cosθ)′cos2θsinθ−sinθ)dθ
- ∫secudu=ln∣secu+tanu∣+C21[ln(secθ+tanθ)−sinθ+cosθ1+cosθ]04π
- =21[ln(2+1)+2−2]
按直角坐标算(2倍)
- D 关于 x 轴对称,x2+y2x 关于 y 是偶函数。
- 记 D1 为 D 位于 x 轴上方的部分,则
∬Dx2+y2xdxdy=2∬D1x2+y2xdxdy
- 记 D1={(x,y)∣1−y2≤x≤1,0≤y≤1},则
- ∬Dx2+y2xdxdy对称性2∬D1x2+y2xdxdy代入上下限2∫01dy∫1−y21x2+y2xdx
- 统一∫01dy∫1−y21x2+y21d(x2+y2)=∫012x2+y2x=1−y2x=1dy
- 或∂x∂(x2+y2)=x2+y2x∫01x2+y2x=1−y2x=1dy
- =2∫01(1+y2−1)dy=2∫011+y2dy−2.
- 方法1,∫011+y2dy分部积分y1+y201−∫01y⋅1+y2ydy
- +1−12−∫011+y2y2+1−1dy
- 拆开变成两个2−∫011+y2dy+∫011+y21dy
- 绕回来了2−∫011+y2dy+ln(y+1+y2)01.
- 故 相加除以二∫011+y2dy=22+ln(1+2).
- 求∫011+y2dy−1
- y=tanu,(tanx)′=sec2x,tan4π=11+tan2α=sec2α∫04πsecu⋅sec2udu−1
- =∫04πsec3udu−1
- ∫04πsec3udu=∫04πsecu⋅d(tanu)=secu⋅tanu04π−∫04πtanu⋅secu⋅tanudu
- =2−∫04πtan2usecudutan2u+1=sec2u2−∫04π(sec2u−1)secudu
- =2−∫04πsec3udu+∫04πsecudu∫secudu=ln∣secu+tanu∣+C
- 2∫04πsec3udu=2+ln∣secu+tanu∣04π=2+ln(2+1)
- =21[ln(2+1)+2]−1
(18)
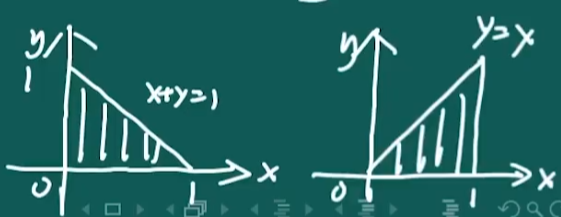
(本题满分 12 分) 设 f(x,y)=x3+y3−(x+y)2+3, 已知 z=f(x,y) 在 (1,1,1) 处的切平面方程为 T,T 与坐标平面所围成的有界区域在 xoy 面上的投影为 D 。
(1)求 T 的方程。
(2)求 f(x,y) 在 D 上的最大值和最小值。
求二元函数在有界闭区域上的最值
第二问(李艳芳版)
- 图示
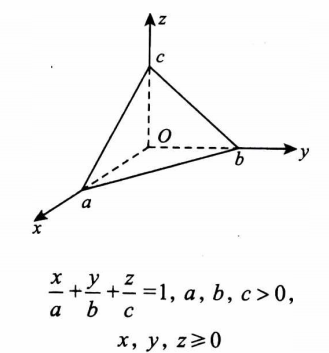
解题过程: - (II) 记 F(x,y)=z−f(x,y) 由题意 z=f(x,y) 即 F(x,y)=0。
- Fx(x0,y0)=−fx(x,y)=−3x2+2(xy)
- Fy(x0,y0)=−fy(x,y)=−3y2+2(xy)
- Fz(x0,y0)=1
- 代入 x=1,y=1,z=1 得 L 处的法向量为 (1,1,1)。
- T的点法式方程:
- F(x0,y0,z0)(x−x0)+Fy(x0,y0,z0)(y−y0)+Fz(x0,y0,z0)(z−z0)=0,
- 即 1⋅(x−1)+1⋅(y−1)+1⋅(z−7)=0
- ⇒x+y+z=3
- 图示
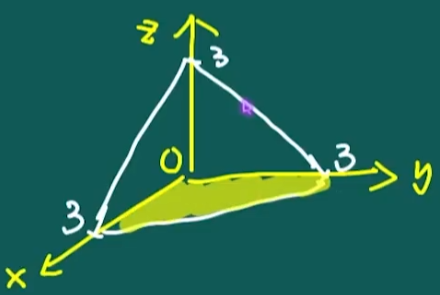
- (i) 先求 D 内部的驻点。
- {fx(x,y)=3x2−2(xy)=0fy(x,y)=3y2−2(xy)=0,得⇒3x2−3y2=0,从而(x+y)(x−y)=0
- 若 x=−y,则 (x,y) 不在 D 内部
- 故 x=y,代入 3x2−2(x+y)=0 得 3x2−4x=0
- ⇒x=0 或 x=34
- ⇒ 区域内部的一驻点为 (34,34)。
- f(34,34)=(34)3+(84)3−(38)2+3=27128−964+3=3−2764=2717
- 计算三个边界的值
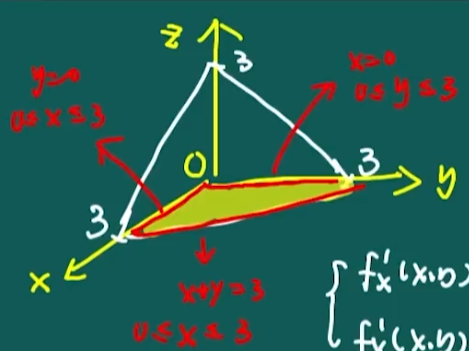
- 当y=0,0≤x≤3 时, f(x,0)=x3−x2+3=φ(x)
- φ′(x)=3x2−2x=x(3x−2)
- x=32 是 φ(x) 在 (0,3) 内的驻点。
- φ(32)=(32)3−(32)2+3=278−2712+3=2777
- φ(0)=3
- φ(3)=21
- x=0,0⩽y⩽3,最值情况与上述类似,是对称的
- 当x+y=3,0≤x≤3,
- f(x,y)=x3+(3−x)3−9+3=x3+(3−x)3−6=h(x)
- h′(x)=3x2−3(3−x)2−3⋅(9−6x+x2)18x−27=9(2x−3)
- x=23是h(x)在(0,3)内的驻点
- h(23)=(23)3+(3−23)3−6=827+827−6=43
- 两个端点 x=0,x=3
- h(0)=3
- h(3)=27−6=21
- 比较可得
- f(3,0)=f(0,3)=21
- f(34,34)=2717 是 f(x,y) 是区域 D上的最小值
高昆仑版
- 因为 f(x,y)=x3+y3−(x+y)2+3,所以
- ∂x∂f=3x2−2(x+y),∂y∂f=3y2−2(x+y)
- ∂x∂f(1,1)=−1,∂y∂f(1,1)=−1
- 法向量 n=(−1,−1,−1)。
- 切平面 T 的方程为 −1⋅(x−1)−1⋅(y−1)−1⋅(z−1)=0。
- 即 x+y+z=3。
- 图示

- (2) 由 (1) 知,切平面 T 与坐标面所围有界区域在 xOy 平面上的投影
D={(x,y)∣x≥0,y≥0,x+y≤3} - 令{∂x∂f=0,∂y∂f=0,即{3x2−2(x+y)=0,3y2−2(x+y)=0,
- 解得 D 内部的可疑点{x=34y=34
- 求边界上的点
- 当y=0时
- 当 (x,y)∈{(x,y)∣0≤x≤3,y=0} 时,f(x,0)=x3−x2+3, x∈[0,3]。
- 令dxd[f(x,0)]=3x2−2x=0,
- 得驻点 x=32。另有可疑点(端点)x=0 及 x=3。
- 当y=0时
- 当 (x,y)∈{(x,y)∣0≤y≤3,x=0} 时,由对称性,直接得驻点 y=32。另有可疑点(端点)y=0 及 y=3。
- x+y=3
- 当 (x,y)∈{(x,y)∣0≤x≤3,x+y=3} 时,
- f(x,3−x)=x3+(3−x)3−6,x∈[0,3]
- 令 dxd[f(x,3−x)]=3x2−3(3−x)2=0, 得 x=23.
- 综上,f(x,y) 在 D 上的可能最值点是 (0,0),(34,34),(32,0),(0,32),(3,0),(0,3),(23,23)。
- f(0,0)=3
- f(34,34)=2717
- f(32,0)=f(0,32)=2777
- f(3,0)=f(0,3)=21
- f(23,23)=43
- 所以 f(x,y) 在 D 上的最大值为 21,最小值为 2717。
(19)
(本题满分 12 分)
设函数 f(x) 具有 2 阶导数,且 f′(0)=f′(1),∣f′′(x)∣≤1 。证明
(1)当 x∈(0,1) 时, φ(x)∣f(x)−f(0)(1−x)−f(1)x∣≤一眼看出积分是1212x(1−x);
(2) ∫01f(x)dx−2f(0)+f(1)≤121
- ∣φ(x)∣≤2x(1−x)
- ∫01φ(x)dx=∫01f(x)dx−f(0)21∫01(1−x)dx−f(1)21∫01xdx
- =∫01f(x)dx−2f(0)+f(1)对应于第二问
- 分别写出 f(x) 在 x=0 与 x=1 处的一阶泰勒公式
- f(x)=f(0)+f′(0)x+2f′′(ξ1)x2,ξ1∈(0,x)×2
- f(x)=f(1)+f′(1)(x−1)+2f′′(ξ2)(x−1)2,ξ2∈(x,1)×(x−1)
- (2) 式 ×2 - (1) 式 ×(x−1) ,结合 f′(0)=f′(1) 可得
- f(x)=f(0)和f(1)xf(1)−(x−1)f(0)+2f′′(ξ2)(x−1)2⋅x−2f′′(ξ1)⋅x2(x−1)
- =xf(1)+(1−x)f(0)+提出公因式2x(x−1)[f′′(ξ2)⋅(x−1)−f′′(ξ1)x]
- 移项并整理,当 x∈(0,1) 时
∣f(x)−f(0)(1−x)−f(1)x∣=2x(x−1)[f′′(ξ2)(x−1)−f′′(ξ1)x]- 将x从绝对值中拿出2x(1−x)∣f′′(ξ2)(x−1)−f′′(ξ1)x∣
- 放缩∣a±b∣⩽∣a∣+∣b∣⩽2x(1−x)[∣f′′(ξ2)(x−1)∣+∣f′′(ξ1)x∣]
- =2x(1−x)继续从绝对值提出x[∣f′′(ξ2)∣⋅(1−x)+∣f′′(ξ1)∣x]
- ∣f′′(x)∣⩽1≤2x(1−x)[(1−x)+x](1−x)+x=12x(1−x)
- 第二问也可以拿分
- 记φ(x)=f(x)−f(0)(1−x)−f(1)x,由第一问可知:∣φ(x)∣≤2x(1−x)
- ∫01φ(x)dx三项分别积分∫01f(x)dx−f(0)∫01(1−x)dx−f(1)∫01xdx
- =∫01f(x)dx−2f(0)+f(1)
- 由
- 积分的绝对值小于等于绝对值的积分∫01φ(x)dx≤∫01∣φ(x)∣dx
- 以及 ∣φ(x)∣≤2x(1−x), 得∫01∣φ(x)∣dx≤∫012x(1−x)dx
- ∫01φ(x)dx=∫01f(x)dx−2f(0)+f(1)≤∫01∣φ(x)∣dx≤∫012x(1−x)dx
- =21∫01(x−x2)dx
- =21(2x2−3x3)01=121
(20)
(本题满分 12 分) 已知有向曲线 L 为球面 x2+y2+z2=2x 与平面 2x−z−1=0 的交线, 从 z轴正向往 z 轴负向看为逆时针方向, 计算曲线积分 ∮L(6xyz−yz2)dx+2x2zdy+xyzdz
夜雨版
- 取上侧方向,那么∫Γ(6xyz−yz2)dx+2x2z dy+xyz dz
- =∬Σdy dz dz dx dx dy∂x∂∂y∂∂z∂6xyz−yz22x2zxyz
- 按第一行展开∬Σ(xz−2x2)dy dz+(6xy−3yz)dz dx+(z2−2xz)dx dy
- 斯托克斯把曲线转换为平面,用高斯直接等于0
- 高斯只适用于曲面,不适用平面
- 选择将面投影到xOy
- z=2x−1,zx′=2,zy′=0∬ΣP⋅(−zx)+Q⋅(−zy)+R⋅1dxdy∬∑(xz−2x3⋅(−2)+(6xy−3yz)⋅(0)+(z2−2xz)⋅1)dxdy
- 整理∬∑(4x2−2xz)+(z2−2xz)dxdy
- 整理∬∑(2x−z)2dxdy
- 2x+z=1∬∑12dxdy
- 将z=2x−1代入x2+y2+z2=2x,得x2+y2+展开(2x−1)2−2x=0,
- 5x2−6x+y2+1=0.
- 配方椭圆标准形式5(x2−56x)+y2+1=0
- x2−56x+59和椭圆5(x−53)2+y2=54
- 同乘45a2(x−x0)2+b2(y−y0)2=1254(x−53)2+54y2=1
- 行如:椭圆面积:a2x2+b2y2=1、面积 πab
- D 是中心 (53,0)、长半轴长 54,短半轴长 254
- 则D 的面积为 π25454=554π=2545π
- 第二类曲面积分的计算方法三:合一投影法(这个方法用起来和上一个方法差不多)
- 若积分曲面 Σ 由方程 z=z(x,y) 给出, Σ 在 xOy 坐标面的投影为 Dxy, 函数 z(x,y) 在 Dxy 上有一阶连续偏导数, f(x,y,z) 在 Σ 上连续,
- 则有 ∬ΣPdydz+Qdxdz+Rdxdy=∬Σ[P⋅(−zx)+Q⋅(−zy)+R⋅1]dxdy
高昆仑版
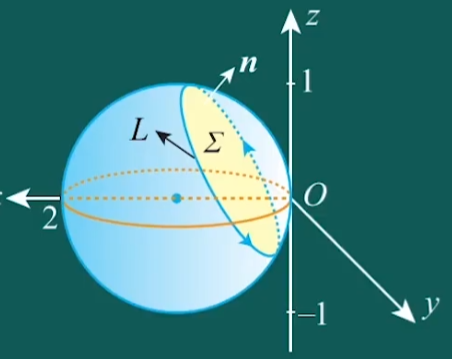
- 记曲线 L 在平面 2x−z−1=0 上所围部分为 Σ。
根据右手法则,取上侧。于是平面 Σ 的法向量 n=−{2,0,−1}={−2,0,1}。 - 由斯托克斯公式:空间线转空间面
I=∬Σcosα∂x∂Pcosβ∂y∂Qcosγ∂z∂RdScosα=5−2,cosβ=0,cosγ=51∬Σ5−2∂x∂6xyz−yz20∂y∂2x2z51∂z∂xyzdS- 51(−2xz−2x2−2xz+z2)∬5−2(xz−2x2)−0+51−2xz4xz−6xz+z2dS
- =∬Σ51(2x−z)2dS二代:2x−z=1一投影到xOy面:ds=1+zx′2+zy′2∬Dxy51⋅12⋅1+22+12=51+zx′2+zy′2dxdy
- =∬Dxy51⋅12⋅5dxdy=∬Dxy1dxdy=ADxy.
- 求投影椭圆的面积,由{x2+y2+z2=2x2x−z−1=0
- 消去 z,得 Dxy:x2+y2+(2x−1)2≤2x。
- 即 Dxy:5x2+y2−6x+1≤0。,配方Dxy:254(x−53)2+54y2≤1。
- ⇒ADxy椭圆面积=πabπ⋅52⋅52=554π.
李艳芳版

- 曲线L的方程是:{x2+y2+z2=2x2x−z−1=0,曲线L是封闭曲线L
- L 围成平面 2x−z−1=0 上的有界部分为 Σ、取上侧。记所求曲线积分为 I。
- L 的方向与 Σ 的方向符合右手法则(从上往下看),则由斯托克斯公式
- I=∮L(6xyz−yz2)dx+2x2zdy+xyzdz
- =∬Σdydzdzdxdxdy∂x∂∂y∂∂z∂6xyz−yz22x2zxyz
- 将第一行展开∬Σ(xz−2x2)dydz−(yz−2xy+2yz)dzdx+(z2−2xz)dxdy
- 合并整理∬Σ(xz−2x2)dydz+(6xy−3yz)dzdx+(z2−2xz)dxdy
- 提取公因式∬Σ(−x)(2x−z)dydz+3y(2x−z)dzdx+(−z)(2x−z)dxdy
- 代入2x−z=1∬Σ(−x)dydz+3ydzdx+(−z)dxdy
- 投影垂直于ZoX面∬z(−x)dydz+(−z)dxdy.
- 利用两类曲面积分之间的联系得
- ∬Σ(−x)dydz+(−z)dxdy转化为关于x,y的曲面积分
- 令:F(x,y,z) =z−2x+1∑:F(x,y,z)=0
- n 可取为 (Fx′,Fy′,Fz′)=(−2,0,1)
- cosα=5−2,cosβ=0,cosγ=51
- dydz=cosγcosαdxdy=−2dxdy
- 于是∬Σ(−x)dydz+(−z)dxdy
- dydz=cosγcosαdxdy=−2dxdy∬Σ[(−2)(−x)+(−z)]dxdy=∬Σ(2x−z)dxdy
- 2x−z=1∬Σdxdy=∬Ddxdy
- 将z=2x−1代入x2+y2+z2=2x,得x2+y2+(2x−1)2−2x=0,
- 5x2−6x+y2+1=0.
- 配方5(x2−56x)+y2+1=0
- 椭圆5(x−53)2+y2=54
- 254(x−53)2+54y2=1
- 行如:椭圆面积:a2x2+b2y2=1、面积 πab
- D 是中心 (53,0)、长半轴长 54,短半轴长 254
- 则D 的面积为 π25454=554π=2545π
- 1997 年数一试题
- 计算曲线积分∮C(z−y)dx+(x−z)dy+(x−y)dz,
其中 C 是曲线 {x2+y2=1,x→y+z=2, 从 z 轴正向往 z 轴负向看, C 的方向是顺时针的.
- 2001 年数一试题
- 计算 I=∮L(y2−z2)dx+(2z2−x2)dy+(3x2−y2)dz ,其中 L 是平面 x+y+z=2 与柱面 ∣x∣+∣y∣=1 的交线,从 z 轴正向看去, L 为逆时针方向.
- 2015 年数一试题
- 已知曲线 L 的方程为 {z=2−x2−y2,z=x, 起点为 A(0,2,0), 终点为 B(0,−2,0), 计算曲线积分 I=∫L(y+z)dx+(z2−x2+y)dy+x2y2 dz.
- 2022 年数一试题
- 已知 Σ 为曲面 4x2+y2+z2=1(x≥0,y≥0,z≥0) 的上侧, L 为 Σ 的边界曲线,其正向与 Σ 的正法向量满足右手法则,计算曲线积分I=∫L(yz2−cosz)dx+2xz2 dy+(2xyz+xsinz)dz.
(21)
(本题满分 12 分)
已知数列 {xn},{yn},{zn} 满足 x0=−1,y0=0,z0=2, 且 ⎩⎨⎧xn=−2xn−1+2zn−1yn=−2yn−1−2zn−1zn=−6xn−1−3yn−1+3zn−1, 记 αn=xnynzn,写出满足 αn=Aαn−1 的矩阵 A, 并求 An 及 xn,yn,zn(n=1,2,…).
- αn=Aαn−1正好对应xnynzn=Axn−1yn−1zn−1
- 由题中方程⎩⎨⎧xn=−2xn−1+2zn−1yn=−2yn−1−2zn−1zn=−6xn−1−3yn−1+3zn−1
- 提取系数矩阵xnynzn=A−20−60−2−32−23xn−1yn−1zn−1
- 得A=−2020−2−2−6−33
- 求An,要通过An=PΛnP−1求,所以要求矩阵A对应的特征向量和特征值
- 特征值组成对角矩阵
- 特征向量组成可逆矩阵
- 行初等变换求可逆矩阵的逆矩阵
- 求特征值:A−λE=−2−λ020−2−λ−2−6−33−λ
- r1+r2−2−λ−2−λ00−2−λ−2−6−33−λc2−c1−2−λ000−2−λ−2−633−λ
- 按第一行展开(−2−λ)[(−2−λ)(3−λ)−(−6)]
- =(−2−λ)[λ2−λ0−6+6]
- =(−2−λ)⋅λ(λ−1)
- 解得,λ1=0,λ2=1,λ3=−2
- 求每个特征值对应的特征向量:∣A−λ⋅E∣x=0
- λ=0,特征多项式∣A−0⋅E∣x=0
- −2020−2−2−6−33r3−3r1−2020−2−20−3−32,3两行成比例−101011000
- 令x3=1,则x=k11−11
- λ=1,特征多项式∣A−E∣x=0
- −3020−3−2−6−32r3−2r1−3020−3−20−3−2→30−2032000
- 设x3=3,则λ=k22−23
- λ=−2,特征多项式A+2Ex=0
- 00−600−32−25⟶600300010
- 由x3=0,设x2=2,则x=k3−120
- 将特征向量拼接成可逆矩阵
P=12−1−1−22130- P−1AP=Λ
- A=P∧P−1,Λ=01−2
- 由对角矩阵和可逆矩阵求n阶矩阵
An=P∧nP−1- 代入三个矩阵12−1−1−2213001−212−1−1−22130−1
- 通过化行最简矩阵求可逆矩阵12−1−1−22130−1
- 12−1100−1−22010130001r2+r1,r3−r112−1100001110011−101
- r3−r2,r2↔r312−1100010−2−11001110
- r1−2r2,r1+r310063−2010−2−11001110
- An=12−1−1−2213001(−2)n63−2−2−11110
- A的行乘B的列02−(−2)n0−22(−2)n03063−2−2−11110
- A的行乘B的列−4−(−2)n−2−(−2)n24+2⋅(−2)n2+2(−2)n−2−6−33
- 由递推关系求αn
αn=Aαn−1=A2αn−2=A3αn−3=Anα0- αn=Anα0xnynzn=Anx0y0z0=An−102
- 代入An−4+(−2)n−4−4−2(−2)n−46+6
2000 年数一试题
某试验性生产线每年一月份进行熟练工与非熟练工的人数统计,然后将 61 熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐。新、老非熟练工经过培训及实践至年终考核有 52 成为熟练工。设第 n 年一月份统计的熟练工和非熟练工所占百分比分别为 xn 和 yn, 记成向量 (ynxn).
(1) 求 (yn+1xn+1) 与 (ynxn) 的关系式并写成矩阵形式: (yn+1xn+1)=A(ynxn);
(2) 验证 η1=(14),η2=(1−1) 是 A 的两个线性无关的特征向量, 并求出相应的特征值;
(3) 当 (y1x1)=(2121) 时, 求 (yn+1xn+1).
1991 年数一试题
设3阶矩阵 A 的特征值为 λ1=1,λ2=2,λ3=3, 对应的特征向量依次为 ξ1=111,ξ2=124,ξ3=139, 又向量 β=113.
(1) 将 β 用 ξ1,ξ2,ξ3 线性表出; (2) 求 Anβ ( n 为自然数).
(22)
(本题满分 12 分)
设总体 X 服从 [0,θ] 上的均匀分布, 其中 θ∈(0,+∞) 为未知参数, X1,X2…….Xn 是来自总体 X 的简单随机样本, 记 X(n)=max{X1,X2…..Xn},Tc=cX(n).
(1)求 c, 使得 Tc 为 θ 的无偏估计量;
(2)记 h(c)=E(Tc−θ)2, 求 c 使得 h(c) 最小.
- 恒等变形:E(Tc)=θTc=cX(n)E(cX(n))=cE(X(n))=θ
- 求期望
- 先求分布函数
FX(n)(x)=P{X(n)≤x}X(n)=max{X1,X2,⋯,Xn}P{max{X1,x2,⋯,Xn}≤x}- =P{X1⩽x}⋯P{Xn⩽x}
- =⎩⎨⎧1,x>θ0,x<0(θ−0x−0)n=θnxn,0⩽x⩽θ
- 分布函数求导得概率密度
fX(n)(x)={θnnxn−1,0,0≤x≤θ 其他 - 何处求概率,何处算积分
E(X(n))=∫0θx⋅θnn⋅xn−1dx=θnn⋅∫0θxndx=θnn⋅n+1xn+10θ- =θnn⋅n+11⋅θn+1=n+1nθ
- 代入原式,得E(Tc)=cE(X(n))=θ
- c⋅n+1nθ=θ,得c=nn+1
- 恒等变形,得h(c)=E[(Tc−θ)2]Tc=cX(n)E[(cX(n)−θ)2]
- 完全平方E[c2X(n)2+θ2−2⋅cX(n)⋅θ]
- 提出系数c2E(X(n)2)+θ2−2c⋅θ⋅E(X(n))
- 定义法求:
E(X2)=∫0θx2⋅θnnxn−1dx=θnn⋅∫0θXn+1dx=θnn⋅n+2xn+20θ=n+2n⋅θ2
- E(X2)=n+2nθ2E(X)=n+1nθc2⋅n+2nθ2+θ2−2c⋅θ⋅n+1nθ
- 提出θ2θ2(n+2n⋅c2−1−2c⋅n+1n)
- x=−2ab二元函数求最小值−2⋅n+2n−2n+1n=n+1n+2