一、选择题 (本题共 8 小题, 每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有一项符合题目 要求,把所选项前的字母填在题后的括号内. )
(1) 下列曲线中有渐近线的是 ( ) (\quad) ( ) y = x + sin x y=x+\sin x y = x + sin x y = x 2 + sin x y=x^{2}+\sin x y = x 2 + sin x y = x + sin 1 x y=x+\sin \frac{1}{x} y = x + sin x 1 y = x 2 + sin 1 x y=x^{2}+\sin \frac{1}{x} y = x 2 + sin x 1
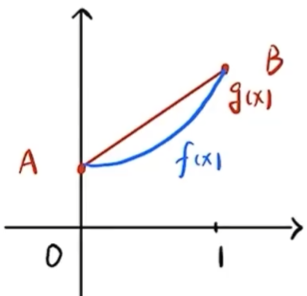
(1) 铅直渐近线 水平 再从X趋向于无穷时, 是否为常数 → \rightarrow → 斜 这四个选项显然没有铅直渐线和水平渐进线 那么就通过斜渐进线的公式 → \rightarrow → 分析四个函数的渐近线情况 判断选项 (A) y = x + sin x y = x + \sin x y = x + sin x 水平渐近线 计算 lim x → ∞ y = lim x → ∞ ( x + sin x ) = ∞ \displaystyle \lim_{x \to \infty} y = \lim_{x \to \infty} (x + \sin x) = \infty x → ∞ lim y = x → ∞ lim ( x + sin x ) = ∞ 不存在水平渐近线 并且是奇函数,则另一侧也没有水平渐近线 铅直渐近线 y = x + sin x y = x + \sin x y = x + sin x 斜渐近线 计算斜率 lim x → ∞ y x = lim x → ∞ ( 1 + sin x x ) = sin ∞ ∞ = 0 1 \displaystyle \lim_{x \to \infty} \frac{y}{x} = \lim_{x \to \infty} \left(1 + \frac{\sin x}{x}\right) \xlongequal[]{\frac{\sin{\infty}}{\infty}=0} 1 x → ∞ lim x y = x → ∞ lim ( 1 + x sin x ) ∞ s i n ∞ = 0 1 计算截距 lim x → ∞ ( y − x ) = lim x → ∞ sin x \displaystyle \lim_{x \to \infty} (y - x) = \lim_{x \to \infty} \sin x x → ∞ lim ( y − x ) = x → ∞ lim sin x 判断选项 (B) y = x 2 + sin x y = x^2 + \sin x y = x 2 + sin x 判断选项 (C) y = x + sin 1 x y = x + \sin \frac{1}{x} y = x + sin x 1 水平渐近线 铅直渐近线 间断点 x = 0 x = 0 x = 0 lim x → 0 y = lim x → 0 ( x + sin 1 x ) = x = 0 lim x → 0 sin 1 x ≠ ∞ \displaystyle \lim_{x \to 0} y =\lim _{x \rightarrow 0}\left(x+\sin \frac{1}{x}\right)\xlongequal[]{x=0} \lim_{x \to 0} \sin \frac{1}{x} \neq \infty x → 0 lim y = x → 0 lim ( x + sin x 1 ) x = 0 x → 0 lim sin x 1 = ∞ 斜渐近线 计算斜率 lim x → ∞ y x = lim x → ∞ x + sin 1 x x = 拆项 lim x → ∞ ( 1 + sin 1 x x ) = sin 1 ∞ ∞ = 0 1 + 0 = 1 \displaystyle \lim_{x \to \infty} \frac{y}{x} =\lim _{x \rightarrow \infty} \frac{x+\sin \frac{1}{x}}{x} \xlongequal[]{\text{拆项}}\lim _{x \rightarrow \infty}\left(1+\frac{\sin \frac{1}{x}}{x}\right)\xlongequal[]{\frac{\sin\frac{1}{\infty}}{\infty}=0}1+0=1 x → ∞ lim x y = x → ∞ lim x x + sin x 1 拆项 x → ∞ lim ( 1 + x sin x 1 ) ∞ s i n ∞ 1 = 0 1 + 0 = 1 计算截距 lim x → ∞ ( y − x ) = lim x → ∞ ( x + sin 1 x − x ) = lim x → ∞ sin 1 x = = sin 1 ∞ = sin 0 0 \displaystyle \lim_{x \to \infty} (y - x) =\lim _{x \rightarrow \infty}\left(x+\sin \frac{1}{x}-x\right)= \lim_{x \to \infty} \sin \frac{1}{x} =\xlongequal[]{\sin\frac{1}{\infty}=\sin0} 0 x → ∞ lim ( y − x ) = x → ∞ lim ( x + sin x 1 − x ) = x → ∞ lim sin x 1 = s i n ∞ 1 = s i n 0 0 判断选项 (D) y = x 2 + sin 1 x y = x^2 + \sin \frac{1}{x} y = x 2 + sin x 1 类似于选项 (B),无水平、铅直和斜渐近线y = x + sin 1 x y = x + \sin \frac{1}{x} y = x + sin x 1 y = x y = x y = x (2) 设函数 f ( x ) f(x) f ( x ) g ( x ) = f ( 0 ) ( 1 − x ) + f ( 1 ) x g(x)=f(0)(1-x)+f(1) x g ( x ) = f ( 0 ) ( 1 − x ) + f ( 1 ) x [ 0 , 1 ] [0,1] [ 0 , 1 ] ( ) (\quad) ( ) f ′ ( x ) ⩾ 0 f^{\prime}(x) \geqslant 0 f ′ ( x ) ⩾ 0 f ( x ) ⩾ g ( x ) f(x) \geqslant g(x) f ( x ) ⩾ g ( x ) f ′ ( x ) ⩾ 0 f^{\prime}(x) \geqslant 0 f ′ ( x ) ⩾ 0 f ( x ) ⩽ g ( x ) f(x) \leqslant g(x) f ( x ) ⩽ g ( x ) f ′ ′ ( x ) ⩾ 0 f^{\prime \prime}(x) \geqslant 0 f ′′ ( x ) ⩾ 0 f ( x ) ⩾ g ( x ) f(x) \geqslant g(x) f ( x ) ⩾ g ( x ) f ′ ′ ( x ) ⩾ 0 f^{\prime \prime}(x) \geqslant 0 f ′′ ( x ) ⩾ 0 f ( x ) ⩽ g ( x ) f(x) \leqslant g(x) f ( x ) ⩽ g ( x )
(2) 答 应选(D). 题中问的是, 当f ′ ( x ) ⩾ 0 f^{\prime}(x) \geqslant 0 f ′ ( x ) ⩾ 0 当f ′ ′ ( x ) ⩾ 0 f^{\prime \prime}(x) \geqslant 0 f ′′ ( x ) ⩾ 0 (3) 设 f ( x , y ) f(x, y) f ( x , y ) ∫ 0 1 d y ∫ − 1 − y 2 1 − y f ( x , y ) d x = ( ) \displaystyle \int_{0}^{1} \mathrm{~d} y \int_{-\sqrt{1-y^{2}}}^{1-y} f(x, y) \mathrm{d} x=(\quad) ∫ 0 1 d y ∫ − 1 − y 2 1 − y f ( x , y ) d x = ( ) ∫ 0 1 d x ∫ 0 x − 1 f ( x , y ) d y + ∫ − 1 0 d x ∫ 0 1 − x 2 f ( x , y ) d y \displaystyle \int_{0}^{1} \mathrm{~d} x \int_{0}^{x-1} f(x, y) \mathrm{d} y+\int_{-1}^{0} \mathrm{~d} x \int_{0}^{\sqrt{1-x^{2}}} f(x, y) \mathrm{d} y ∫ 0 1 d x ∫ 0 x − 1 f ( x , y ) d y + ∫ − 1 0 d x ∫ 0 1 − x 2 f ( x , y ) d y ∫ 0 1 d x ∫ 0 1 − x f ( x , y ) d y + ∫ − 1 0 d x ∫ − 1 − x 2 0 f ( x , y ) d y \displaystyle \int_{0}^{1} \mathrm{~d} x \int_{0}^{1-x} f(x, y) \mathrm{d} y+\int_{-1}^{0} \mathrm{~d} x \int_{-\sqrt{1-x^{2}}}^{0} f(x, y) \mathrm{d} y ∫ 0 1 d x ∫ 0 1 − x f ( x , y ) d y + ∫ − 1 0 d x ∫ − 1 − x 2 0 f ( x , y ) d y ∫ 0 π 2 d θ ∫ 0 1 cos θ + sin θ f ( r cos θ , r sin θ ) d r + ∫ π 2 π d θ ∫ 0 1 f ( r cos θ , r sin θ ) d r \displaystyle \int_{0}^{\frac{\pi}{2}} \mathrm{~d} \theta \int_{0}^{\frac{1}{\cos \theta+\sin \theta}} f(r \cos \theta, r \sin \theta) \mathrm{d} r+\int_{\frac{\pi}{2}}^{\pi} \mathrm{d} \theta \int_{0}^{1} f(r \cos \theta, r \sin \theta) \mathrm{d} r ∫ 0 2 π d θ ∫ 0 c o s θ + s i n θ 1 f ( r cos θ , r sin θ ) d r + ∫ 2 π π d θ ∫ 0 1 f ( r cos θ , r sin θ ) d r ∫ 0 π 2 d θ ∫ 0 cos θ + sin θ f ( r cos θ , r sin θ ) r d r + ∫ π 2 π d θ ∫ 0 1 f ( r cos θ , r sin θ ) r d r \displaystyle \int_{0}^{\frac{\pi}{2}} \mathrm{~d} \theta \int_{0}^{\cos \theta+\sin \theta} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r+\int_{\frac{\pi}{2}}^{\pi} \mathrm{d} \theta \int_{0}^{1} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r ∫ 0 2 π d θ ∫ 0 c o s θ + s i n θ f ( r cos θ , r sin θ ) r d r + ∫ 2 π π d θ ∫ 0 1 f ( r cos θ , r sin θ ) r d r
(3) 答 应选(D). AB选项是交换x和y的积分次序− 1 ⩽ x ⩽ 0 , 0 ⩽ y ⩽ 1 − x 2 \displaystyle \begin{array}{ll}-1 \leqslant x \leqslant 0, & 0 \leqslant y \leqslant \sqrt{1-x^2}\end{array} − 1 ⩽ x ⩽ 0 , 0 ⩽ y ⩽ 1 − x 2 0 ⩽ x ⩽ 1 , 0 ⩽ y ⩽ 1 − x 0 \leqslant x \leqslant 1, 0 \leqslant y \leqslant 1-x 0 ⩽ x ⩽ 1 , 0 ⩽ y ⩽ 1 − x 在直角坐标系下,原式 = ∫ − 1 0 d x ∫ 0 1 − x f ( x , y ) d y + ∫ 0 1 d x ∫ 0 1 − x f ( x , y ) d y \displaystyle =\int_{-1}^0 \mathrm{~d} x \int_0^{\sqrt{1-x}} f(x, y) \mathrm{d} y+\int_0^1 \mathrm{~d} x \int_0^{1-x} f(x, y) \mathrm{d} y = ∫ − 1 0 d x ∫ 0 1 − x f ( x , y ) d y + ∫ 0 1 d x ∫ 0 1 − x f ( x , y ) d y CD选项是将直角坐标系化为极坐标系在极坐标系下,= ∫ 0 π 2 d θ ∫ 0 1 cos θ + sin θ f ( r cos θ , r sin θ ) r d r + ∫ π 2 π d θ ∫ 0 1 f ( r cos θ , r sin θ ) r d r \displaystyle =\int_0^{\frac{\pi}{2}} \mathrm{~d} \theta \int_0^{\frac{1}{\cos \theta+\sin \theta}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r+\int_{\frac{\pi}{2}}^\pi d \theta \int_0^1 f(r \cos \theta, r \sin \theta) r \mathrm{~d} r = ∫ 0 2 π d θ ∫ 0 c o s θ + s i n θ 1 f ( r cos θ , r sin θ ) r d r + ∫ 2 π π d θ ∫ 0 1 f ( r cos θ , r sin θ ) r d r 故应该选(D). (4) 若 ∫ − π π ( x − a 1 cos x − b 1 sin x ) 2 d x = min a , b ∈ R { ∫ − π π ( x − a cos x − b sin x ) 2 d x } \displaystyle \int_{-\pi}^{\pi}\left(x-a_{1} \cos x-b_{1} \sin x\right)^{2} \mathrm{~d} x=\min _{a, b \in \mathbf{R}}\left\{\int_{-\pi}^{\pi}(x-a \cos x-b \sin x)^{2} \mathrm{~d} x\right\} ∫ − π π ( x − a 1 cos x − b 1 sin x ) 2 d x = a , b ∈ R min { ∫ − π π ( x − a cos x − b sin x ) 2 d x } a 1 cos x + b 1 sin x = ( a_{1} \cos x+b_{1} \sin x=(\quad a 1 cos x + b 1 sin x = ( 2 sin x 2 \sin x 2 sin x 2 cos x 2 \cos x 2 cos x 2 π sin x 2 \pi \sin x 2 π sin x 2 π cos x 2 \pi \cos x 2 π cos x
(4) 答 应选(A). ∫ − π π ( x − a cos x − b sin x ) 2 d x \displaystyle \begin{aligned} \int_{-\pi}^\pi(x-a \cos x-b \sin x)^2 \mathrm{~d} x & \end{aligned} ∫ − π π ( x − a cos x − b sin x ) 2 d x = 完全平方 ∫ − π π ( x 2 + a 2 cos 2 x + b 2 sin 2 x − 2 a x cos x − 2 b x sin x + 2 a b sin x cos x ) d x \displaystyle \begin{aligned}\xlongequal[]{\text{完全平方}}\int_{-\pi}^\pi\left(x^2+a^2 \cos ^2 x+b^2 \sin ^2 x-2 a x \cos x-2 b x \sin x+2 a b \sin x \cos x\right) \mathrm{d} x\end{aligned} 完全平方 ∫ − π π ( x 2 + a 2 cos 2 x + b 2 sin 2 x − 2 a x cos x − 2 b x sin x + 2 ab sin x cos x ) d x = 奇函数为 0 对称性 2 ∫ 0 π x 2 d x + 2 ∫ 0 π ( a 2 cos 2 x + b 2 sin 2 x − 2 b x sin x ) d x ⏟ 分成两部分计算 \displaystyle \begin{aligned} \xlongequal[\text{奇函数为}0]{\text { 对称性 }} 2 \int_0^\pi x^2 \mathrm{~d} x+\underbrace{2 \int_0^\pi\left(a^2 \cos ^2 x+b^2 \sin ^2 x-2 b x \sin x\right) \mathrm{d} x}_{\text{分成两部分计算}} \end{aligned} 对称性 奇函数为 0 2 ∫ 0 π x 2 d x + 分成两部分计算 2 ∫ 0 π ( a 2 cos 2 x + b 2 sin 2 x − 2 b x sin x ) d x 2 ∫ 0 π ( a 2 cos 2 x + b 2 sin 2 x ) d x \displaystyle 2 \int_0^\pi\left(a^2 \cos ^2 x+b^2 \sin ^2 x\right) d x 2 ∫ 0 π ( a 2 cos 2 x + b 2 sin 2 x ) d x = ∫ 0 π sin 2 x d x = 2 ∫ 0 π 2 sin 2 x d x ∫ 0 π cos 2 x d x = 2 ∫ 0 π 3 cos 2 x d x 4 ( a 2 + b 2 ) ∫ 0 π 2 cos 2 x d x \displaystyle \xlongequal[\int_0^\pi \sin ^2 x d x=2 \int_0^{\frac{\pi}{2}} \sin ^2 x d x]{\int_0^\pi \cos ^2 x d x=2 \int_0^{\frac{\pi}{3}} \cos ^2 x d x}4\left(a^2+b^2\right) \int_0^{\frac{\pi}{2}} \cos ^2 x d x ∫ 0 π c o s 2 x d x = 2 ∫ 0 3 π c o s 2 x d x ∫ 0 π s i n 2 x d x = 2 ∫ 0 2 π s i n 2 x d x 4 ( a 2 + b 2 ) ∫ 0 2 π cos 2 x d x = ∫ 0 π 2 cos 2 x d x = 1 2 × π 2 4 ( a 2 + b 2 ) ⋅ 1 2 × π 2 \displaystyle \xlongequal[]{\int_0^{\frac{\pi}{2}} \cos ^2 x d x=\frac{1}{2} \times \frac{\pi}{2}}4\left(a^2+b^2\right) \cdot \frac{1}{2} \times \frac{\pi}{2} ∫ 0 2 π c o s 2 x d x = 2 1 × 2 π 4 ( a 2 + b 2 ) ⋅ 2 1 × 2 π ∫ 0 π x sin x d x = − ∫ 0 π x d ( cos x ) \displaystyle \int_0^\pi x \sin x d x=-\int_0^\pi x d(\cos x) ∫ 0 π x sin x d x = − ∫ 0 π x d ( cos x ) = − [ x cos x ∣ 0 π − ∫ 0 π cos x d x ] \displaystyle \begin{aligned} & =-\left[\left.x \cos x\right|_0 ^\pi-\int_0^\pi \cos x d x\right] \end{aligned} = − [ x cos x ∣ 0 π − ∫ 0 π cos x d x ] = π \displaystyle \begin{aligned} =\pi \end{aligned} = π = 2 π 3 3 + 4 ( a 2 + b 2 ) ⋅ 1 2 × π 2 − 4 b π \displaystyle \begin{aligned}=\frac{2 \pi^3}{3}+4\left(a^2+b^2\right) \cdot \frac{1}{2} \times \frac{\pi}{2}-4b \pi\end{aligned} = 3 2 π 3 + 4 ( a 2 + b 2 ) ⋅ 2 1 × 2 π − 4 bπ = 2 3 π 3 + ( a 2 + b 2 − 4 b ) π . \displaystyle \begin{aligned} =\frac{2}{3} \pi^3+\left(a^2+b^2-4 b\right) \pi . \end{aligned} = 3 2 π 3 + ( a 2 + b 2 − 4 b ) π . 本题相当于求函数 a 2 + b 2 − 4 b a^2+b^2-4 b a 2 + b 2 − 4 b a = 0 , b = 2 a=0, b=2 a = 0 , b = 2 ∫ − π π ( x − a cos x − b sin x ) 2 d x \displaystyle \int_{-\pi}^\pi(x-a \cos x-b \sin x)^2 \mathrm{~d} x ∫ − π π ( x − a cos x − b sin x ) 2 d x (5) 行列式 ∣ 0 a b 0 a 0 0 b 0 c d 0 c 0 0 d ∣ = ( \displaystyle \left|\begin{array}{llll}0 & a & b & 0 \\ a & 0 & 0 & b \\ 0 & c & d & 0 \\ c & 0 & 0 & d\end{array}\right|=(\quad 0 a 0 c a 0 c 0 b 0 d 0 0 b 0 d = ( ( a d − b c ) 2 (a d-b c)^{2} ( a d − b c ) 2 − ( a d − b c ) 2 -(a d-b c)^{2} − ( a d − b c ) 2 a 2 d 2 − b 2 c 2 a^{2} d^{2}-b^{2} c^{2} a 2 d 2 − b 2 c 2
(5) 直接按行或按列展开,而不是去两两交换某一行或某一列 ∣ 0 a b 0 a 0 0 b 0 c d 0 c 0 0 d ∣ = 按第一列展开 注意正负号 a ( − 1 ) 2 + 1 ∣ a b 0 c d 0 0 0 d ∣ ⏟ 按第三列展开 + c ( − 1 ) 4 + 1 ∣ a b 0 0 0 b c d 0 ∣ ⏟ 按第二行展开 \displaystyle \left|\begin{array}{llll}0 & a & b & 0 \\ a & 0 & 0 & b \\ 0 & c & d & 0 \\ c & 0 & 0 & d\end{array}\right|\xlongequal[\text{按第一列展开}]{\text{注意正负号}}\underbrace{a(-1)^{2+1}\left|\begin{array}{lll}a & b & 0 \\ c & d & 0 \\ 0 & 0 & d\end{array}\right|}_{\text{按第三列展开}}+\underbrace{c(-1)^{4+1}\left|\begin{array}{lll}a & b & 0 \\ 0 & 0 & b \\ c & d & 0\end{array}\right|}_{\text{按第二行展开}} 0 a 0 c a 0 c 0 b 0 d 0 0 b 0 d 注意正负号 按第一列展开 按第三列展开 a ( − 1 ) 2 + 1 a c 0 b d 0 0 0 d + 按第二行展开 c ( − 1 ) 4 + 1 a 0 c b 0 d 0 b 0 − a d ∣ a b c d ∣ + b c ∣ a b c d ∣ = − ( a d − b c ) ∣ a b c d ∣ = − ( a d − b c ) 2 \displaystyle -a d\left|\begin{array}{ll}a & b \\c & d\end{array}\right|+b c\left|\begin{array}{ll}a & b \\c & d\end{array}\right|=-(a d-b c)\left|\begin{array}{ll}a & b \\c & d\end{array}\right|=-(a d-b c)^2 − a d a c b d + b c a c b d = − ( a d − b c ) a c b d = − ( a d − b c ) 2 ∣ 0 a b 0 a 0 0 b 0 c d 0 c 0 0 d ∣ = r 1 → r 4 − ∣ c 0 0 d a 0 0 b 0 c d 0 0 a b 0 ∣ = c 2 → c 1 ∣ c d 0 0 a b 0 0 0 0 d c 0 0 b a ∣ = ( b c − a d ) ( a d − b c ) = − ( a d − b c ) 2 . \displaystyle \left|\begin{array}{llll}0 & a & b & 0 \\a & 0 & 0 & b \\0 & c & d & 0 \\c & 0 & 0 & d\end{array}\right| \stackrel{r_1 \rightarrow r_4}{=}-\left|\begin{array}{llll}c & 0 & 0 & d \\a & 0 & 0 & b \\0 & c & d & 0 \\0 & a & b & 0\end{array}\right| \stackrel{c_2 \rightarrow c_1}{=}\left|\begin{array}{llll}c & d & 0 & 0 \\a & b & 0 & 0 \\0 & 0 & d & c \\0 & 0 & b & a\end{array}\right|=(b c-a d)(a d-b c)=-(a d-b c)^2 . 0 a 0 c a 0 c 0 b 0 d 0 0 b 0 d = r 1 → r 4 − c a 0 0 0 0 c a 0 0 d b d b 0 0 = c 2 → c 1 c a 0 0 d b 0 0 0 0 d b 0 0 c a = ( b c − a d ) ( a d − b c ) = − ( a d − b c ) 2 . ∣ 0 a b 0 a 0 0 b 0 c d 0 c 0 0 d ∣ = a ( − 1 ) 2 + 1 ∣ a b 0 c d 0 0 0 d ∣ + c ( − 1 ) 4 + 1 ∣ a b 0 0 0 b c d 0 ∣ \displaystyle \begin{aligned} \left|\begin{array}{llll}0 & a & b & 0 \\a & 0 & 0 & b \\0 & c & d & 0 \\c & 0 & 0 & d\end{array}\right| & =a(-1)^{2+1}\left|\begin{array}{lll}a & b & 0 \\c & d & 0 \\0 & 0 & d\end{array}\right|+c(-1)^{4+1}\left|\begin{array}{lll}a & b & 0 \\0 & 0 & b \\c & d & 0\end{array}\right| \end{aligned} 0 a 0 c a 0 c 0 b 0 d 0 0 b 0 d = a ( − 1 ) 2 + 1 a c 0 b d 0 0 0 d + c ( − 1 ) 4 + 1 a 0 c b 0 d 0 b 0 = − a d ∣ a b c d ∣ + b c ∣ a b c d ∣ = − ( a d − b c ) ∣ a b c d ∣ = − ( a d − b c ) 2 . \displaystyle \begin{aligned} =-a d\left|\begin{array}{ll}a & b \\c & d\end{array}\right|+b c\left|\begin{array}{ll}a & b \\c & d\end{array}\right|=-(a d-b c)\left|\begin{array}{ll}a & b \\c & d\end{array}\right|=-(a d-b c)^2 . \end{aligned} = − a d a c b d + b c a c b d = − ( a d − b c ) a c b d = − ( a d − b c ) 2 . A \boldsymbol{A} A B \boldsymbol{B} B m m m n n n ∣ A ∗ O B ∣ = ∣ A O ∗ B ∣ = ∣ A ∣ ∣ B ∣ , ∣ O A B ∗ ∣ = ∣ ∗ A B O ∣ = ( − 1 ) m n ∣ A ∣ ∣ B ∣ . \displaystyle \left|\begin{array}{ll}\boldsymbol{A} & * \\\boldsymbol{O} & \boldsymbol{B}\end{array}\right|=\left|\begin{array}{cc}\boldsymbol{A} & \boldsymbol{O} \\* & \boldsymbol{B}\end{array}\right|=|\boldsymbol{A}||\boldsymbol{B}|,\left|\begin{array}{cc}\boldsymbol{O} & \boldsymbol{A} \\\boldsymbol{B} & *\end{array}\right|=\left|\begin{array}{cc}* & \boldsymbol{A} \\\boldsymbol{B} & \boldsymbol{O}\end{array}\right|=(-1)^{m n}|\boldsymbol{A}||\boldsymbol{B}| . A O ∗ B = A ∗ O B = ∣ A ∣∣ B ∣ , O B A ∗ = ∗ B A O = ( − 1 ) mn ∣ A ∣∣ B ∣. (6) 设 α 1 , α 2 , α 3 \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3} α 1 , α 2 , α 3 k , l k, l k , l α 1 + k α 3 , α 2 + l α 3 \boldsymbol{\alpha}_{1}+k \boldsymbol{\alpha}_{3}, \boldsymbol{\alpha}_{2}+l \boldsymbol{\alpha}_{3} α 1 + k α 3 , α 2 + l α 3 α 1 \boldsymbol{\alpha}_{1} α 1 α 2 , α 3 \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3} α 2 , α 3
(6) 答 应选 (A).α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 λ 1 ( α 1 + k α 3 ) + λ 2 ( α 2 + l α 3 ) = 0 \lambda_1\left(\boldsymbol{\alpha}_1+k \boldsymbol{\alpha}_3\right)+\lambda_2\left(\boldsymbol{\alpha}_2+l \boldsymbol{\alpha}_3\right)=\mathbf{0} λ 1 ( α 1 + k α 3 ) + λ 2 ( α 2 + l α 3 ) = 0 λ 1 α 1 + λ 2 α 2 + ( k λ 1 + l λ 2 ) α 3 = 0 ⇒ λ 1 = λ 2 = k λ 1 + l λ 2 = 0 , \lambda_1 \boldsymbol{\alpha}_1+\lambda_2 \boldsymbol{\alpha}_2+\left(k \lambda_1+l \lambda_2\right) \boldsymbol{\alpha}_3=0 \Rightarrow \lambda_1=\lambda_2=k \lambda_1+l \lambda_2=0, λ 1 α 1 + λ 2 α 2 + ( k λ 1 + l λ 2 ) α 3 = 0 ⇒ λ 1 = λ 2 = k λ 1 + l λ 2 = 0 , α 1 + k α 3 , α 2 + l α 3 \boldsymbol{\alpha}_1+k \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_2+l \boldsymbol{\alpha}_3 α 1 + k α 3 , α 2 + l α 3 α 1 + k α 3 , α 2 + l α 3 \boldsymbol{\alpha}_1+k \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_2+l \boldsymbol{\alpha}_3 α 1 + k α 3 , α 2 + l α 3 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 α 1 = ( 1 0 0 ) , α 2 = ( 0 1 0 ) , α 3 = ( 0 0 0 ) . \displaystyle \boldsymbol{\alpha}_1=\left(\begin{array}{l}1 \\0 \\0\end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{l}0 \\1 \\0\end{array}\right), \boldsymbol{\alpha}_3=\left(\begin{array}{l}0 \\0 \\0\end{array}\right) . α 1 = 1 0 0 , α 2 = 0 1 0 , α 3 = 0 0 0 . α 1 + k α 3 , α 2 + l α 3 \boldsymbol{\alpha}_1+k \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_2+l \boldsymbol{\alpha}_3 α 1 + k α 3 , α 2 + l α 3 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 α 1 + k α 3 , α 2 + l α 3 \boldsymbol{\alpha}_1+k \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_2+l \boldsymbol{\alpha}_3 α 1 + k α 3 , α 2 + l α 3 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 k = l = 0 k=l=0 k = l = 0 α 1 , α 2 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2 α 1 , α 2 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 (7) 设随机事件 A A A B B B P ( B ) = 0.5 , P ( A − B ) = 0.3 P(B)=0.5, P(A-B)=0.3 P ( B ) = 0.5 , P ( A − B ) = 0.3 P ( B − A ) = ( ) P(B-A)=(\quad) P ( B − A ) = ( )
(7) 解
由随机事件 A A A B B B P ( A B ) = P ( A ) P ( B ) P(A B)=P(A) P(B) P ( A B ) = P ( A ) P ( B ) 先写出P ( A − B ) P(A-B) P ( A − B ) P ( B − A ) P(B-A) P ( B − A ) P ( A − B ) = P ( A ) − P ( A B ) = P ( A ∣ B ˉ ) = A 与 B 独立 P ( A ) − P ( A ) P ( B ) P(A-B) = P(A) - P(AB) =P(A \mid \bar{B})\xlongequal[]{A\text{与}B\text{独立}} P(A) - P(A)P(B) P ( A − B ) = P ( A ) − P ( A B ) = P ( A ∣ B ˉ ) A 与 B 独立 P ( A ) − P ( A ) P ( B ) 代入 P ( A − B ) = 0.3 P(A-B) = 0.3 P ( A − B ) = 0.3 P ( B ) = 0.5 P(B) = 0.5 P ( B ) = 0.5 解得 P ( A ) = 0.6 P(A) = 0.6 P ( A ) = 0.6 P ( B − A ) = P ( B ) − P ( A B ) = P ( B ∣ A ˉ ) = 独立性 P ( B ) − P ( A ) P ( B ) P(B-A) = P(B) - P(AB) =P (B |\bar{A})\xlongequal[]{\text{独立性}} P(B) - P(A)P(B) P ( B − A ) = P ( B ) − P ( A B ) = P ( B ∣ A ˉ ) 独立性 P ( B ) − P ( A ) P ( B ) 计算结果:代入 P ( B ) = 0.5 P(B) = 0.5 P ( B ) = 0.5 P ( A ) = 0.6 P(A) = 0.6 P ( A ) = 0.6 得 P ( B − A ) = 0.5 − 0.5 × 0.6 = 0.2 P(B-A) = 0.5 - 0.5 \times 0.6 = 0.2 P ( B − A ) = 0.5 − 0.5 × 0.6 = 0.2 (8) 设连续型随机变量 X 1 X_{1} X 1 X 2 X_{2} X 2 X 1 X_{1} X 1 X 2 X_{2} X 2 f 1 ( x ) f_{1}(x) f 1 ( x ) f 2 ( x ) f_{2}(x) f 2 ( x ) Y 1 Y_{1} Y 1 f Y 1 ( y ) = 1 2 [ f 1 ( y ) + f 2 ( y ) ] f_{Y_{1}}(y)=\frac{1}{2}\left[f_{1}(y)+f_{2}(y)\right] f Y 1 ( y ) = 2 1 [ f 1 ( y ) + f 2 ( y ) ] Y 2 = 1 2 ( X 1 + X 2 ) Y_{2}=\frac{1}{2}\left(X_{1}+X_{2}\right) Y 2 = 2 1 ( X 1 + X 2 ) ( ) (\quad) ( ) E ( Y 1 ) > E ( Y 2 ) , D ( Y 1 ) > D ( Y 2 ) E\left(Y_{1}\right)>E\left(Y_{2}\right), D\left(Y_{1}\right)>D\left(Y_{2}\right) E ( Y 1 ) > E ( Y 2 ) , D ( Y 1 ) > D ( Y 2 ) E ( Y 1 ) = E ( Y 2 ) , D ( Y 1 ) = D ( Y 2 ) E\left(Y_{1}\right)=E\left(Y_{2}\right), D\left(Y_{1}\right)=D\left(Y_{2}\right) E ( Y 1 ) = E ( Y 2 ) , D ( Y 1 ) = D ( Y 2 ) E ( Y 1 ) = E ( Y 2 ) , D ( Y 1 ) < D ( Y 2 ) E\left(Y_{1}\right)=E\left(Y_{2}\right), D\left(Y_{1}\right)<D\left(Y_{2}\right) E ( Y 1 ) = E ( Y 2 ) , D ( Y 1 ) < D ( Y 2 ) E ( Y 1 ) = E ( Y 2 ) , D ( Y 1 ) > D ( Y 2 ) E\left(Y_{1}\right)=E\left(Y_{2}\right), D\left(Y_{1}\right)>D\left(Y_{2}\right) E ( Y 1 ) = E ( Y 2 ) , D ( Y 1 ) > D ( Y 2 )
(8) 答 应选(D). E Y 1 = 1 2 ∫ − ∞ + ∞ y [ f 1 ( y ) + f 2 ( y ) ] d y = 1 2 ( E X 1 + E X 2 ) = E Y 2 , \displaystyle \begin{aligned} E Y_1=\frac{1}{2} \int_{-\infty}^{+\infty} y\left[f_1(y)+f_2(y)\right] \mathrm{d} y=\frac{1}{2}\left(E X_1+E X_2\right)=E Y_2, \end{aligned} E Y 1 = 2 1 ∫ − ∞ + ∞ y [ f 1 ( y ) + f 2 ( y ) ] d y = 2 1 ( E X 1 + E X 2 ) = E Y 2 , E ( Y 1 2 ) = 1 2 ∫ − ∞ + ∞ y 2 [ f 1 ( y ) + f 2 ( y ) ] d y = 1 2 E ( X 1 2 ) + 1 2 E ( X 2 2 ) , \displaystyle \begin{aligned} E\left(Y_1^2\right)=\frac{1}{2} \int_{-\infty}^{+\infty} y^2\left[f_1(y)+f_2(y)\right] \mathrm{d} y=\frac{1}{2} E\left(X_1^2\right)+\frac{1}{2} E\left(X_2^2\right), \end{aligned} E ( Y 1 2 ) = 2 1 ∫ − ∞ + ∞ y 2 [ f 1 ( y ) + f 2 ( y ) ] d y = 2 1 E ( X 1 2 ) + 2 1 E ( X 2 2 ) , D Y 1 = E ( Y 1 2 ) − ( E Y 1 ) 2 = 1 2 E ( X 1 2 ) + 1 2 E ( X 2 2 ) − 1 4 ( E X 1 ) 2 − 1 4 ( E X 2 ) 2 − 1 2 E X 1 E X 2 \displaystyle \begin{aligned} D Y_1=E\left(Y_1^2\right)-\left(E Y_1\right)^2=\frac{1}{2} E\left(X_1^2\right)+\frac{1}{2} E\left(X_2^2\right)-\frac{1}{4}\left(E X_1\right)^2-\frac{1}{4}\left(E X_2\right)^2-\frac{1}{2} E X_1 E X_2 \end{aligned} D Y 1 = E ( Y 1 2 ) − ( E Y 1 ) 2 = 2 1 E ( X 1 2 ) + 2 1 E ( X 2 2 ) − 4 1 ( E X 1 ) 2 − 4 1 ( E X 2 ) 2 − 2 1 E X 1 E X 2 = 1 4 D X 1 + 1 4 D X 2 + 1 4 E [ ( X 1 − X 2 ) 2 ] > 1 4 D X 1 + 1 4 D X 2 = D Y 2 , \displaystyle \begin{aligned} =\frac{1}{4} D X_1+\frac{1}{4} D X_2+\frac{1}{4} E\left[\left(X_1-X_2\right)^2\right]>\frac{1}{4} D X_1+\frac{1}{4} D X_2=D Y_2, \end{aligned} = 4 1 D X 1 + 4 1 D X 2 + 4 1 E [ ( X 1 − X 2 ) 2 ] > 4 1 D X 1 + 4 1 D X 2 = D Y 2 , 二、填空题 (本题共 6 小题,每小题 4 分, 共 24 分,把答案填在题中横线上.)}
(9) 曲面 z = x 2 ( 1 − sin y ) + y 2 ( 1 − sin x ) z=x^{2}(1-\sin y)+y^{2}(1-\sin x) z = x 2 ( 1 − sin y ) + y 2 ( 1 − sin x ) ( 1 , 0 , 1 ) (1,0,1) ( 1 , 0 , 1 )
(9) 曲面的切平面 : 设曲面 Σ \displaystyle \Sigma Σ F ( x , y , z ) = 0 F(x, y, z)=0 F ( x , y , z ) = 0 M ( x 0 , y 0 , z 0 ) M\left(x_0, y_0, z_0\right) M ( x 0 , y 0 , z 0 ) Σ \displaystyle \Sigma Σ F ( x , y , z ) F(x, y, z) F ( x , y , z ) 向量n = ( F x ′ ( x 0 , y 0 , z 0 ) , F y ′ ( x 0 , y 0 , z 0 ) , F z ′ ( x 0 , y 0 , z 0 ) ) \boldsymbol{n}=\left(F_x^{\prime}\left(x_0, y_0, z_0\right), F_y^{\prime}\left(x_0, y_0, z_0\right), F_z^{\prime}\left(x_0, y_0, z_0\right)\right) n = ( F x ′ ( x 0 , y 0 , z 0 ) , F y ′ ( x 0 , y 0 , z 0 ) , F z ′ ( x 0 , y 0 , z 0 ) ) Σ \displaystyle \Sigma Σ M M M 该切平面的方程为F x ′ ( x 0 , y 0 , z 0 ) ( X − x 0 ) + F y ′ ( x 0 , y 0 , z 0 ) ( Y − y 0 ) + F z ′ ( x 0 , y 0 , z 0 ) ( Z − z 0 ) F_x^{\prime}\left(x_0, y_0, z_0\right)\left(X-x_0\right)+F_y^{\prime}\left(x_0, y_0, z_0\right)\left(Y-y_0\right)+F_z^{\prime}\left(x_0, y_0, z_0\right)\left(Z-z_0\right) F x ′ ( x 0 , y 0 , z 0 ) ( X − x 0 ) + F y ′ ( x 0 , y 0 , z 0 ) ( Y − y 0 ) + F z ′ ( x 0 , y 0 , z 0 ) ( Z − z 0 ) 求曲面 z = x 2 ( 1 − sin y ) + y 2 ( 1 − sin x ) z=x^2(1-\sin y)+y^2(1-\sin x) z = x 2 ( 1 − sin y ) + y 2 ( 1 − sin x ) ( 1 , 0 , 1 ) (1,0,1) ( 1 , 0 , 1 ) F x ′ = 2 ( 1 − sin y ) ⋅ x − y 2 cos x \displaystyle \begin{aligned} & F_x^{\prime}=2(1-\sin y) \cdot x-y^2 \cos x \end{aligned} F x ′ = 2 ( 1 − sin y ) ⋅ x − y 2 cos x F y ′ = − x 2 cos y + 2 ( 1 − sin x ) y \displaystyle \begin{aligned}F_y^{\prime}=-x^2 \cos y+2(1-\sin x) y\end{aligned} F y ′ = − x 2 cos y + 2 ( 1 − sin x ) y F z ′ = − 1 \displaystyle \begin{aligned} F_z^{\prime}=-1 \end{aligned} F z ′ = − 1 n ⃗ = ( F x ′ , F y ′ , F z ′ ) ∣ ( 1 , 0 , 1 ) = ( 2 , − 1 , − 1 ) \displaystyle \begin{aligned} \vec{n}=\left.\left(F_x^{\prime}, F_y^{\prime}, F_z^{\prime}\right)\right|_{(1,0,1)}=(2,-1,-1) \end{aligned} n = ( F x ′ , F y ′ , F z ′ ) ( 1 , 0 , 1 ) = ( 2 , − 1 , − 1 ) 代入切平面方程为 2 ( x − 1 ) + ( − 1 ) ( y − 0 ) + ( − 1 ) ( z − 1 ) = 0 2(x-1)+(-1)(y-0)+(-1)(z-1)=0 2 ( x − 1 ) + ( − 1 ) ( y − 0 ) + ( − 1 ) ( z − 1 ) = 0 即 2 x − y − z − 1 = 0 2 x-y-z-1=0 2 x − y − z − 1 = 0 (10) 设 f ( x ) f(x) f ( x ) f ′ ( x ) = 2 ( x − 1 ) , x ∈ [ 0 , 2 ] f^{\prime}(x)=2(x-1), x \in[0,2] f ′ ( x ) = 2 ( x − 1 ) , x ∈ [ 0 , 2 ] f ( 7 ) = f(7)= f ( 7 ) =
(10) 问题: 求 f ( 7 ) f(7) f ( 7 ) f ( x ) f(x) f ( x ) f ′ ( x ) = 2 ( x − 1 ) f^{\prime}(x) = 2(x-1) f ′ ( x ) = 2 ( x − 1 ) x ∈ [ 0 , 2 ] x \in[0,2] x ∈ [ 0 , 2 ] 求导函数的原函数: 积分: f ( x ) = ∫ f ′ ( x ) d x = ∫ 2 ( x − 1 ) d x \displaystyle f(x) = \int f^{\prime}(x) \, \mathrm{d}x = \int 2(x-1) \, \mathrm{d}x f ( x ) = ∫ f ′ ( x ) d x = ∫ 2 ( x − 1 ) d x 结果: f ( x ) = x 2 − 2 x + C f(x) = x^2 - 2x + C f ( x ) = x 2 − 2 x + C 利用奇函数性质确定 C: 奇函数性质: f ( 0 ) = 0 f(0) = 0 f ( 0 ) = 0 确定的原函数: f ( x ) = x 2 − 2 x f(x) = x^2 - 2x f ( x ) = x 2 − 2 x 利用周期性求 f ( 7 ) f(7) f ( 7 ) 周期性: f ( 7 ) = f ( 7 m o d 4 ) = f ( 3 ) f(7) = f(7 \mod 4) = f(3) f ( 7 ) = f ( 7 mod 4 ) = f ( 3 ) 奇函数性质: f ( 3 ) = f ( − 1 ) f(3) = f(-1) f ( 3 ) = f ( − 1 ) 再次利用奇函数性质: f ( − 1 ) = − f ( 1 ) f(-1) = -f(1) f ( − 1 ) = − f ( 1 ) 计算 f ( 1 ) f(1) f ( 1 ) f ( 1 ) = 1 2 − 2 × 1 = − 1 f(1) = 1^2 - 2 \times 1 = -1 f ( 1 ) = 1 2 − 2 × 1 = − 1 结果: f ( 7 ) = − f ( 1 ) = 1 f(7) = -f(1) = 1 f ( 7 ) = − f ( 1 ) = 1 (11) 微分方程 x y ′ + y ( ln x − ln y ) = 0 x y^{\prime}+y(\ln x-\ln y)=0 x y ′ + y ( ln x − ln y ) = 0 y ( 1 ) = e 3 y(1)=\mathrm{e}^{3} y ( 1 ) = e 3 y = y= y =
(11) 答 应填 x e 2 x + 1 x \mathrm{e}^{2 x+1} x e 2 x + 1 y ′ = y x ( ln y − ln x ) = y x ⋅ ln ( y x ) = u \cdotp l n u y^{\prime}=\frac{y}{x}(\ln y-\ln x)=\frac{y}{x} \cdot \ln \left(\frac{y}{x}\right)=u\text{·}lnu y ′ = x y ( ln y − ln x ) = x y ⋅ ln ( x y ) = u \cdotp l n u 方程的标准形式为 d y d x = y x ln y x \frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{y}{x} \ln \frac{y}{x} d x d y = x y ln x y 设 u = y x u=\frac{y}{x} u = x y d y d x = u + x d u d x \frac{\mathrm{d} y}{\mathrm{~d} x}=u+x \frac{\mathrm{d} u}{\mathrm{~d} x} d x d y = u + x d x d u 原方程化为 u + x d u d x = u ln u u+x \frac{\mathrm{d} u}{\mathrm{~d} x}=u \ln u u + x d x d u = u ln u → 分离变量 ∫ d u f ( u ) − u = ∫ d x x d u u ( ln u − 1 ) = d x x \displaystyle \begin{aligned}\xrightarrow[\text{分离变量}]{\int \frac{d u}{f(u)-u}=\int \frac{d x}{x}}\frac{d u}{u(\ln u-1)}=\frac{d x}{x}\end{aligned} ∫ f ( u ) − u d u = ∫ x d x 分离变量 u ( ln u − 1 ) d u = x d x 两端积分,d ( ln u − 1 ) ln u − 1 = d x x \displaystyle \begin{aligned} \frac{\mathrm{d}(\ln u-1)}{\ln u-1}=\frac{\mathrm{d} x}{x} \end{aligned} ln u − 1 d ( ln u − 1 ) = x d x ln ∣ ln u − 1 ∣ = ln x + C 1 , \displaystyle \begin{aligned} \ln |\ln u-1|=\ln x+C_1, \end{aligned} ln ∣ ln u − 1∣ = ln x + C 1 , ln u − 1 = C x \displaystyle \begin{aligned} \ln u-1=C x \end{aligned} ln u − 1 = C x 代回原变量 u = y x \displaystyle \begin{aligned}u=\frac{y}{x}\end{aligned} u = x y ln y x − 1 = C x . \ln \frac{y}{x}-1=C x . ln x y − 1 = C x . 将 y ( 1 ) = e 3 \displaystyle \begin{aligned} y(1) = e^3 \end{aligned} y ( 1 ) = e 3 3 − 1 = C \displaystyle \begin{aligned} & 3-1=C \end{aligned} 3 − 1 = C C = 2 \displaystyle \begin{aligned} C = 2 \end{aligned} C = 2 ln y x = 2 x + 1 \displaystyle \begin{aligned} \ln \frac{y}{x}=2 x+1 \end{aligned} ln x y = 2 x + 1 于是 ln y x = 2 x + 1 \displaystyle \begin{aligned} \ln \frac{y}{x} = 2x + 1 \end{aligned} ln x y = 2 x + 1 y = x e 2 x + 1 . \displaystyle \begin{aligned} y = xe^{2x+1}. \end{aligned} y = x e 2 x + 1 . 齐次方程的解法:d y d x = f ( y x ) = f ( u ) \frac{d y}{d x}=f\left(\frac{y}{x}\right)=f(u) d x d y = f ( x y ) = f ( u ) 令 y x = u \frac{y}{x}=u x y = u y = u x y=u x y = ux f ( u ) = d y d x = u + x d u d x f(u)=\frac{d y}{d x}=u+x \frac{d u}{d x} f ( u ) = d x d y = u + x d x d u 代入可得u + x d u d x = f ( u ) u+x \frac{d u}{d x}=f(u) u + x d x d u = f ( u ) 可分离变量并积分, 得∫ d u f ( u ) − u = ∫ d x x , f ( u ) − u ≠ 0 \displaystyle \int \frac{d u}{f(u)-u}=\int \frac{d x}{x}, f(u)-u \neq 0 ∫ f ( u ) − u d u = ∫ x d x , f ( u ) − u = 0 (12) 设 L L L x 2 + y 2 = 1 x^{2}+y^{2}=1 x 2 + y 2 = 1 y + z = 0 y+z=0 y + z = 0 z z z z z z ∮ L z d x + y d z = \oint_{L} z \mathrm{~d} x+y \mathrm{~d} z= ∮ L z d x + y d z =
(12) 答 应填 π \pi π 斯托克斯如何判断法向量 右手螺旋准则,如果右手大拇指是朝上的z就为+1,如果是朝下的z就为-1 设平面 Σ : y + z = 0 \displaystyle \Sigma: y+z=0 Σ : y + z = 0 n = ( 0 , 1 , 1 ) n=(0,1,1) n = ( 0 , 1 , 1 ) n ∘ = ( 0 , 1 2 , 1 2 ) \boldsymbol{n}^{\circ}=\left(0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right) n ∘ = ( 0 , 2 1 , 2 1 ) 可知∮ L z d x + y d z = ∬ Σ ∣ 0 1 2 1 2 ∂ ∂ x ∂ ∂ y ∂ ∂ z z 0 y ∣ d S = 按第一行展开 1 2 ∬ Σ d S \displaystyle \begin{aligned} \oint_L z \mathrm{~d} x+y \mathrm{~d} z & =\iint_{\Sigma}\left|\begin{array}{ccc}0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\z & 0 & y\end{array}\right| \mathrm{d} S\xlongequal[]{\text{按第一行展开}}\frac{1}{\sqrt{2}} \iint_{\Sigma} \mathrm{d} S \end{aligned} ∮ L z d x + y d z = ∬ Σ 0 ∂ x ∂ z 2 1 ∂ y ∂ 0 2 1 ∂ z ∂ y d S 按第一行展开 2 1 ∬ Σ d S = 转换投影法 ∬ D 2 2 z x 2 + z y 2 + 1 d x \displaystyle \begin{aligned}\xlongequal[]{\text{转换投影法}}\iint_D \frac{\sqrt{2}}{2} \sqrt{z_x^2+z_y^2+1} d x\end{aligned} 转换投影法 ∬ D 2 2 z x 2 + z y 2 + 1 d x = z = − y 求导 1 2 ∬ D x y 0 2 + ( − 1 ) 2 + 1 d x d y \displaystyle \begin{aligned}\xlongequal[]{z=-y\text{求导}}\frac{1}{\sqrt{2}} \iint_{D_{x y}} \sqrt{0^2+(-1)^2+1} \mathrm{~d} x \mathrm{d} y\end{aligned} z = − y 求导 2 1 ∬ D x y 0 2 + ( − 1 ) 2 + 1 d x d y 其中 D x y = { ( x , y ) ∣ x 2 + y 2 ⩽ 1 } D_{x y}=\left\{(x, y) \mid x^2+y^2 \leqslant 1\right\} D x y = { ( x , y ) ∣ x 2 + y 2 ⩽ 1 } Σ \displaystyle \Sigma Σ x O y x O y x O y = ∬ D 1 d x d y = π \displaystyle \begin{aligned}=\iint_D 1 d x d y=\pi\end{aligned} = ∬ D 1 d x d y = π 斯托克斯公式的定义: ∮ L P d x + Q d y + R d z = ∬ Σ ∣ cos α cos β cos γ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ d S \displaystyle \begin{aligned}\oint_L P \mathrm{~d} x+Q \mathrm{~d} y+R \mathrm{~d} z=\iint_{\Sigma}\left|\begin{array}{ccc}\cos \alpha & \cos \beta & \cos \gamma \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R\end{array}\right| \mathrm{d} S\end{aligned} ∮ L P d x + Q d y + R d z = ∬ Σ cos α ∂ x ∂ P cos β ∂ y ∂ Q cos γ ∂ z ∂ R d S (13) 设二次型 f ( x 1 , x 2 , x 3 ) = x 1 2 − x 2 2 + 2 a x 1 x 3 + 4 x 2 x 3 f\left(x_{1}, x_{2}, x_{3}\right)=x_{1}^{2}-x_{2}^{2}+2 a x_{1} x_{3}+4 x_{2} x_{3} f ( x 1 , x 2 , x 3 ) = x 1 2 − x 2 2 + 2 a x 1 x 3 + 4 x 2 x 3 a a a
(13) 答 应填 [ − 2 , 2 ] [-2,2] [ − 2 , 2 ] f ( x 1 , x 2 , x 3 ) = x 1 2 − x 2 2 + 2 a x 1 x 3 + 4 x 2 x 3 = x 1 2 + 2 a x 1 x 3 + a 2 x 3 2 − x 2 2 + 4 x 2 x 3 − 4 x 3 2 + 4 x 3 2 − a 2 x 3 2 = ( x 1 + a x 3 ) 2 − ( x 2 − 2 x 3 ) 2 + ( 4 − a 2 ) x 3 2 \displaystyle \begin{aligned} f\left(x_1, x_2, x_3\right)&=x_1^2-x_2^2+2 a x_1 x_3+4 x_2 x_3 \\& =x_1^2+2 a x_1 x_3+a^2 x_3^2-x_2^2+4 x_2 x_3-4 x_3^2+4 x_3^2-a^2 x_3^2 \\ &=\left(x_1+a x_3\right)^2-\left(x_2-2 x_3\right)^2+\left(4-a^2\right) x_3^2 \end{aligned} f ( x 1 , x 2 , x 3 ) = x 1 2 − x 2 2 + 2 a x 1 x 3 + 4 x 2 x 3 = x 1 2 + 2 a x 1 x 3 + a 2 x 3 2 − x 2 2 + 4 x 2 x 3 − 4 x 3 2 + 4 x 3 2 − a 2 x 3 2 = ( x 1 + a x 3 ) 2 − ( x 2 − 2 x 3 ) 2 + ( 4 − a 2 ) x 3 2
因为 f f f 4 − a 2 ⩾ 0 4-a^2 \geqslant 0 4 − a 2 ⩾ 0 − 2 ⩽ a ⩽ 2 -2 \leqslant a \leqslant 2 − 2 ⩽ a ⩽ 2
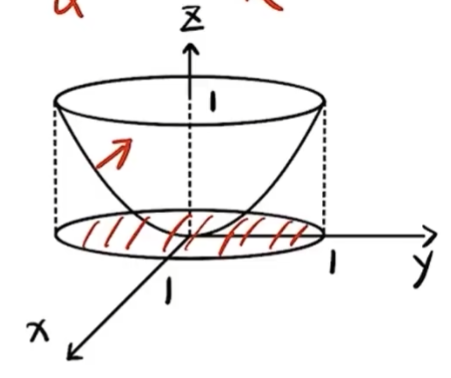
(14) 设总体 X X X f ( x ; θ ) = { 2 x 3 θ 2 , θ < x < 2 θ , 0 , 其他, \displaystyle f(x ; \theta)=\left\{\begin{array}{ll}\frac{2 x}{3 \theta^{2}}, & \theta<x<2 \theta, \\ 0, & \text { 其他, }\end{array}\right. f ( x ; θ ) = { 3 θ 2 2 x , 0 , θ < x < 2 θ , 其他 , θ \theta θ X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n X X X c ∑ i = 1 n X i 2 \displaystyle c \sum_{i=1}^{n} X_{i}^{2} c i = 1 ∑ n X i 2 θ 2 \theta^{2} θ 2 c = c= c =
(14) 答 应填 2 5 n \frac{2}{5 n} 5 n 2 E ( X 2 ) = ∫ θ 2 θ x 2 2 x 3 θ 2 d x = 5 2 θ 2 \displaystyle E\left(X^2\right)=\int_\theta^{2 \theta} x^2 \frac{2 x}{3 \theta^2} \mathrm{~d} x=\frac{5}{2} \theta^2 E ( X 2 ) = ∫ θ 2 θ x 2 3 θ 2 2 x d x = 2 5 θ 2 E ( c ∑ i = 1 n X i 2 ) = c n 5 2 θ 2 \displaystyle E\left(c \sum_{i=1}^n X_i^2\right)=c n \frac{5}{2} \theta^2 E ( c i = 1 ∑ n X i 2 ) = c n 2 5 θ 2 c ∑ i = 1 n X i 2 \displaystyle c \sum_{i=1}^n X_i^2 c i = 1 ∑ n X i 2 θ 2 \theta^2 θ 2 c n 5 2 = 1 c n \frac{5}{2}=1 c n 2 5 = 1 c = 2 5 n c=\frac{2}{5 n} c = 5 n 2 (15) (本题满分 10 分)求极限 lim x → + ∞ ∫ 1 x [ t 2 ( e 1 t − 1 ) − t ] d t x 2 ln ( 1 + 1 x ) \displaystyle \lim _{x \rightarrow+\infty} \frac{\int_{1}^{x}\left[t^{2}\left(\mathrm{e}^{\frac{1}{t}}-1\right)-t\right] \mathrm{d} t}{x^{2} \ln \left(1+\frac{1}{x}\right)} x → + ∞ lim x 2 ln ( 1 + x 1 ) ∫ 1 x [ t 2 ( e t 1 − 1 ) − t ] d t
(15) lim x → + ∞ ∫ 1 x [ t 2 ( e 1 t − 1 ) − t ] d t x 2 ln ( 1 + 1 x ) = 第一件事 化简分母 lim x → + ∞ ∫ 1 x [ t 2 ( e 1 t − 1 ) − t ] d t x \displaystyle \begin{aligned} \lim_{x \to +\infty} \frac{\int_{1}^{x} \left[ t^2 \left( e^{\frac{1}{t}} - 1 \right) - t \right] dt}{x^2 \ln \left( 1 + \frac{1}{x} \right)} \xlongequal[\text{第一件事}]{\text{化简分母}} \lim_{x \to +\infty} \frac{\int_{1}^{x} \left[ t^2 \left( e^{\frac{1}{t}} - 1 \right) - t \right] dt}{x} \end{aligned} x → + ∞ lim x 2 ln ( 1 + x 1 ) ∫ 1 x [ t 2 ( e t 1 − 1 ) − t ] d t 化简分母 第一件事 x → + ∞ lim x ∫ 1 x [ t 2 ( e t 1 − 1 ) − t ] d t 只要分母趋于 ∞ \displaystyle \begin{aligned} \infty \end{aligned} ∞ ∞ \displaystyle \begin{aligned} \infty \end{aligned} ∞ = 洛必达 lim x → + ∞ [ x 2 ( e 1 x − 1 ) − x ] \displaystyle \begin{aligned} \xlongequal[]{\text{洛必达}} \lim_{x \to +\infty} \left[ x^2 \left( e^{\frac{1}{x}} - 1 \right) - x \right] \end{aligned} 洛必达 x → + ∞ lim [ x 2 ( e x 1 − 1 ) − x ] ( 令 1 x = t ) = 倒代换 lim t → 0 + ( e ′ − 1 t 2 − 1 t ) \displaystyle \begin{aligned} \left( \text{令} \frac{1}{x} = t \right) \xlongequal[]{\text{倒代换}} \lim_{t \to 0^{+}} \left( \frac{e' - 1}{t^2} - \frac{1}{t} \right) \end{aligned} ( 令 x 1 = t ) 倒代换 t → 0 + lim ( t 2 e ′ − 1 − t 1 ) = 通分 lim t → 0 + e t − 1 − t t 2 = 泰勒 ( lim t → 0 + 1 2 t 2 ) = 1 2 . \displaystyle \begin{aligned}\xlongequal[]{\text{通分}}\lim_{t \to 0^{+}} \frac{e^t - 1 - t}{t^2} \xlongequal[]{\text{泰勒}} \left( \lim_{t \to 0^{+}} \frac{1}{2} t^2 \right) = \frac{1}{2}.\end{aligned} 通分 t → 0 + lim t 2 e t − 1 − t 泰勒 ( t → 0 + lim 2 1 t 2 ) = 2 1 . (16) (本题满分 10 分)设函数 y = f ( x ) y=f(x) y = f ( x ) y 3 + x y 2 + x 2 y + 6 = 0 y^{3}+x y^{2}+x^{2} y+6=0 y 3 + x y 2 + x 2 y + 6 = 0 f ( x ) f(x) f ( x )
(16) 对方程求一阶导 对方程 y 3 + x y 2 + x 2 y + 6 = 0 y^3 + x y^2 + x^2 y + 6 = 0 y 3 + x y 2 + x 2 y + 6 = 0 x x x 得到 3 y 2 y ′ + y 2 + 2 x y y ′ + 2 x y + x 2 y ′ = 0 3 y^2 y' + y^2 + 2 x y y' + 2 x y + x^2 y' = 0 3 y 2 y ′ + y 2 + 2 x y y ′ + 2 x y + x 2 y ′ = 0 求 f ( 1 ) f(1) f ( 1 ) 令 y ′ = 0 y' = 0 y ′ = 0 y = − 2 x y = -2x y = − 2 x y = 0 y = 0 y = 0 y = 0 y = 0 y = 0 使用 y = − 2 x y = -2x y = − 2 x x = 1 x = 1 x = 1 f ( 1 ) = − 2 f(1) = -2 f ( 1 ) = − 2 对导数方程再次求导二阶导 对导数方程 3 y 2 y ′ + y 2 + 2 x y y ′ + 2 x y + x 2 y ′ = 0 3 y^2 y' + y^2 + 2 x y y' + 2 x y + x^2 y' = 0 3 y 2 y ′ + y 2 + 2 x y y ′ + 2 x y + x 2 y ′ = 0 x x x 得到 ( 3 y 2 + 2 x y + x 2 ) y ′ ′ + 2 ( 3 y + x ) ( y ′ ) 2 + 4 ( y + x ) y ′ + 2 y = 0 \left(3 y^2 + 2 x y + x^2\right) y'' + 2(3 y + x)(y')^2 + 4(y + x) y' + 2 y = 0 ( 3 y 2 + 2 x y + x 2 ) y ′′ + 2 ( 3 y + x ) ( y ′ ) 2 + 4 ( y + x ) y ′ + 2 y = 0 求二阶导数 f ′ ′ ( 1 ) f''(1) f ′′ ( 1 ) 将 x = 1 x = 1 x = 1 y = f ( 1 ) = − 2 y =f(1) =-2 y = f ( 1 ) = − 2 解得 f ′ ′ ( 1 ) = 4 9 > 0 f''(1) = \frac{4}{9} > 0 f ′′ ( 1 ) = 9 4 > 0 x = 1 x=1 x = 1 f ( x ) f(x) f ( x ) f ( 1 ) = − 2 f(1)=-2 f ( 1 ) = − 2 (17) (本题满分 10 分)设函数 f ( u ) f(u) f ( u ) z = f ( e x cos y ) z=f\left(\mathrm{e}^{x} \cos y\right) z = f ( e x cos y ) ∂ 2 z ∂ x 2 + ∂ 2 z ∂ y 2 = ( 4 z + e x cos y ) e 2 x \frac{\partial^{2} z}{\partial x^{2}}+\frac{\partial^{2} z}{\partial y^{2}}=\left(4 z+\mathrm{e}^{x} \cos y\right) \mathrm{e}^{2 x} ∂ x 2 ∂ 2 z + ∂ y 2 ∂ 2 z = ( 4 z + e x cos y ) e 2 x f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 f ′ ( 0 ) = 0 f^{\prime}(0)=0 f ′ ( 0 ) = 0 f ( u ) f(u) f ( u )
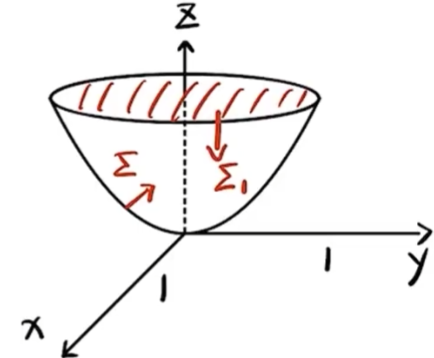
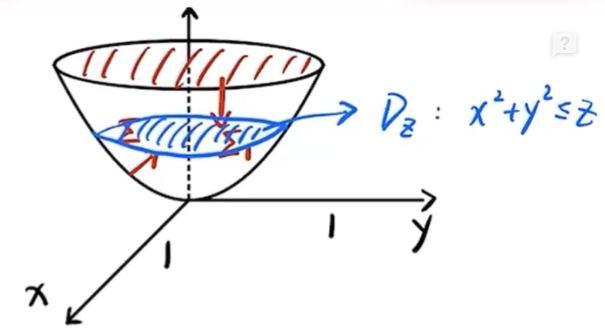
(17) 解题步骤 计算 ∂ 2 z ∂ x 2 , ∂ 2 z ∂ y 2 \frac{\partial^2 z}{\partial x^2}, \frac{\partial^2 z}{\partial y^2} ∂ x 2 ∂ 2 z , ∂ y 2 ∂ 2 z 将 ∂ 2 z ∂ x 2 , ∂ 2 z ∂ y 2 \frac{\partial^2 z}{\partial x^2}, \frac{\partial^2 z}{\partial y^2} ∂ x 2 ∂ 2 z , ∂ y 2 ∂ 2 z 解微分方程求得 f ( u ) f(u) f ( u ) 计算 ∂ 2 z ∂ x 2 , ∂ 2 z ∂ y 2 \frac{\partial^2 z}{\partial x^2}, \frac{\partial^2 z}{\partial y^2} ∂ x 2 ∂ 2 z , ∂ y 2 ∂ 2 z ∂ z ∂ x = f ′ ( e x cos y ) ⋅ e x cos y \displaystyle \begin{aligned} \frac{\partial z}{\partial x} & =f^{\prime}\left(e^x \cos y\right) \cdot e^x \cos y\end{aligned} ∂ x ∂ z = f ′ ( e x cos y ) ⋅ e x cos y ∂ z ∂ x 2 = e x cos y ⋅ f ′ ( e x cos y ) + e x cos y [ f ′ ′ ( e x cos y ) ⋅ e x cos y ] \displaystyle \begin{aligned}\frac{\partial z}{\partial x^2} & =e^x \cos y \cdot f^{\prime}\left(e^x \cos y\right)+e^x \cos y\left[f^{\prime \prime}\left(e^x \cos y\right) \cdot e^x \cos y\right]\end{aligned} ∂ x 2 ∂ z = e x cos y ⋅ f ′ ( e x cos y ) + e x cos y [ f ′′ ( e x cos y ) ⋅ e x cos y ] = e x cos y ⋅ f ′ ( e x cos y ) + e 2 x cos y f ′ ′ ( e x cos y ) \displaystyle \begin{aligned} =e^x \cos y \cdot f^{\prime}\left(e^x \cos y\right)+e^{2 x} \cos y f^{\prime \prime}\left(e^x \cos y\right)\end{aligned} = e x cos y ⋅ f ′ ( e x cos y ) + e 2 x cos y f ′′ ( e x cos y ) ∂ z ∂ y = f ′ ( e x cos y ) ⋅ ( − e x sin y ) \displaystyle \begin{aligned}\frac{\partial z}{\partial y} & =f^{\prime}\left(e^x \cos y\right) \cdot\left(-e^x \sin y\right)\end{aligned} ∂ y ∂ z = f ′ ( e x cos y ) ⋅ ( − e x sin y ) ∂ z 2 ∂ y 2 = − e x cos y ⋅ f ′ ( e x cos y ) + ( − e x sin y ) [ f ′ ′ ( e x cos y ) ⋅ ( − e x sin y ) ] \displaystyle \begin{aligned} \frac{\partial z^2}{\partial y^2} & =-e^x \cos y \cdot f^{\prime}\left(e^x \cos y\right)+\left(-e^x \sin y\right)\left[f^{\prime \prime}\left(e^x \cos y\right) \cdot\left(-e^x \sin y\right)\right] \end{aligned} ∂ y 2 ∂ z 2 = − e x cos y ⋅ f ′ ( e x cos y ) + ( − e x sin y ) [ f ′′ ( e x cos y ) ⋅ ( − e x sin y ) ] = − e x cos y ⋅ f ′ ( e x cos y ) + e 2 x sin y f ′ ′ ( e x cos y ) \displaystyle \begin{aligned} =-e^x \cos y \cdot f^{\prime}\left(e^x \cos y\right)+e^{2 x} \sin y f^{\prime \prime}\left(e^x \cos y\right) \end{aligned} = − e x cos y ⋅ f ′ ( e x cos y ) + e 2 x sin y f ′′ ( e x cos y ) 将 ∂ 2 z ∂ x 2 , ∂ 2 z ∂ y 2 \frac{\partial^2 z}{\partial x^2}, \frac{\partial^2 z}{\partial y^2} ∂ x 2 ∂ 2 z , ∂ y 2 ∂ 2 z ∂ 2 z ∂ x 2 + ∂ 2 z ∂ y 2 = e 2 x f ′ ′ ( e x cos y ) ( cos 2 y + sin 2 y ) → cos 2 y + sin 2 y = 1 e 2 x f ′ ′ ( e x cos y ) \displaystyle \begin{aligned} \frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = e^{2x} f''(e^x \cos y)(\cos^2 y + \sin^2 y) \xrightarrow[]{\cos^2 y + \sin^2 y=1}e^{2x} f''(e^x \cos y)\end{aligned} ∂ x 2 ∂ 2 z + ∂ y 2 ∂ 2 z = e 2 x f ′′ ( e x cos y ) ( cos 2 y + sin 2 y ) c o s 2 y + s i n 2 y = 1 e 2 x f ′′ ( e x cos y ) 题目给定:∂ 2 z ∂ x 2 + ∂ 2 z ∂ y 2 = ( 4 z + e x cos y ) e 2 x \displaystyle \begin{aligned}\frac{\partial^{2} z}{\partial x^{2}}+\frac{\partial^{2} z}{\partial y^{2}}=\left(4 z+\mathrm{e}^{x} \cos y\right) \mathrm{e}^{2 x}\end{aligned} ∂ x 2 ∂ 2 z + ∂ y 2 ∂ 2 z = ( 4 z + e x cos y ) e 2 x 则e 2 x f ′ ′ ( e x cos y ) = ( 4 z + e x cos y ) e 2 x \displaystyle \begin{aligned} e^{2x} f''(e^x \cos y) = (4z + e^x \cos y) e^{2x} \end{aligned} e 2 x f ′′ ( e x cos y ) = ( 4 z + e x cos y ) e 2 x → 去掉 e 2 x f ′ ′ ( e x cos y ) = 4 f ( e x cos y ) + e x cos y \displaystyle \begin{aligned} \xrightarrow[]{\text{去掉}e^{2x}}f''(e^x \cos y) = 4f(e^x \cos y) + e^x \cos y \end{aligned} 去掉 e 2 x f ′′ ( e x cos y ) = 4 f ( e x cos y ) + e x cos y 令 u = e x cos y \displaystyle \begin{aligned} u = e^x \cos y \end{aligned} u = e x cos y f ′ ′ ( u ) = 4 f ( u ) + u \displaystyle \begin{aligned} f''(u) = 4f(u) + u \end{aligned} f ′′ ( u ) = 4 f ( u ) + u 解微分方程求得 f ( u ) f(u) f ( u ) 二阶非齐次微分方程f ′ ′ ( u ) − 4 f ( u ) = u \displaystyle \begin{aligned} & f^{\prime \prime}(u)-4 f(u)=u \end{aligned} f ′′ ( u ) − 4 f ( u ) = u 特征方程:r 2 − 4 = 0 ⇒ r = ± 2 \displaystyle \begin{aligned} r^2-4=0 \Rightarrow r= \pm 2 \end{aligned} r 2 − 4 = 0 ⇒ r = ± 2 y = C 1 e 2 u + C 2 e − 2 u \displaystyle \begin{aligned} y=C_1 e^{2 u}+C_2 e^{-2 u} \end{aligned} y = C 1 e 2 u + C 2 e − 2 u 求特解 由于 0 不是特征方程的根, 故设特解为 y ∗ = x 0 \cdotp ( C 3 u + C 4 ) = C 3 u + C 4 y^*=x^0\text{·}(C_3 u+C_4)=C_3 u+C_4 y ∗ = x 0 \cdotp ( C 3 u + C 4 ) = C 3 u + C 4 ( y ∗ ) ′ ′ = 0 \left(y^*\right)^{\prime \prime}=0 ( y ∗ ) ′′ = 0 将y 和 y ′ ′ y\text{和}y'' y 和 y ′′ f ′ ′ ( u ) − 4 f ( u ) = u f^{\prime \prime}(u)-4 f(u)=u f ′′ ( u ) − 4 f ( u ) = u 得0 − 4 C 3 u − 4 C 4 = u 0-4 C_3 u-4 C_4=u 0 − 4 C 3 u − 4 C 4 = u 于是 C 3 = − 1 4 , C 4 = 0 C_3=-\frac{1}{4}, C_4=0 C 3 = − 4 1 , C 4 = 0 从而确定C 3 C_3 C 3 C 4 C_4 C 4 f ( u ) = C 1 e 2 u + C 2 e − 2 u − 1 4 u . f(u)=C_1 \mathrm{e}^{2 u}+C_2 \mathrm{e}^{-2 u}-\frac{1}{4} u . f ( u ) = C 1 e 2 u + C 2 e − 2 u − 4 1 u . 代入f ( u ) = C 1 e 2 u + C 2 e − 2 u − 1 4 u . f(u)=C_1 \mathrm{e}^{2 u}+C_2 \mathrm{e}^{-2 u}-\frac{1}{4} u . f ( u ) = C 1 e 2 u + C 2 e − 2 u − 4 1 u . C 1 , C 2 C_1, C_2 C 1 , C 2 由 f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 C 1 + C 2 = 0 C_1+C_2=0 C 1 + C 2 = 0 由 f ′ ( 0 ) = 0 f^{\prime}(0)=0 f ′ ( 0 ) = 0 2 C 1 − 2 C 2 − 1 4 = 0 2 C_1-2 C_2-\frac{1}{4}=0 2 C 1 − 2 C 2 − 4 1 = 0 从而解得 C 1 = 1 16 , C 2 = − 1 16 C_1=\frac{1}{16}, C_2=-\frac{1}{16} C 1 = 16 1 , C 2 = − 16 1 因此, 非齐次的通解为齐次通解+特解为f ( u ) = 1 16 e 2 u − 1 16 e − 2 u − 1 4 u \displaystyle \begin{aligned}f(u)=\frac{1}{16} \mathrm{e}^{2 u}-\frac{1}{16} \mathrm{e}^{-2 u}-\frac{1}{4} u\end{aligned} f ( u ) = 16 1 e 2 u − 16 1 e − 2 u − 4 1 u (2006 年数一、二试题) 设函数 f ( u ) f(u) f ( u ) ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ ) z = f ( x 2 + y 2 ) z=f\left(\sqrt{x^2+y^2}\right) z = f ( x 2 + y 2 ) ∂ 2 z ∂ x 2 + ∂ 2 z ∂ y 2 = 0. \frac{\partial^2 z}{\partial x^2}+\frac{\partial^2 z}{\partial y^2}=0 . ∂ x 2 ∂ 2 z + ∂ y 2 ∂ 2 z = 0. f ′ ′ ( u ) + f ′ ( u ) u = 0 f^{\prime \prime}(u)+\frac{f^{\prime}(u)}{u}=0 f ′′ ( u ) + u f ′ ( u ) = 0 f ( 1 ) = 0 , f ′ ( 1 ) = 1 f(1)=0, f^{\prime}(1)=1 f ( 1 ) = 0 , f ′ ( 1 ) = 1 f ( u ) f(u) f ( u ) (18) (本题满分 10 分)设 Σ \displaystyle \Sigma Σ z = x 2 + y 2 ( z ⩽ 1 ) z=x^{2}+y^{2}(z \leqslant 1) z = x 2 + y 2 ( z ⩽ 1 ) I = ∬ Σ ( x − 1 ) 3 d y d z + ( y − 1 ) 3 d z d x + ( z − 1 ) d x d y . \displaystyle I=\iint_{\Sigma}(x-1)^{3} \mathrm{~d} y \mathrm{~d} z+(y-1)^{3} \mathrm{~d} z \mathrm{~d} x+(z-1) \mathrm{d} x \mathrm{~d} y . I = ∬ Σ ( x − 1 ) 3 d y d z + ( y − 1 ) 3 d z d x + ( z − 1 ) d x d y .
(18) 转换投影法 D : { ( x , y ) ∣ x 2 + y 2 ≤ 1 } \displaystyle \begin{aligned} D: \left\{(x, y) \mid x^{2} + y^{2} \leq 1\right\}\end{aligned} D : { ( x , y ) ∣ x 2 + y 2 ≤ 1 } I = ∬ D ( − P z x − Q z y + R ) d x d y \displaystyle \begin{aligned} I = \iint_{D} (-Pzx - Qzy + R) \, dx \, dy \end{aligned} I = ∬ D ( − P z x − Q zy + R ) d x d y = ∬ D [ − ( x − 1 ) 3 ⋅ 2 x − ( y − 1 ) 3 ⋅ 2 y + ( z − 1 ) ] d x d y \displaystyle \begin{aligned} = \iint_{D} \left[-(x-1)^{3} \cdot 2x - (y-1)^{3} \cdot 2y + (z-1)\right] \, dx \, dy \end{aligned} = ∬ D [ − ( x − 1 ) 3 ⋅ 2 x − ( y − 1 ) 3 ⋅ 2 y + ( z − 1 ) ] d x d y = ∬ D [ ( x 3 − 3 x 2 + 3 x − x 3 ) ⋅ 2 x + ( x 3 − 3 y 2 + 3 y 2 − y 3 ) ⋅ 2 y + x 2 + y 2 ⏟ z − 1 ] d x d y \displaystyle \begin{aligned} = \iint_{D} \left[(x^3 - 3x^2 + 3x - x^3) \cdot 2x + (x^3 - 3y^2 + 3y^2 - y^3) \cdot 2y + \underbrace{x^2 + y^2}_{z} - 1\right] \, dx \, dy \end{aligned} = ∬ D [ ( x 3 − 3 x 2 + 3 x − x 3 ) ⋅ 2 x + ( x 3 − 3 y 2 + 3 y 2 − y 3 ) ⋅ 2 y + z x 2 + y 2 − 1 ] d x d y = 偶倍奇 0 积分区域关于 x , y 都对称 ∬ D [ − 6 x 2 − 2 x 4 − 6 y 2 − 2 y 4 + x 2 + y 2 − 1 ] d x d y \displaystyle \begin{aligned} \xlongequal[\text{偶倍奇}0]{\text{积分区域关于}x,y\text{都对称}} \iint_{D} \left[-6x^2 - 2x^4 - 6y^2 - 2y^4 + x^2 + y^2 - 1\right] \, dx \, dy \end{aligned} 积分区域关于 x , y 都对称 偶倍奇 0 ∬ D [ − 6 x 2 − 2 x 4 − 6 y 2 − 2 y 4 + x 2 + y 2 − 1 ] d x d y = ∬ D [ − 5 ( x 2 + y 2 ) − 2 ( x 4 + y 4 ) − 1 ] d x d y \displaystyle \begin{aligned} & =\iint_D\left[-5\left(x^2+y^2\right)-2\left(x^4+y^4\right)-1\right] d x d y \end{aligned} = ∬ D [ − 5 ( x 2 + y 2 ) − 2 ( x 4 + y 4 ) − 1 ] d x d y = 翻 4 倍 只算第一象限 − 20 ∬ D 1 ( x 2 + y 2 ) d x d y − 8 ∬ D 1 ( x 4 + y 4 ) d x d y − π \displaystyle \begin{aligned}\xlongequal[\text{翻}4\text{倍}]{\text{只算第一象限}}-20 \iint_{D_1}\left(x^2+y^2\right) d x d y-8 \iint_{D_1}\left(x^4+y^4\right) d x d y-\pi \end{aligned} 只算第一象限 翻 4 倍 − 20 ∬ D 1 ( x 2 + y 2 ) d x d y − 8 ∬ D 1 ( x 4 + y 4 ) d x d y − π ∬ D 1 ( x 2 + y 2 ) d x d y = ∫ 0 π 2 d θ ∫ 0 1 r 3 d r = π 8 \displaystyle \begin{aligned} \iint_{D_1} (x^2 + y^2) \, dx \, dy = \int_{0}^{\frac{\pi}{2}} d\theta \int_{0}^{1} r^3 \, dr = \frac{\pi}{8} \end{aligned} ∬ D 1 ( x 2 + y 2 ) d x d y = ∫ 0 2 π d θ ∫ 0 1 r 3 d r = 8 π ∬ D 1 ( x 4 + y 4 ) d x d y = 轮换对称性 2 ∬ D 1 x 4 d x d y = 2 ∫ 0 π 2 d θ ∫ 0 1 r 4 cos 4 θ r d r \displaystyle \begin{aligned} \iint_{D_1} (x^4 + y^4) \, dx \, dy\xlongequal[]{\text{轮换对称性}}2 \iint_{D_1} x^4 \, dx \, dy = 2 \int_{0}^{\frac{\pi}{2}} d\theta \int_{0}^{1} r^4 \cos^4 \theta rdr \end{aligned} ∬ D 1 ( x 4 + y 4 ) d x d y 轮换对称性 2 ∬ D 1 x 4 d x d y = 2 ∫ 0 2 π d θ ∫ 0 1 r 4 cos 4 θ r d r = 2 ∫ 0 π 2 cos 4 θ d θ ∫ 0 1 r 5 d r \displaystyle \begin{aligned} = 2 \int_{0}^{\frac{\pi}{2}} \cos^4 \theta \, d\theta \int_{0}^{1} r^5 \, dr \end{aligned} = 2 ∫ 0 2 π cos 4 θ d θ ∫ 0 1 r 5 d r = 2 ⋅ 3 4 ⋅ 1 2 ⋅ π 2 ⋅ 1 6 = π 16 \displaystyle \begin{aligned} = 2 \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2} \cdot \frac{1}{6} = \frac{\pi}{16} \end{aligned} = 2 ⋅ 4 3 ⋅ 2 1 ⋅ 2 π ⋅ 6 1 = 16 π I = − 20 ⋅ π 8 − 8 ⋅ π 16 − π = − 5 2 π − π 2 − π = − 4 π \displaystyle \begin{aligned}I=-20 \cdot \frac{\pi}{8}-8 \cdot \frac{\pi}{16}-\pi=-\frac{5}{2} \pi-\frac{\pi}{2}-\pi=-4 \pi\end{aligned} I = − 20 ⋅ 8 π − 8 ⋅ 16 π − π = − 2 5 π − 2 π − π = − 4 π 高斯 Σ 1 : { ( x , y , z ) ∣ x 2 + y 2 ≤ 1 , z = 1 } , 向下 , \displaystyle \begin{aligned} \Sigma_1: \left\{(x, y, z) \mid x^2 + y^2 \leq 1, \, z = 1\right\}, \, \text{向下}, \end{aligned} Σ 1 : { ( x , y , z ) ∣ x 2 + y 2 ≤ 1 , z = 1 } , 向下 , 负方向的高斯,结果外面要加负号 Ω 1 = Σ 1 和 Σ 所围区域 . \displaystyle \begin{aligned} \Omega_1 = \Sigma_1 \text{和} \Sigma \text{所围区域}. \end{aligned} Ω 1 = Σ 1 和 Σ 所围区域 . I = ∬ Σ = ∬ Σ + Σ 1 − ∬ Σ 1 = − 4 π \displaystyle \begin{aligned} I = \iint_{\Sigma} = \iint_{\Sigma + \Sigma_1} - \iint_{\Sigma_1} =-4 \pi\end{aligned} I = ∬ Σ = ∬ Σ + Σ 1 − ∬ Σ 1 = − 4 π ∮ Σ + Σ 1 = − ∭ Ω ( P x + Q y + R z ) d V \displaystyle \begin{aligned} \oint_{\Sigma + \Sigma_1} = -\iiint_{\Omega} (Px + Qy + Rz) \, dV \end{aligned} ∮ Σ + Σ 1 = − ∭ Ω ( P x + Q y + R z ) d V = − ∭ Ω [ 3 ( x − 1 ) 2 + 3 ( y − 1 ) 2 + 1 ] d V \displaystyle \begin{aligned} = -\iiint_{\Omega} \left[3(x-1)^2 + 3(y-1)^2 + 1\right] \, dV \end{aligned} = − ∭ Ω [ 3 ( x − 1 ) 2 + 3 ( y − 1 ) 2 + 1 ] d V = 去括号 − ∭ Ω [ 3 x 2 − 6 x + 3 + 3 y 2 − 6 y + 3 + 1 ] d V \displaystyle \begin{aligned}\xlongequal[]{\text{去括号}}-\iiint_{\Omega}\left[3 x^2-6 x+3+3 y^2-6 y+3+1\right] d V\end{aligned} 去括号 − ∭ Ω [ 3 x 2 − 6 x + 3 + 3 y 2 − 6 y + 3 + 1 ] d V = − ∭ Ω [ 3 ( x 2 + y 2 ) + 7 ] d V → 截面法算 柱线法算 \displaystyle \begin{aligned}=-\iiint_{\Omega}\left[3\left(x^2+y^2\right)+7\right] d V\xrightarrow[\text{截面法算}]{\text{柱线法算}}\end{aligned} = − ∭ Ω [ 3 ( x 2 + y 2 ) + 7 ] d V 柱线法算 截面法算 = − ∫ 0 1 d z ∬ D z [ 3 ( x 2 + y 2 ) + 7 ] d x d y \displaystyle \begin{aligned} & =-\int_0^1 d z \iint_{D_z}\left[3\left(x^2+y^2\right)+7\right] d x d y \end{aligned} = − ∫ 0 1 d z ∬ D z [ 3 ( x 2 + y 2 ) + 7 ] d x d y = − ∫ 0 1 d z ∫ 0 2 π d θ ∫ 0 z ( 3 r 2 + 7 ) r ⏟ ( 3 r 3 + 7 τ ) d r → 3 4 r 4 + 7 2 r 2 ∣ 0 z = 3 4 z 2 + 7 2 z \displaystyle \begin{aligned} =-\int_0^1 d z \int_0^{2 \pi} d \theta \int_0^{\sqrt{z}}\underbrace{\left(3 r^2+7\right) r}_{\left(3 r^3+7 \tau\right)}d r \xrightarrow[]{\frac{3}{4} r^4+\left.\frac{7}{2} r^2\right|_0 ^{\sqrt{z}}=\frac{3}{4} z^2+\frac{7}{2} z}\end{aligned} = − ∫ 0 1 d z ∫ 0 2 π d θ ∫ 0 z ( 3 r 3 + 7 τ ) ( 3 r 2 + 7 ) r d r 4 3 r 4 + 2 7 r 2 ∣ 0 z = 4 3 z 2 + 2 7 z = − ∫ 0 1 ( 3 2 π z 2 + 7 π z ) d z = − 4 π \displaystyle =-\int_0^1\left(\frac{3}{2} \pi z^2+7 \pi z\right) d z=-4 \pi = − ∫ 0 1 ( 2 3 π z 2 + 7 π z ) d z = − 4 π ∬ Σ 1 = 0 \displaystyle \iint_{\Sigma_1}=0 ∬ Σ 1 = 0 (19) (本题满分 10 分)设数列 { a n } , { b n } \left\{a_{n}\right\},\left\{b_{n}\right\} { a n } , { b n } 0 < a n < π 2 , 0 < b n < π 2 , cos a n − a n = cos b n 0<a_{n}<\frac{\pi}{2}, 0<b_{n}<\frac{\pi}{2}, \cos a_{n}-a_{n}=\cos b_{n} 0 < a n < 2 π , 0 < b n < 2 π , cos a n − a n = cos b n ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_{n} n = 1 ∑ ∞ b n lim n → ∞ a n = 0 \displaystyle \lim _{n \rightarrow \infty} a_{n}=0 n → ∞ lim a n = 0 ∑ n = 1 ∞ a n b n \displaystyle \sum_{n=1}^{\infty} \frac{a_{n}}{b_{n}} n = 1 ∑ ∞ b n a n
(19) 证 (I ) 因为 cos a n − cos b n = a n \cos a_n-\cos b_n=a_n cos a n − cos b n = a n 0 < a n < π 2 , 0 < b n < π 2 0<a_n<\frac{\pi}{2}, 0<b_n<\frac{\pi}{2} 0 < a n < 2 π , 0 < b n < 2 π 0 < a n < b n 0<a_n<b_n 0 < a n < b n ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_n n = 1 ∑ ∞ b n lim n → ∞ b n = 0 \displaystyle \lim _{n \rightarrow \infty} b_n=0 n → ∞ lim b n = 0 lim n → ∞ a n = 0 \displaystyle \lim _{n \rightarrow \infty} a_n=0 n → ∞ lim a n = 0 lim n → ∞ a n b n 2 = lim n → ∞ 1 − cos b n b n 2 ⋅ a n 1 − cos b n = 1 2 lim n → ∞ a n 1 − cos b n = 1 2 lim n → ∞ a n a n + 1 − cos a n = 1 2 \displaystyle \lim _{n \rightarrow \infty} \frac{a_n}{b_n^2}=\lim _{n \rightarrow \infty} \frac{1-\cos b_n}{b_n^2} \cdot \frac{a_n}{1-\cos b_n}=\frac{1}{2} \lim _{n \rightarrow \infty} \frac{a_n}{1-\cos b_n}=\frac{1}{2} \lim _{n \rightarrow \infty} \frac{a_n}{a_n+1-\cos a_n}=\frac{1}{2} n → ∞ lim b n 2 a n = n → ∞ lim b n 2 1 − cos b n ⋅ 1 − cos b n a n = 2 1 n → ∞ lim 1 − cos b n a n = 2 1 n → ∞ lim a n + 1 − cos a n a n = 2 1 ∑ n = 1 ∞ b n \displaystyle \sum_{n=1}^{\infty} b_n n = 1 ∑ ∞ b n ∑ n = 1 ∞ a n b n \displaystyle \sum_{n=1}^{\infty} \frac{a_n}{b_n} n = 1 ∑ ∞ b n a n (20) (本题满分 11 分)设 A = ( 1 − 2 3 − 4 0 1 − 1 1 1 2 0 − 3 ) , E \displaystyle \boldsymbol{A}=\left(\begin{array}{cccc}1 & -2 & 3 & -4 \\ 0 & 1 & -1 & 1 \\ 1 & 2 & 0 & -3\end{array}\right), \boldsymbol{E} A = 1 0 1 − 2 1 2 3 − 1 0 − 4 1 − 3 , E A x = 0 \boldsymbol{A x}=\mathbf{0} Ax = 0 A B = E \boldsymbol{A B}=\boldsymbol{E} AB = E B \boldsymbol{B} B
(20) 解 (I ) 对矩阵 A 作初等行变换, 有A = ( 1 − 2 3 − 4 0 1 − 1 1 1 2 0 − 3 ) → ( 1 0 0 1 0 1 0 − 2 0 0 1 − 3 ) , \displaystyle \begin{aligned} & \boldsymbol{A}=\left(\begin{array}{cccc}1 & -2 & 3 & -4 \\0 & 1 & -1 & 1 \\1 & 2 & 0 & -3\end{array}\right) \rightarrow\left(\begin{array}{cccc}1 & 0 & 0 & 1 \\0 & 1 & 0 & -2 \\0 & 0 & 1 & -3\end{array}\right), \end{aligned} A = 1 0 1 − 2 1 2 3 − 1 0 − 4 1 − 3 → 1 0 0 0 1 0 0 0 1 1 − 2 − 3 , 解系为 α = ( − 1 2 3 1 ) . \displaystyle \begin{aligned} \text { 解系为 } \boldsymbol{\alpha}=\left(\begin{array}{c}-1 \\2 \\3 \\1\end{array}\right) . \end{aligned} 解系为 α = − 1 2 3 1 . A x = 0 \boldsymbol{A x}=\mathbf{0} Ax = 0 α = ( − 1 2 3 1 ) \displaystyle \boldsymbol{\alpha}=\left(\begin{array}{c}-1 \\ 2 \\ 3 \\ 1\end{array}\right) α = − 1 2 3 1 ( A : E ) (\boldsymbol{A}: \boldsymbol{E}) ( A : E ) ( A : E ) = ( 1 − 2 3 − 4 1 0 0 0 1 − 1 1 0 1 0 1 2 0 − 3 0 0 1 ) → ( 1 0 0 1 2 6 − 1 0 1 0 − 2 − 1 − 3 1 0 0 1 − 3 − 1 − 4 1 ) . \displaystyle (\boldsymbol{A}: \boldsymbol{E})=\left(\begin{array}{cccc:ccc}1 & -2 & 3 & -4 & 1 & 0 & 0 \\0 & 1 & -1 & 1 & 0 & 1 & 0 \\1 & 2 & 0 & -3 & 0 & 0 & 1\end{array}\right) \rightarrow\left(\begin{array}{cccc:ccc}1 & 0 & 0 & 1 & 2 & 6 & -1 \\0 & 1 & 0 & -2 & -1 & -3 & 1 \\0 & 0 & 1 & -3 & -1 & -4 & 1\end{array}\right) . ( A : E ) = 1 0 1 − 2 1 2 3 − 1 0 − 4 1 − 3 1 0 0 0 1 0 0 0 1 → 1 0 0 0 1 0 0 0 1 1 − 2 − 3 2 − 1 − 1 6 − 3 − 4 − 1 1 1 . E = ( e 1 , e 2 , e 3 ) E=\left(e_1, e_2, e_3\right) E = ( e 1 , e 2 , e 3 ) A x = e 1 \boldsymbol{A} \boldsymbol{x}=\boldsymbol{e}_1 A x = e 1 x = ( 2 − 1 − 1 0 ) + k 1 α \displaystyle \boldsymbol{x}=\left(\begin{array}{c}2 \\ -1 \\ -1 \\ 0\end{array}\right)+k_1 \boldsymbol{\alpha} x = 2 − 1 − 1 0 + k 1 α k 1 k_1 k 1 A x = e 2 \boldsymbol{A x}=\boldsymbol{e}_2 Ax = e 2 x = ( 6 − 3 − 4 0 ) + k 2 α \displaystyle \boldsymbol{x}=\left(\begin{array}{c}6 \\ -3 \\ -4 \\ 0\end{array}\right)+k_2 \boldsymbol{\alpha} x = 6 − 3 − 4 0 + k 2 α k 2 k_2 k 2 A x = e 3 \boldsymbol{A x}=\boldsymbol{e}_3 Ax = e 3 x = ( − 1 1 1 0 ) + k 3 α \displaystyle \boldsymbol{x}=\left(\begin{array}{c}-1 \\ 1 \\ 1 \\ 0\end{array}\right)+k_3 \boldsymbol{\alpha} x = − 1 1 1 0 + k 3 α k 3 k_3 k 3 B = ( 2 6 − 1 − 1 − 3 1 − 1 − 4 1 0 0 0 ) + ( k 1 α , k 2 α , k 3 α ) , 其中 k 1 , k 2 , k 3 为任意常数. \displaystyle \boldsymbol{B}=\left(\begin{array}{ccc}2 & 6 & -1 \\-1 & -3 & 1 \\-1 & -4 & 1 \\0 & 0 & 0\end{array}\right)+\left(k_1 \boldsymbol{\alpha}, k_2 \boldsymbol{\alpha}, k_3 \boldsymbol{\alpha}\right) \text {, 其中 } k_1, k_2, k_3 \text { 为任意常数. } B = 2 − 1 − 1 0 6 − 3 − 4 0 − 1 1 1 0 + ( k 1 α , k 2 α , k 3 α ) , 其中 k 1 , k 2 , k 3 为任意常数 . (21) (本题满分 11 分)证明 n n n ( 1 1 ⋯ 1 1 1 ⋯ 1 ⋮ ⋮ ⋮ 1 1 ⋯ 1 ) \displaystyle \left(\begin{array}{cccc}1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & & \vdots \\ 1 & 1 & \cdots & 1\end{array}\right) 1 1 ⋮ 1 1 1 ⋮ 1 ⋯ ⋯ ⋯ 1 1 ⋮ 1 ( 0 ⋯ 0 1 0 ⋯ 0 2 ⋮ ⋮ ⋮ 0 ⋯ 0 n ) \displaystyle \left(\begin{array}{cccc}0 & \cdots & 0 & 1 \\ 0 & \cdots & 0 & 2 \\ \vdots & & \vdots & \vdots \\ 0 & \cdots & 0 & n\end{array}\right) 0 0 ⋮ 0 ⋯ ⋯ ⋯ 0 0 ⋮ 0 1 2 ⋮ n
(21) 证 设 A = ( 1 1 ⋯ 1 1 1 ⋯ 1 ⋮ ⋮ ⋮ 1 1 ⋯ 1 ) , B = ( 0 ⋯ 0 1 0 ⋯ 0 2 ⋮ ⋮ ⋮ 0 ⋯ 0 n ) \displaystyle \boldsymbol{A}=\left(\begin{array}{cccc}1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & & \vdots \\ 1 & 1 & \cdots & 1\end{array}\right), \boldsymbol{B}=\left(\begin{array}{cccc}0 & \cdots & 0 & 1 \\ 0 & \cdots & 0 & 2 \\ \vdots & & \vdots & \vdots \\ 0 & \cdots & 0 & n\end{array}\right) A = 1 1 ⋮ 1 1 1 ⋮ 1 ⋯ ⋯ ⋯ 1 1 ⋮ 1 , B = 0 0 ⋮ 0 ⋯ ⋯ ⋯ 0 0 ⋮ 0 1 2 ⋮ n ∣ λ E − A ∣ = ∣ λ − 1 − 1 ⋯ − 1 − 1 λ − 1 ⋯ − 1 ⋮ ⋮ ⋮ − 1 − 1 ⋯ λ − 1 ∣ = ( λ − n ) λ n − 1 , \displaystyle \begin{aligned} & |\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{cccc}\lambda-1 & -1 & \cdots & -1 \\-1 & \lambda-1 & \cdots & -1 \\\vdots & \vdots & & \vdots \\-1 & -1 & \cdots & \lambda-1\end{array}\right|=(\lambda-n) \lambda^{n-1}, \end{aligned} ∣ λ E − A ∣ = λ − 1 − 1 ⋮ − 1 − 1 λ − 1 ⋮ − 1 ⋯ ⋯ ⋯ − 1 − 1 ⋮ λ − 1 = ( λ − n ) λ n − 1 , ∣ λ E − B ∣ = ∣ λ 0 ⋯ − 1 0 λ ⋯ − 2 ⋮ ⋮ ⋮ 0 0 ⋯ λ − n ∣ = ( λ − n ) λ n − 1 , \displaystyle \begin{aligned} |\lambda \boldsymbol{E}-\boldsymbol{B}|=\left|\begin{array}{cccc}\lambda & 0 & \cdots & -1 \\0 & \lambda & \cdots & -2 \\\vdots & \vdots & & \vdots \\0 & 0 & \cdots & \lambda-n\end{array}\right|=(\lambda-n) \lambda^{n-1}, \end{aligned} ∣ λ E − B ∣ = λ 0 ⋮ 0 0 λ ⋮ 0 ⋯ ⋯ ⋯ − 1 − 2 ⋮ λ − n = ( λ − n ) λ n − 1 , A \boldsymbol{A} A B \boldsymbol{B} B λ 1 = n , λ 2 = 0 \lambda_1=n, \lambda_2=0 λ 1 = n , λ 2 = 0 n − 1 n-1 n − 1 A \boldsymbol{A} A A \boldsymbol{A} A Λ = ( n 0 ⋱ 0 ) . \displaystyle \boldsymbol{\Lambda}=\left(\begin{array}{llll}n & & & \\& 0 & & \\& & \ddots & \\& & & 0\end{array}\right) . Λ = n 0 ⋱ 0 . r ( λ 2 E − B ) = r ( B ) = 1 r\left(\lambda_2 \boldsymbol{E}-\boldsymbol{B}\right)=r(\boldsymbol{B})=1 r ( λ 2 E − B ) = r ( B ) = 1 B \boldsymbol{B} B λ 2 = 0 \lambda_2=0 λ 2 = 0 n − 1 n-1 n − 1 B \boldsymbol{B} B Λ \boldsymbol{\Lambda} Λ A \boldsymbol{A} A B \boldsymbol{B} B A \boldsymbol{A} A B \boldsymbol{B} B r ( A ) = r ( B ) = 1 r(\boldsymbol{A})=r(\boldsymbol{B})=1 r ( A ) = r ( B ) = 1 A \boldsymbol{A} A B \boldsymbol{B} B P \boldsymbol{P} P P T A P = B \boldsymbol{P}^{\mathrm{T}} \boldsymbol{A P}=\boldsymbol{B} P T AP = B (22) (本题满分 11 分)设随机变量 X X X P { X = 1 } = P { X = 2 } = 1 2 P\{X=1\}=P\{X=2\}=\frac{1}{2} P { X = 1 } = P { X = 2 } = 2 1 X = i X=i X = i Y Y Y U ( 0 , i ) ( i = 1 , 2 ) U(0, i)(i=1,2) U ( 0 , i ) ( i = 1 , 2 ) Y Y Y F Y ( y ) F_{Y}(y) F Y ( y ) E ( Y ) E(Y) E ( Y )
(22) (I) 求 Y Y Y F Y ( y ) F_{Y}(y) F Y ( y )
计算分布函数(三件套) F Y ( y ) = P { Y ⩽ y } F_Y(y) = P\{Y \leqslant y\} F Y ( y ) = P { Y ⩽ y } = 对离散的全集分解 P { Y ⩽ y , X = 1 } + P { Y ⩽ y , X = 2 } \xlongequal[]{\text{对离散的全集分解}}P\{Y \leqslant y ,X=1\} + P\{Y \leqslant y , X=2\} 对离散的全集分解 P { Y ⩽ y , X = 1 } + P { Y ⩽ y , X = 2 } = 独立 P { Y ⩽ y } \cdotp P { X = 1 } + P { Y ⩽ y } \cdotp P { X = 2 } \xlongequal[]{\text{独立}}P\{Y \leqslant y \}\text{·}P\{X=1\} +P\{Y \leqslant y \}\text{·}P\{X=2\} 独立 P { Y ⩽ y } \cdotp P { X = 1 } + P { Y ⩽ y } \cdotp P { X = 2 } = 转化 1 2 ∫ − ∞ y f Y ∣ X ( y ∣ 1 ) d y + 1 2 ∫ − ∞ y f Y ∣ X ( y ∣ 2 ) d y . \displaystyle \xlongequal[]{\text{转化}}\frac{1}{2} \int_{-\infty}^y f_{Y \mid X}(y \mid 1) \mathrm{d} y+\frac{1}{2} \int_{-\infty}^y f_{Y \mid X}(y \mid 2) \mathrm{d} y . 转化 2 1 ∫ − ∞ y f Y ∣ X ( y ∣ 1 ) d y + 2 1 ∫ − ∞ y f Y ∣ X ( y ∣ 2 ) d y . 随机发量 Y Y Y U ( 0 , i ) ( i = 1 , 2 ) U(0, i)(i=1,2) U ( 0 , i ) ( i = 1 , 2 ) 概率密度f ( x ) = { 1 b − a , a < x < b 0 , 其他 \displaystyle f(x)=\left\{\begin{array}{cl}\frac{1}{b-a}, & a<x<b \\ 0, & \text { 其他 }\end{array}\right. f ( x ) = { b − a 1 , 0 , a < x < b 其他 当 X = 1 X=1 X = 1 f Y ∣ X ( y ∣ 1 ) = { 1 , 0 < y < 1 , 0 , 其他. \displaystyle f_{Y \mid X}(y \mid 1)=\left\{\begin{array}{ll}1, & 0<y<1, \\ 0, & \text { 其他. }\end{array}\right. f Y ∣ X ( y ∣ 1 ) = { 1 , 0 , 0 < y < 1 , 其他 . X = 2 X=2 X = 2 f Y ∣ X ( y ∣ 2 ) = { 1 2 , 0 < y < 2 , 0 , 其他. \displaystyle f_{Y \mid X}(y \mid 2)=\left\{\begin{array}{ll}\frac{1}{2}, & 0<y<2, \\ 0, & \text { 其他. }\end{array}\right. f Y ∣ X ( y ∣ 2 ) = { 2 1 , 0 , 0 < y < 2 , 其他 . 画图 根据 y y y 当 y < 0 y < 0 y < 0 F Y ( y ) = 0 F_Y(y) = 0 F Y ( y ) = 0 当 0 ⩽ y < 1 0 \leqslant y < 1 0 ⩽ y < 1 F Y ( y ) = 1 2 ∫ 0 y 1 d y + 1 2 ∫ 0 y 1 2 d y = 1 2 y + 1 4 y = 3 4 y \displaystyle \begin{aligned} F_Y(y) & =\frac{1}{2} \int_0^y1 \mathrm{~d} y+\frac{1}{2} \int_0^y\frac{1}{2} \mathrm{~d} y =\frac{1}{2} y+\frac{1}{4} y=\frac{3}{4} y\end{aligned} F Y ( y ) = 2 1 ∫ 0 y 1 d y + 2 1 ∫ 0 y 2 1 d y = 2 1 y + 4 1 y = 4 3 y 当 1 ⩽ y < 2 1 \leqslant y < 2 1 ⩽ y < 2 F Y ( y ) = 1 2 ∫ 0 1 1 d y + 1 2 ∫ 0 y 1 2 d y = 1 2 × 1 + 1 4 y = 1 2 + 1 4 y \displaystyle \begin{aligned} F_Y(y) & =\frac{1}{2} \int_0^1 1 \mathrm{~d} y+\frac{1}{2} \int_0^y \frac{1}{2} \mathrm{~d} y =\frac{1}{2} \times 1+\frac{1}{4} y=\frac{1}{2}+\frac{1}{4} y\end{aligned} F Y ( y ) = 2 1 ∫ 0 1 1 d y + 2 1 ∫ 0 y 2 1 d y = 2 1 × 1 + 4 1 y = 2 1 + 4 1 y 当 y ⩾ 2 y \geqslant 2 y ⩾ 2 F Y ( y ) = 1 F_Y(y) = 1 F Y ( y ) = 1 Y的分布函数为:F Y ( y ) = { 0 , y < 0 , 3 4 y , 0 ⩽ y < 1 , 1 2 + 1 4 y , 1 ⩽ y < 2 , 1 , y ⩾ 2 \displaystyle F_Y(y)=\left\{\begin{array}{ll}0, & y<0, \\ \frac{3}{4} y, & 0 \leqslant y<1, \\ \frac{1}{2}+\frac{1}{4} y, & 1 \leqslant y<2, \\ 1, & y \geqslant 2\end{array}\right. F Y ( y ) = ⎩ ⎨ ⎧ 0 , 4 3 y , 2 1 + 4 1 y , 1 , y < 0 , 0 ⩽ y < 1 , 1 ⩽ y < 2 , y ⩾ 2 E ( Y ) E(Y) E ( Y ) 计算 Y Y Y f Y ( y ) = F Y ′ ( y ) = { 3 4 , 0 < y < 1 , 1 4 , 1 < y < 2 , 0 , 其他 \displaystyle f_Y(y) = F_Y^{\prime}(y) = \begin{cases} \frac{3}{4}, & 0 < y < 1, \\ \frac{1}{4}, & 1 < y < 2, \\ 0, & \text{其他} \end{cases} f Y ( y ) = F Y ′ ( y ) = ⎩ ⎨ ⎧ 4 3 , 4 1 , 0 , 0 < y < 1 , 1 < y < 2 , 其他 计算 E ( Y ) E(Y) E ( Y ) E ( Y ) = ∫ − ∞ + ∞ y f Y ( y ) d y = 分段积分 ∫ 0 1 3 4 y d y + ∫ 1 2 1 4 y d y = 3 4 \displaystyle E(Y) = \int_{-\infty}^{+\infty} y f_Y(y) dy\xlongequal[]{\text{分段积分}}\int_0^1 \frac{3}{4} y dy + \int_1^2 \frac{1}{4} y dy= \frac{3}{4} E ( Y ) = ∫ − ∞ + ∞ y f Y ( y ) d y 分段积分 ∫ 0 1 4 3 y d y + ∫ 1 2 4 1 y d y = 4 3 总结,Y Y Y F Y ( y ) = { 0 , y < 0 , 3 y 4 , 0 ⩽ y < 1 , 1 2 + y 4 , 1 ⩽ y < 2 , 1 , y ⩾ 2 \displaystyle F_Y(y) = \begin{cases}0, & y < 0, \\ \frac{3y}{4}, & 0 \leqslant y < 1, \\ \frac{1}{2} + \frac{y}{4}, & 1 \leqslant y < 2, \\ 1, & y \geqslant 2 \end{cases} F Y ( y ) = ⎩ ⎨ ⎧ 0 , 4 3 y , 2 1 + 4 y , 1 , y < 0 , 0 ⩽ y < 1 , 1 ⩽ y < 2 , y ⩾ 2 E ( Y ) = 3 4 E(Y) = \frac{3}{4} E ( Y ) = 4 3 (23) (本题满分 11 分)X X X F ( x ; θ ) = { 1 − e − x 2 θ , x ⩾ 0 , 0 , x < 0 , \displaystyle F(x ; \theta)=\left\{\begin{array}{ll}1-\mathrm{e}^{-\frac{x^{2}}{\theta},} & x \geqslant 0, \\ 0, & x<0,\end{array}\right. F ( x ; θ ) = { 1 − e − θ x 2 , 0 , x ⩾ 0 , x < 0 , θ \theta θ X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n X X X E ( X ) E(X) E ( X ) E ( X 2 ) E\left(X^{2}\right) E ( X 2 ) θ \theta θ θ ^ n \widehat{\theta}_{n} θ n a a a ε > 0 \varepsilon>0 ε > 0 lim n → ∞ P { ∣ θ ^ n − a ∣ ⩾ ε } = 0 \displaystyle \lim _{n \rightarrow \infty} P\left\{\left|\widehat{\theta}_{n}-a\right| \geqslant \varepsilon\right\}=0 n → ∞ lim P { θ n − a ⩾ ε } = 0
(23) (I ) 总体 X X X f ( x ; θ ) = { 2 x θ e − x 2 θ , x > 0 , 0 , 其他. \displaystyle f(x ; \theta)= \begin{cases}\frac{2 x}{\theta} \mathrm{e}^{-\frac{x^2}{\theta}}, & x>0, \\ 0, & \text { 其他. }\end{cases} f ( x ; θ ) = { θ 2 x e − θ x 2 , 0 , x > 0 , 其他 . E X = ∫ 0 + ∞ x ⋅ 2 x θ e − x 2 θ d x = − ∫ 0 + ∞ x d ( e − x 2 θ ) = ∫ 0 + ∞ e − x 2 θ d x \displaystyle \begin{aligned} E X=\int_0^{+\infty} x \cdot \frac{2 x}{\theta} \mathrm{e}^{-\frac{x^2}{\theta}} \mathrm{d} x=-\int_0^{+\infty} x \mathrm{~d}\left(\mathrm{e}^{-\frac{x^2}{\theta}}\right)=\int_0^{+\infty} \mathrm{e}^{-\frac{x^2}{\theta}} \mathrm{d} x\end{aligned} EX = ∫ 0 + ∞ x ⋅ θ 2 x e − θ x 2 d x = − ∫ 0 + ∞ x d ( e − θ x 2 ) = ∫ 0 + ∞ e − θ x 2 d x = π θ 2 ⋅ 1 π θ ∫ − ∞ + ∞ e − x 2 θ d x = π θ 2 , \displaystyle \begin{aligned}=\frac{\sqrt{\pi \theta}}{2} \cdot \frac{1}{\sqrt{\pi \theta}} \int_{-\infty}^{+\infty} \mathrm{e}^{-\frac{x^2}{\theta}} \mathrm{d} x=\frac{\sqrt{\pi \theta}}{2},\end{aligned} = 2 π θ ⋅ π θ 1 ∫ − ∞ + ∞ e − θ x 2 d x = 2 π θ , E ( X 2 ) = ∫ 0 + ∞ x 2 ⋅ 2 x θ e − x 2 θ d x = θ ∫ 0 + ∞ u e − u d u = θ . \displaystyle \begin{aligned} E\left(X^2\right)=\int_0^{+\infty} x^2 \cdot \frac{2 x}{\theta} \mathrm{e}^{-\frac{x^2}{\theta}} \mathrm{d} x=\theta \int_0^{+\infty} u \mathrm{e}^{-u} \mathrm{~d} u=\theta . \end{aligned} E ( X 2 ) = ∫ 0 + ∞ x 2 ⋅ θ 2 x e − θ x 2 d x = θ ∫ 0 + ∞ u e − u d u = θ . 陷阱:题中给出的是分布函数,因此需要求导得到概率密度 总体 X X X f ( x ; θ ) = { 2 x θ e − x 2 θ , x ≥ 0 0 , 其他 \displaystyle f(x ; \theta)=\left\{\begin{array}{ll}\frac{2 x}{\theta} e^{-\frac{x^{2}}{\theta}}, & x \geq 0 \\ 0, & \text{其他}\end{array}\right. f ( x ; θ ) = { θ 2 x e − θ x 2 , 0 , x ≥ 0 其他 设 x 1 , x 2 , ⋯ x n x_{1}, x_{2}, \cdots x_{n} x 1 , x 2 , ⋯ x n 写出似然函数: L ( θ ) = ∏ i = 1 n f ( x i ) = { 2 n θ n \cdotp x 1 x 2 ⋯ x n \cdotp e − 1 θ ∑ i = 1 n x i 2 ⏞ 将 θ 当做系数提出来 ⏟ 三项相乘 x 1 , x 2 , ⋯ x n > 0 0 , \displaystyle L(\theta)=\prod_{i=1}^{n} f\left(x_{i}\right)=\left\{\begin{array}{cc}\underbrace{\frac{2^{n} }{\theta^{n}} \text{·}x_{1} x_{2} \cdots x_{n}\text{·}\overbrace{e^{-\frac{1}{\theta} \sum_{i=1}^{n} x_{i}^{2}}}^{\text{将}\theta\text{当做系数提出来}}}_{\text{三项相乘}}& x_{1}, x_{2}, \cdots x_{n}>0 \\ 0, & \end{array}\right. L ( θ ) = i = 1 ∏ n f ( x i ) = ⎩ ⎨ ⎧ 三项相乘 θ n 2 n \cdotp x 1 x 2 ⋯ x n \cdotp e − θ 1 ∑ i = 1 n x i 2 将 θ 当做系数提出来 0 , x 1 , x 2 , ⋯ x n > 0 取对数:ln L ( θ ) = − n ln θ + ln 2 n + ln ( ∑ i = 1 n x i ) − 1 θ ∑ i = 1 n x i 2 \displaystyle \ln L(\theta)=-n \ln \theta+\ln 2^n+\ln \left(\sum_{i=1}^n x_i\right)-\frac{1}{\theta} \sum_{i=1}^n x_i^2 ln L ( θ ) = − n ln θ + ln 2 n + ln ( i = 1 ∑ n x i ) − θ 1 i = 1 ∑ n x i 2 对θ \theta θ d ( 1 + L ( θ ) d θ = − n θ + ∑ i = 1 n x i 2 1 θ 2 = 0 \displaystyle \frac{d(1+L(\theta)}{d \theta}=-\frac{n}{\theta}+\sum_{i=1}^n x_i^2 \frac{1}{\theta^2}=0 d θ d ( 1 + L ( θ ) = − θ n + i = 1 ∑ n x i 2 θ 2 1 = 0 移项得 θ \theta θ θ ^ n = 1 n ∑ i = 1 n x i 2 \displaystyle \hat{\theta}_{n}=\frac{1}{n} \sum_{i=1}^{n} x_{i}^{2} θ ^ n = n 1 i = 1 ∑ n x i 2 从而 θ \theta θ θ n ^ = 1 n ∑ i = 1 n X i 2 \displaystyle \widehat{\theta_{n}}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{2} θ n = n 1 i = 1 ∑ n X i 2 a = θ a=\theta a = θ { X n 2 } \left\{X_n^2\right\} { X n 2 } E ( X 1 2 ) = θ < + ∞ E\left(X_1^2\right)=\theta<+\infty E ( X 1 2 ) = θ < + ∞ n → ∞ n \rightarrow \infty n → ∞ θ ^ n = 1 n ∑ i = 1 n X i 2 \displaystyle \hat{\theta}_n=\frac{1}{n} \sum_{i=1}^n X_i^2 θ ^ n = n 1 i = 1 ∑ n X i 2 E ( X 1 2 ) E\left(X_1^2\right) E ( X 1 2 ) θ \theta θ ε > 0 \varepsilon>0 ε > 0 lim n → ∞ P { ∣ θ ^ n − θ ∣ ⩾ ε } = 0. \displaystyle \lim _{n \rightarrow \infty} P\left\{\left|\hat{\theta}_n-\theta\right| \geqslant \varepsilon\right\}=0 . n → ∞ lim P { θ ^ n − θ ⩾ ε } = 0. 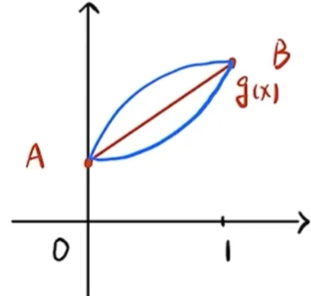
 ,
,