一、选择题
(本题共 8 小题, 每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有一项符合题目 要求, 把所选项前的字母填在题后的括号内. )
(1)
- 下列函数中, 在 x=0 处不可导的是 ()
(A) f(x)=∣x∣sin∣x∣.
(B) f(x)=∣x∣sin∣x∣.
(C) f(x)=cos∣x∣.
(D) f(x)=cos∣x∣.
(1)
- 答 应选(D).
- 解 按定义考查 f(x) 在 x=0 处的可导性, 即考查 x→0limxf(x)−f(0) 是否存在.
- 选项(A), x→0limxf(x)−f(0)=x→0limx∣x∣sin∣x∣=x→0limx∣x∣⋅∣x∣=0, 可导.
- 选项(B), x→0limxf(x)−f(0)=x→0limx∣x∣sin∣x∣=x→0limx∣x∣⋅∣x∣=0, 可导.
- 选项(C), x→0limxf(x)−f(0)=x→0limxcos∣x∣−1=x→0limx−21∣x∣2=0, 可导.
- 选项(D),
- x→0limxf(x)−f(0)=x→0limxcos∣x∣−1=x→0limx−21∣x∣
- 不存在.
- 因为 x→0+limx−21∣x∣=−21,x→0+limx−21∣x∣=21,f+′(0)=f−′(0), 所以 f′(0) 不存在. 因此选(D).
(2)
- 过点 (1,0,0),(0,1,0), 且与曲面 z=x2+y2 相切的平面为 ()
- (A) z=0 与 x+y−z=1.
- (B) z=0 与 2x+2y−z=2.
- (C) x=y 与 x+y−z=1.
- (D) x=y 与 2x+2y−z=2.
(2)
- 答 应选(B).
- 设所求平面与曲面 z=x2+y2 的切点为 (x0,y0,z0),
- 曲面 z=x2+y2 在切点 (x0,y0,z0) 的法向量 n=(2x0,2y0,−1),
- 故切平面方程为 2x0(x−x0)+2y0(y−y0)−(z−z0)=0, 这里 z0=x02+y02.
- 代入定点 (1,0,0) 和 (0,1,0) 到上述切平面方程中可得
(x0,y0,z0)=(0,0,0),(x0,y0,z0)=(1,1,2),
- 故切平面方程 为 z=0 与 2x+2y−z=2, 选 (B).
(3)
- n=0∑∞(−1)n(2n+1)!2n+3=()
- (A) sin1+cos1.
- (B) 2sin1+cos1.
- (C) 2sin1+2cos1.
- (D) 2sin1+3cos1.
(3)
- 答 应选 (B).
- 解 这是常数项级数的求和, 按该级数的特点与题目设置的选项, 提示我们要用分解法并结合 sinx 与 cosx 的算级数展开式求得该常数项级数的和.
- 已知 sinx=n=0∑∞(2n+1)!(−1)nx2n+1(∣x∣<+∞),cosx=n=0∑∞(2n)!(−1)nx2n(∣x∣<+∞),
- 现将原级数分解成
- n=0∑∞(−1)n(2n+1)!2n+3=n=0∑∞(−1)n(2n+1)!(2n+1)+2
- =n=0∑∞(2n)!(−1)n+2n=0∑∞(2n+1)!(−1)n=cos1+2sin1.
- 常见的初等函数的幂级数展开式
- ex=n=0∑∞n!1xn(−∞<x<+∞)
- sinx=n=0∑∞(2n+1)!(−1)nx2n+1(−∞<x<+∞)
- 1+x1=n=0∑∞(−1)nxn(−1<x<1),
- 1+x21=n=0∑∞(−1)nx2n(−1<x<1)
- ax=exlna=n=0∑∞n!(lna)nxn(−∞<x<+∞)
- cosx=n=0∑∞(2n)!(−1)nx2n(−∞<x<+∞)
- ln(1+x)=n=1∑∞n(−1)n−1xn(−1<x⩽1)
- arctanx=n=0∑∞2n+1(−1)nx2n+1(−1⩽x⩽1)
(4)
- 设 M=∫−2π2π1+x2(1+x)2 dx,N=∫−2π2πex1+x dx,K=∫−2π2π(1+cosx)dx, 则 ( )
- (A) M>N>K.
- (B) M>K>N.
- (C) K>M>N.
- (D) K>N>M.
(4)
- 问题: 比较 M,N,K 的大小,转化为仅比较被积函数的大小
- 第一步:比较 M与1的大小
- 化简过程:
- 根据对称区间联想到奇偶性:
M=∫−2π2π1+x2(1+x)2dx1+x21+x2+2x∫−222π1dx+∫−22221+x22xdxx为奇函数=0∫−2π2π1dx
- 化简结果: M=∫−2π2π1dx
- 第二步:比较K与1的大小
- 比较 1 和 1+cosxcosx>01<1+cosx
- 结论: M<K(排除选项 (A) 和 (B))
- 第三步:比较N与 1 的大小
- 令 f(x)=ex−x−1, 则 f′(x)=ex−1,f′′(x)=ex>0,
- 故该函数是凹函数,f(x)>f(0)=0
- 则f(x)=ex−x−1>0移项ex1+x<1
- 结果: N<M
- 整理得:ex1+x<1<1+cosx
- 由函数大,积分就大: N<M<K(选项 (C))
(5)
- 下列矩阵中, 与矩阵 100110011 相似的为 ( )
- (A) 100110−111.
- (B) 100010−111.
- (C) 100110−101.
- (D) 100010−101.
(5)
- 答 应选 (A).
- 解 设 A=100110011,A 和各选项中的矩阵都不相似于对角矩阵.
- 对这样的两个矩阵, 要判定它们相似需要大纲要求以外的知识, 而判定它们不相似是有办法的. 因此本题采用排除法.
- 由相似的矩阵相等, 知若 A 相似于 B, 则 A−E 相似于 B−E, 从而 r(A−E)=r(B−E).
- A−E=000100010,r(A−E)=2
- 而当 B 取 (B), (C), (D) 中的任一矩阵时, 都有 r(B−E)=1. 从而 (B),(C),(D) 都排除,故选 (A).
(6)
- 设 A,B 为 n 阶矩阵,记 r(X) 为矩阵 X 的秩, (X,Y) 表示分块矩阵,则 ( )
- (A) r(A,AB)=r(A).
- (B) r(A,BA)=r(A).
- (C) r(A,B)=max{r(A),r(B)}.
- (D) r(A,B)=r(AT,BT).
(6)
- 答 应选 (A).
- 解 一方面, A 是 (AAB) 的子矩阵, 因此 r(AAB)⩾r(A).
- 另一方面, (A AB) 是 A 与 (EB) 的乘积, 即 (AAB)=A(EB), 因此 r(AAB)⩽r(A), 故 r(AAB)=r(A).
(7)
- 设随机变量 X 的概率密度 f(x) 满足 f(1+x)=f(1−x), 且 ∫02f(x)dx=0.6, 则 P{X<0}=
- (A) 0.2 .
- (B) 0. 3 .
- (C) 0. 4 .
- (D) 0.5 .
(7)
- 分析概率密度 f(x) 的性质:
- f(1+x)=f(1−x),表示 f(x) 关于 x=1 对称。
- 由对称性可知,P{X<1}对称性0.5。
- 计算给定区间内的概率:
- 已知 ∫02f(x)dx=0.6,表示 P{0<X<2}=0.6。
- 根据对称性,P{0<X<1}对称性21P{0<X<2}=0.3。
- 合并后计算 P{X=1}概率计算P{X<1}−P{0<X<1}
- 具体值0.5−0.3=0.2
(8)
- 设总体 X 服从正态分布 N(μ,σ2).X1,X2,⋯,Xn 是来自总体 X 的简单随机样本,据此样本检验 假设 H0:μ=μ0,H1:μ=μ0, 则 ( )
- (A) 如果在检验水平 α=0.05 下拒绝 H0, 那么 α=0.01 下必拒绝 H0.
- (B) 如果在检验水平 α=0.05 下拒绝 H0, 那么 α=0.01 下必接受 H0.
- (C) 如果在检验水平 α=0.05 下接受 H0, 那么 α=0.01 下必拒绝 H0.
- (D) 如果在检验水平 α=0.05 下接受 H0, 那么 α=0.01 下必接受 H0.
(8)
- 解 已知方差 σ2 关于 μ 的检验所用统计量服从正态分布, 未知方差 σ2 关于 μ 的检验所用统计量服从 t 分布. 无论正态分布还是 t 分布, 拒绝域都随着显著性水平 α 的减小而减小. 相反, 接受域随着 α 的减小而 增大, 也就是说在 α=0.01 下的接受域包含了在 α=0.05 下的接受域, 若在 α=0.05 下 H0 被接受了, 则在 α=0.01 下 H0 必被接受, 故选(D).
二、填空题
(本题共 6 小题,每小题 4 分,共 24 分,把答案填在题中横线上. )
(9)
若 x→0lim(1+tanx1−tanx)sinkx1=e, 则 k=
(9)
- 使用 eln变形:转换为 e 的指数形式。
- exp(x→0limsinkxln(1+tanx1−tanx))=e
- 把指数单独拿出来算
- x→0limsinkxln(1+tanx1−tanx−1+1)
- ln(1+x−1)~x−1x→0limsinkx1(1+tanx1−tanx−1)
- 通分sinkx1(1+tanx1−tanx−1)=sinkx(1+tanx)−2tanx。
- 求极限:将x=0代入:x→0limsinkx(1+tanx)−2tanx=−k2。
(10)
设函数 f(x) 具有 2 阶连续导数. 若曲线 y=f(x) 过点 (0,0) 且与曲线 y=2x 在点 (1,2) 处相切, 则 ∫01xf′′(x)dx=
(10)
- 答 应填 2(ln2−1).
- 曲线 y=f(x) 过点 (0,0) 且与曲线 y=2x 在点 (1,2) 处相切
- 根据题设条件 f(0)=0,f(1)=21=2,f′(1)=(2x)′∣x=1=2ln2
- 使用积分的分部积分法计算 ∫01xf′′(x)dx
- ∫01xf′′(x)dx=∫01xd[f′(x)]
- ∫01xf′′(x)dx分布xf′(x)∣01−∫01f′(x)dx
- =f′(1)−f(x)∣01
- =f′(1)−f(1)+f(0)
- ∫01xf′′(x)dx=2ln2−2
- =2(ln2−1)
(11)
设 F(x,y,z)=xyi−yzj+zxk, 则 rotF(1,1,0)=
(11)
- 答 应填 i−k.
- 记三元向量函数 F(x,y,z)=(P,Q,R), 则类比斯托克斯
- rotF(x,y,z)=i∂x∂Pj∂y∂Qk∂z∂R,
- 这里 P=xy,Q=−yz,R=zx,
- 于是rotF(1,1,0)=ijk∂x∂∂y∂∂z∂xy−yzzx(1,1,0)
- 注意正负号[0−(−y)]i+(−1)⋅(z−0)j+(0−x)k
- =(yi−zj−xk)∣(1,1,0)=i−k
(12)
设 L 为球面 x2+y2+z2=1 与平面 x+y+z=0 的交线, 则 ∮Lxy ds=
(12)
- 由曲线 L 的方程可知,该曲线对变量 x,y,z 具有轮换对称性.
于是,∮Lxy ds=∮Lyz ds=∮Lzx ds=31∮L(xy+yz+zx)ds.- 并且 xy+yz+zx完全平方21[(x+y+z)2−(x2+y2+z2)]
- 所以∮Lxy ds=31∮L(xy+yz+zx)ds=61∮L[(x+y+z)2−(x2+y2+z2)]ds
- x+y+z=0x2+y2+z2=161∮L(0−1)ds=−61∮L ds.
- =−61×2π×1=−3π
- 由于 L 为单位球面上的一个大圆, 即以球心为圆心, 且半径等于球半径的一个圆,
- 故 ∮L ds=L 的周长 =2π×1=2π.
- 2007 年数一试题
设曲面 Σ:∣x∣+∣y∣+∣z∣=1,则 ∮Σ(x+∣y∣)dS= - 曲面 Σ 是一个以原点为中心的正八面体, 关于三个坐标面均对称, 且对变量 x,y,z 具有轮换对称性。
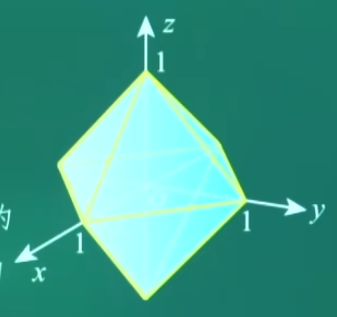
- 记 I=∬Σ(x+∣y∣)dS. 由于 Σ 关于 yOz 面对称,
- 而 x 是关于 x 的奇函数, 故 ∬Σx dS=0.
- 又因为 Σ 对变量 x,y,z 具有轮换对称性, 所以
- I=∬Σ∣y∣dS=31∬Σ(∣x∣+∣y∣+∣z∣)dS=31∬ΣdS=31⋅Σ 的面积.
- Σ 的每个面是边长为 2 的正三角形, 面积为 21×(2)2×23=23, 从而 Σ 的面积为 8×23= 43.
- 因此, I=343.
- 2009 年数一试题
设 Ω={(x,y,z)∣x2+y2+z2≤1}, 则 ∭Ωz2 dx dy dz= - 2015 年数一试题
设 Ω 是由平面 x+y+z=1 与三个坐标平面所围成的空间区域, 则 ∭Ω(x+2y+3z)dx dy dz=
(13)
设 2 阶矩阵 A 有两个不同特征值, α1,α2 是 A 的线性无关的特征向量, 且满足 A2(α1+α2)= α1+α2, 则 ∣A∣=
(13)
- 分析 本题主要考查特征值与特征向量的概念,以及矩阵的行列式与其特征值之间的关系.
- 行列式与特征值的关系: ∣A∣=∏i=1nλi ,其中 λi(i=1,2,⋯,n) 是 n 阶矩阵 A 的特征值.
- 答 应填一 1 .
(14)
设随机事件 A 与 B 相互独立, A 与 C 相互独立, BC=∅. 若 P(A)=P(B)=21,P(AC∣AB∪C)=41, 则 P(C)=
(14)
- 读题
- A 与 B 相互独立,得P(AB)=P(A)⋅P(B)=41
- A 与 C 相互独立,得P(AC)=P(A)P(C)
- BC=∅,得P(BC)=P(ABC)=0
- 计算 条件概率公式:P(AC∣AB∪C)=P(AB∪C)P(AC(AB∪C))
- 展开分子:P(AC(AB∪C))=P(ABC∪AC)P(ABC)=0P(AC)独立P(A)P(C)=21P(C)
- 展开分母: P(AB∪C)=P(AB)+P(C)−=0P(ABC)=41+P(C)
- 原式P(AC∣AB∪C)=41=41+P(C)21P(C)
- 161+41P(C)=21P(C)
- 解方程找到 P(C)=41
gpt版
- 首先分析给定的事件的独立性和互斥性:
- A 与 B 相互独立,得 P(AB)=P(A)⋅P(B)=41
- A 与 C 相互独立,得 P(AC)=P(A)⋅P(C)
- BC=∅,得 P(BC)=0(即 B 和 C 互斥)
- 接下来,计算条件概率 P(AC∣AB∪C):
- 根据条件概率公式:P(AC∣AB∪C)=P(AB∪C)P(AC∩(AB∪C))
- 展开分子:
- P(AC∩(AB∪C))=P(ACB∪AC)
- P(ACB)=0P(AC)
- A 和 C 独立P(A)P(C)=21P(C)
- 展开分母:
- P(AB∪C)=P(AB)+P(C)−=0P(ABC)
- =41+P(C)
- 将分子和分母代入条件概率公式:
- 41=41+P(C)21P(C)
- 解方程得 P(C)=41
(15)
(本题满分 10 分) 求不定积分 ∫e2xarctanex−1 dx.
(15)
分部积分准备: ∫udv=uv−∫vdu
- 选择 u=arctanex−1 ,
- 选择v=e2x
- 原式=21∫arctanex−1d(e2x)
- =21e2xarctanex−1−21∫e2xd[arctanex−1]
- [arctanex−1]′=(arctanex−1)′1+ex−11\cdotp(ex−1))′21ex−11\cdotp(ex−1)′ex=21ex−11dx
- =21e2xarctanex−1−21∫ex−1e2xdx
- (法一)令 t=ex, 则 dt=ex dx.
- ∫ex−1e2x dx=∫ex−1ex d(ex)
- =∫t−1t dt=∫t−1t−1+1 dt=∫(t−1+t−11)dt
- =32(t−1)23+2t−1+C1
- =32(ex−1)23+2ex−1+C1
- =21e2xarctanex−1−21ex−1−61(ex−1)23+C.
方法2
- 换元法准备: 令 t=ex−1
- e2x=(1+t2)2
- x=ln(1+t2),dx=1+t22tdt
- 应用换元法: ∫ex−1e2xdx=∫t(1+t2)2⋅1+t22tdt=2⋅∫(1+t2)dt=2⋅(t+3t3)dt
- 将t=ex−1带回:=2ex−1+32(ex−1)23dx
(16)
(本题满分 10 分) 将长为 2 m 的铁丝分成三段,依次围成圆、正方形与正三角形. 三个图形的面积之和是否存在最小值?若存在,求出最小值.
(16)
- 圆的半径为 x,正方形的边长为 y,正三角形的边长为 z。
- 面积函数 f(x,y,z)=πx2+y2+43z2。
- 约束条件为周长 2πx+4y+3z=2
- 构造拉格朗日函数 L(x,y,z,λ)。
- L(x,y,z,λ)=πx2+y2+43z2+λ(2πx+4y+3z−2)。
- 求解边界上的驻点
- 对 L(x,y,z,λ) 求偏导数,设置为零。
- ∂x∂L=2πx+2πλ。
- ∂y∂L=2y+4λ。
- ∂z∂L=23z+3λ
- ∂λ∂L=2πx+4y+3z−2。
- 代入消元法解得驻点 x0,y0,z0,不用求λ,λ是用来消元的
- x0=π+4+331。
- y0=π+4+332。
- z0=π+4+3323。
- 计算最小值,将驻点代入 f(x,y,z)
- 最小面积 f(x0,y0,z0)=πx2+y2+43z2=π+4+331
(17)
(本题满分 10 分) 设 Σ 是曲面 x=1−3y2−3z2 的前侧, 计算曲面积分 I=∬Σx dy dz+(y3+2)dz dx+z3 dx dy.
(17)
- 解题思路:补面用高斯,补的面:积分为零,补的面是一个平面
- 曲面 Σ 为位于 yOz 面前侧的半个椭球面的前侧, 椭球面方程为 x2+3y2+3z2=1.
Σ不是封闭曲面, 可以先添加辅助曲面,再利用高斯公式将所求第二类曲面积分转化为三重积分进行计算. - 高斯公式:设空间闭区域 Ω 由分片光滑的闭曲面 Σ 所围成. 若函数 P(x,y,z),Q(x,y,z),R(x,y,z) 在 Ω 上具有一阶连续偏导数,则有
∭Ω(∂x∂P+∂y∂Q+∂z∂R)dv=∬ΣP dy dz+Q dz dx+R dx dy,
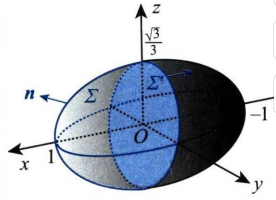
- (解) 如图所示, 添加辅助平面 Σ′:x=0x2+3y2+3z2=1取x=0,代入上式(3y2+3z2⩽1), 取后侧,
即法向量指向 x 轴负向, 则 Σ与 Σ′ 围成一个半椭球体 Ω, 且法向量指向外侧. - I=∬Σ+Σ′x dy dz+(y3+2)dz dx+z3 dx dy−=0,补的平面积分为零∬Σ′x dy dz+(y3+2)dz dx+z3 dx dy.
- =∬Σ+Σ′′′x dy dz+(y3+2)dz dx+z3 dx dy高斯∭Ω′′(1+3y2+3z2)dv.
柱线法
- 采用先重后单的积分次序计算 ∭Ω(1+3y2+3z2)dv.
沿平行于 yOz 面的方向作 Ω 的横截面,得Dx={(y,z)∣3y2+3z2⩽1−x2}.- Dx 是半径为 31−x2 的圆盘. 于是,Ω={(x,y,z)∣(y,z)∈Dx,0⩽x⩽1}.
- {(r,θ)0≤r≤31−x2,0≤θ≤2π}
- ∭Ω(1+3y2+3z2)dv=∫01 dx∬Dx(1+3y2+3z2)dy dz
- 极坐标 ∫01 dx∫02π dθ∫031−x2(1+3r2)⋅r dr
- =2π∫01(2r2+43r4)031−x2 dx
- =2π∫01[61−x2+43⋅32(1−x2)2]dx
- =6π∫01(x4−4x2+3)dx.
- =6π×(51−34+3)=4514π
转换投影法
- Σ′:z=I1−3y2−3x2
- I=∬Σ′zdydx+(y3+2)dxdz+x3dydz
- 重新排序∬Σ′x3dydz+(y3+2)dxdz+zdxdy
这道题用转换投影法不好算,因为被积函数很复杂
截面法
- 2007 年数一试题计算曲面积分
I=∬Σxz dy dz+2zy dz dx+3xy dx dy,其中 Σ 为曲面 z=1−x2−4y2(0≤z≤1) 的上侧. - 2008 年数一试题
设曲面 Σ 是 z=4−x2−y2 的上侧, 则 ∬Ξxy dy dz+x dz dx+x2 dx dy=
(18)
(本题满分 10 分) 已知微分方程 y′+y=f(x), 其中 f(x) 是 R 上的连续函数.
(I) 若 f(x)=x, 求方程的通解;
(II) 若 f(x) 是周期为 T 的函数, 证明: 方程存在唯一的以 T 为周期的解.
(18)
- (I) 解
- 当 f(x)=x 时,方程化为 y′+y=x,是一阶线性微分方程
- 通解为y=e−x(C1+∫xex dx)=e−x(C1+xex−ex)
- =C1e−x+x−1(C1 为任意常数 ).
(19)
(本题满分 10 分)
设数列 {xn} 满足: x1>0,xnexn+1=exn−1(n=1,2,⋯). 证明 {xn} 收敛, 并求 n→∞limxn.
(19)
- 第一步:证明数列收敛
- 分析和证明过程:
- 证0<x2<x1
- 观察到 1=e0,可以对原式运用拉格朗日中值定理,存在ξ属于0<ξ<x1:
ex2=x1ex1−11=e0x1−0ex1−e0拉格朗日x1eξ⋅(x1−0)分子分母消去1eξ
其中 ,x2=ξ,这样,0<x2<x1。
- 假设 0<xn<xn−1,接下来证明 0<xn+1<xn:
exn+1=xnexn−11=e0xnexn−e0拉格朗日xneη⋅(xn−0)=eη- 其中 0<η<xn,因此 xn+1=η,得出 0<xn+1<xn。
- 结论:数列 {xn} 单调递减,且有下界 0,因此收敛。
- 第二步:求出数列的极限
- 极限求解过程:
- 设 n→∞limxn=a。
- 对 xnexn+1=exn−1 两边取极限:aea=ea−1
- 考虑函数 f(x)=xex−ex+1
- 其导数x>0,ex>0, f′(x)=xex>0,所以函数单调增。
- 由{f′(x)>0f(0)=0所以 a=0 是 aea=ea−1 的唯一实根。
- 结论:n→∞limxn=0。
- 数列 {xn} 单调递减且有下界,故收敛。
- 极限 n→∞limxn=0 是通过求解方程 aea=ea−1 得出的,使用函数的单调性来证明这是唯一解。
(20)
(本题满分 11 分)
设实二次型 f(x1,x2,x3)=(x1−x2+x3)2+(x2+x3)2+(x1+ax3)2, 其中 a 是参数
(I) 求 f(x1,x2,x3)=0 的解;
(II) 求 f(x1,x2,x3) 的规范形.
(20)
- (I) f(x1,x2,x3)=0 当且仅当⎩⎨⎧x1−x2+x3=0x2+x3=0x1+ax3=0对方程组的系数矩阵施以初等行变换得
- 101−11011a→10001021a−2.
- 当 a=2 时,方程组只有零解, 故 f(x1,x2,x3)=0 的解为 x=0;
- 当 a=2 时, 方程组有无穷多解, 通解为 x=k−2−11,k 为任意常数.
- 故 f(x1,x2,x3)=0 的解为 x=k−2−11,k 为任意常数.
- (II)
- 由 (I ) 知, 当 a=2 时, f(x1,x2,x3) 正定, f(x1,x2,x3) 的规范形为 y12+y22+y32.
- 当 a=2 时,求解 f 的规范形有以下两种解法.
- 解法 1f(x1,x2,x3)=2x12+2x22+6x32−2x1x2+6x1x3
- =2(x1−21x2+23x3)2+23(x2+x3)2,
- ⎩⎨⎧y1=2(x1−21x2+23x3),y2=26(x2+x3),y3=x3,
- 有 2−2223202626001=0, 所以 f(x1,x2,x3) 的规范形为 y12+y22.
- 解法 2f(x1,x2,x3)=2x12+2x22+6x32−2x1x2+6x1x3
- =(x1,x2,x3)2−13−120306x1x2x3=xTAx
- 由 ∣λE−A∣=0, 求 A 的特征值.
- ∣λE−A∣=λ−21−31λ−20−30λ−6
- =(λ−2)2(λ−6)−9(λ−2)−(λ−6)
- =λ3−10λ2+18λ=0,
- 解得 A 的特征值为 λ1=0,λ2=5+7,λ3=5−7.
- 所以 f(x1,x2,x3) 的规范形为 y12+y22.
(21)
(本题满分 11 分)
已知 a 是常数,且矩阵 A=112237a0−a 可经初等列变换化为矩阵 B=10−1a11211.
( I ) 求 a;
(II) 求满足 AP=B 的可逆矩阵 P.
(21)
- (I) 对矩阵 A,B 分别施以初等行变换, 得
- A=12a13027−a左下角三个0三阶矩阵103a01−a000,
- B=1a2011−111消出三个0100011002−a.
- 由题设知 r(A)=r(B), 故 a=2.
- (II) 由 (I) 知 a=2. 对矩阵 (A:B) 施以初等行变换, 得
(A:B)=11223720−210−1211211→1000106−203−104−104−10. - 记 B=(β1,β2,β3),
- 齐次的解A−621=0
- 非齐次的解A3−10=β1,A4−10=β2,A4−10=β3
- 故 AX=B 的解为X=3−6k1−1+2k1k14−6k2−1+2k2k24−6k3−1+2k3k3, 其中 k1,k2,k3 为任意常数.
- 由于 ∣X∣=k3−k2,
- 因此满足 AP=B 的可逆矩阵为
P=3−6k1−1+2k1k14−6k2−1+2k2k24−6k3−1+2k3k3, 其中 k1,k2,k3 为任意常数, 且 k2=k3.
(22)
(本题满分 11 分)
设随机变量 X 与 Y 相互独立, X 的概率分布为 P{X=1}=P{X=−1}=21,Y 服从参数为 λ 的泊松分布. 令 Z=XY.
( I ) 求 Cov(X,Z);
( II ) 求 Z 的概率分布.
(22)
解
这个问题涉及随机变量的协方差和概率分布。以下是对答案的详细解释:
(I) 求 Cov(X,Z)
- 计算协方差
- Cov(X,Z)=E(XZ)−E(X)⋅E(Z)Z=XYE(X⋅XY)−EX⋅E(XY)
- 独立E(X2)⋅E(Y)−E2(X)⋅E(Y)
- 计算 E(X) , E(X2),E(Y)
- E(X)=(−1)×21+1×21=0
- E(X2)=(−1)2×21+12×21=1
- E(Y)=λ(泊松分布的期望)
- 合并计算结果:Cov(X,Z)=1⋅λ−0⋅λ=λ
(II) 求 Z 的概率分布
- 三件套(常规思路):
- Fz(z)=p{z≤z}=P{XY⩽z}
- 对离散的全集分解可是泊松分布也是离散P{XY≤z,X=1}+P{XY⩽z,X=−1}
- 独立P{XY≤z}⋅P{X=1}+P{XY≤z}⋅P{X=−1}
- =21{Y⩽z}+21{−Y≤z}
- 往后做不动,有时间再写
- 本题是泊松分布:计算 P{Z=0}
- P{Z=0}=P{Y=0}=e−λ(泊松分布中 Y=0 的概率)
- 计算 P{Z=n} 对于 n=±1,±2,⋯
- P{Z=n}=P{XY=n}=P{X=∣n∣n,Y=∣n∣}
- =P{X=∣n∣n}⋅P{Y=∣n∣}(因为 X 和 Y 相互独立)
- =21⋅e−λ∣n∣!λ∣n∣(泊松分布中 Y=∣n∣ 的概率)
(23)
(本题满分 11 分)
设总体 X 的概率密度为f(x;σ)=2σ1e−σ∣x∣,−∞<x<+∞,其中 σ∈(0,+∞) 为未知参数, X1,X2,⋯,Xn 为来自总体 X 的简单随机样本. 记 σ 的最大似然估计量为 σ^.
(I) 求 σ^;
(II) 求 E(σ^),D(σ^).
(23)
【解】(1) 设 x1,x2,⋯,xn 为样本观测值, 这里的σ相当于之前的θ
- 写出似然函数为L(σ)=i=1∏nf(x1;σ)=(21)n⋅σn1⋅e−σ1∑i=1n∣xi∣,−∞<xi<+∞
- 取对数则 lnL(σ)=−nln2−nlnσ−σ1i=1∑n∣xi∣
- 求导找可能的极值点(驻点),得 dσdlnL(σ)=−σn+σ21i=1∑n∣xi∣=0,
- 解得 σ=n1i=1∑n∣xi∣, 所以 加帽子σ^=n1i=1∑n∣Xi∣
(II) 由于
- E(∣X∣)=∫−∞+∞∣x∣f(x;σ)dx=∫−∞+∞∣x∣2σ1e−σLxdx=σ1∫0+∞xe−σxdx=σ,因此
- Eσ^=n1i=1∑nE(∣Xi∣)=E(∣X∣)=σ又因为
- E(∣X∣2)=E(X2)=∫−∞+∞x2f(x;σ)dx=∫−∞+∞x22σ1e−σL∣dx=σ1∫0+∞x2e−σxdx=2σ2,
- D(∣X∣)=E(∣X∣2)−[E(∣X∣)]2=σ2,所以
- Dσ^=n21i=1∑nD(∣Xi∣)=nD(∣X∣)=nσ2.

