一、选择题 (本题共 8 小题, 每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有一项符合题目 要求,把所选项前的字母填在题后的括号内. )
(1) 已知极限 lim x → 0 x − arctan x x k = c \displaystyle \lim _{x \rightarrow 0} \frac{x-\arctan x}{x^{k}}=c x → 0 lim x k x − arctan x = c k , c k, c k , c c ≠ 0 c \neq 0 c = 0 ( ) (\quad) ( ) k = 2 , c = − 1 2 k=2, c=-\frac{1}{2} k = 2 , c = − 2 1 k = 2 , c = 1 2 k=2, c=\frac{1}{2} k = 2 , c = 2 1 k = 3 , c = − 1 3 k=3, c=-\frac{1}{3} k = 3 , c = − 3 1 k = 3 , c = 1 3 k=3, c=\frac{1}{3} k = 3 , c = 3 1
(1) 答 应选(D). 解: x → 0 x \rightarrow 0 x → 0 x − sin x ∼ 1 6 x 3 x-\sin x \sim \frac{1}{6} x^3 x − sin x ∼ 6 1 x 3 x − arcsin x − − 1 6 x 3 , x-\arcsin x--\frac{1}{6} x^3, x − arcsin x − − 6 1 x 3 , x − tan x − − 1 3 x 3 x-\tan x--\frac{1}{3} x^3 x − tan x − − 3 1 x 3 x − arctan x − 1 3 x 3 x-\arctan x-\frac{1}{3} x^3 x − arctan x − 3 1 x 3 x − ln ( 1 + x ) − 1 2 x 2 x-\ln (1+x)-\frac{1}{2} x^2 x − ln ( 1 + x ) − 2 1 x 2 e x − 1 − x − 1 2 x 2 e^x-1-x-\frac{1}{2} x^2 e x − 1 − x − 2 1 x 2 当 x → 0 x \rightarrow 0 x → 0 x − arctan x ∼ 1 3 x 3 x-\arctan x \sim \frac{1}{3} x^3 x − arctan x ∼ 3 1 x 3 比较同次幂的系数和指数,所以 k = 3 , c = 1 3 k=3, c=\frac{1}{3} k = 3 , c = 3 1 (2) 曲面 x 2 + cos ( x y ) + y z + x = 0 x^{2}+\cos (x y)+y z+x=0 x 2 + cos ( x y ) + yz + x = 0 ( 0 , 1 , − 1 ) (0,1,-1) ( 0 , 1 , − 1 ) ( ) (\quad) ( ) x − y + z = − 2 x-y+z=-2 x − y + z = − 2 x + y + z = 0 x+y+z=0 x + y + z = 0 x − 2 y + z = − 3 x-2 y+z=-3 x − 2 y + z = − 3 x − y − z = 0 x-y-z=0 x − y − z = 0
(2) 答 应选 (A). 由于曲面在一点的切平面与曲面在该点的法向量垂直, 内积为0,故曲面在点 P P P ( x − x 0 , y − y 0 , z − z 0 ) ⋅ ( ∂ F ∂ x , ∂ F ∂ y , ∂ F ∂ z ) ∣ ( x 0 , y 0 , z 0 ) = 0 \displaystyle \begin{aligned} & \left.\left(x-x_0, y-y_0, z-z_0\right) \cdot\left(\frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z}\right)\right|_{\left(x_0, y_0, z_0\right)}=0 \end{aligned} ( x − x 0 , y − y 0 , z − z 0 ) ⋅ ( ∂ x ∂ F , ∂ y ∂ F , ∂ z ∂ F ) ( x 0 , y 0 , z 0 ) = 0 即∂ F ∂ x ∣ ( x 0 , y 0 , z 0 ) ( x − x 0 ) + ∂ F ∂ y ∣ ( x 0 , y 0 , z 0 ) ( y − y 0 ) + ∂ F ∂ z ∣ ( x 0 , y 0 , z 0 ) ( z − z 0 ) = 0. \displaystyle \begin{aligned} \left. \frac{\partial F}{\partial x}\right|_{\left(x_0, y_0, z_0\right)}\left(x-x_0\right)+\left.\frac{\partial F}{\partial y}\right|_{\left(x_0, y_0, z_0\right)}\left(y-y_0\right)+\left.\frac{\partial F}{\partial z}\right|_{\left(x_0, y_0, z_0\right)}\left(z-z_0\right)=0 . \end{aligned} ∂ x ∂ F ( x 0 , y 0 , z 0 ) ( x − x 0 ) + ∂ y ∂ F ( x 0 , y 0 , z 0 ) ( y − y 0 ) + ∂ z ∂ F ( x 0 , y 0 , z 0 ) ( z − z 0 ) = 0. 由x 2 + cos ( x y ) + y z + x = 0 x^{2}+\cos (x y)+y z+x=0 x 2 + cos ( x y ) + yz + x = 0 F ( x , y , z ) = x 2 + cos ( x y ) + y z + x , \displaystyle \begin{aligned} F(x, y, z)=x^2+\cos (x y)+y z+x, \end{aligned} F ( x , y , z ) = x 2 + cos ( x y ) + yz + x , ( F x ′ , F y ′ , F z ′ ) ∣ ( 0 , 1 , − 1 ) = ( 1 , − 1 , 1 ) \displaystyle \begin{aligned} \left(F_x^{\prime}, F_y^{\prime}, F_z^{\prime}\right)|_{(0,1,-1)}=(1,-1,1) \end{aligned} ( F x ′ , F y ′ , F z ′ ) ∣ ( 0 , 1 , − 1 ) = ( 1 , − 1 , 1 ) F x ′ = 2 x − y sin ( x y ) + 1 ⇒ 1 \displaystyle \begin{aligned} F_x^{\prime}=2 x-y \sin (x y)+1 \quad \Rightarrow 1 \end{aligned} F x ′ = 2 x − y sin ( x y ) + 1 ⇒ 1 F y ′ = − x sin ( x y ) + z ⇒ − 1 \displaystyle \begin{aligned} F_y^{\prime}=-x \sin (x y)+z \quad \Rightarrow-1 \end{aligned} F y ′ = − x sin ( x y ) + z ⇒ − 1 F z ′ = y ⇒ 1 \displaystyle \begin{aligned} F_z^{\prime}=y \quad \Rightarrow 1 \end{aligned} F z ′ = y ⇒ 1 代入点法式方程:1 ⋅ ( x − 0 ) + ( − 1 ) ⋅ ( y − 1 ) + 1 ⋅ ( z + 1 ) = 0 \displaystyle \begin{aligned} 1 \cdot(x-0)+(-1) \cdot(y-1)+1 \cdot(z+1)=0 \end{aligned} 1 ⋅ ( x − 0 ) + ( − 1 ) ⋅ ( y − 1 ) + 1 ⋅ ( z + 1 ) = 0 所以曲面 F ( x , y , z ) = 0 F(x, y, z)=0 F ( x , y , z ) = 0 ( 0 , 1 , − 1 ) (0,1,-1) ( 0 , 1 , − 1 ) x − y + z + 2 = 0 \displaystyle \begin{aligned} x-y+z+2=0 \end{aligned} x − y + z + 2 = 0 (3) 设 f ( x ) = ∣ x − 1 2 ∣ , b n = 2 ∫ 0 1 f ( x ) sin n π x d x ( n = 1 , 2 , ⋯ ) \displaystyle f(x)=\left|x-\frac{1}{2}\right|, b_{n}=2 \int_{0}^{1} f(x) \sin n \pi x \mathrm{~d} x(n=1,2, \cdots) f ( x ) = x − 2 1 , b n = 2 ∫ 0 1 f ( x ) sin nπ x d x ( n = 1 , 2 , ⋯ ) S ( x ) = ∑ n = 1 ∞ b n sin n π x \displaystyle S(x)=\sum_{n=1}^{\infty} b_{n} \sin n \pi x S ( x ) = n = 1 ∑ ∞ b n sin nπ x S ( − 9 4 ) = S\left(-\frac{9}{4}\right)= S ( − 4 9 ) = 3 4 \frac{3}{4} 4 3 1 4 \frac{1}{4} 4 1 − 1 4 -\frac{1}{4} − 4 1 − 3 4 -\frac{3}{4} − 4 3
(3) 答 应选(C).S ( x ) S(x) S ( x ) f ( x ) f(x) f ( x ) S ( − 9 4 ) = S ( − 1 4 ) = − S ( 1 4 ) = − f ( 1 4 ) = − 1 4 . S\left(-\frac{9}{4}\right)=S\left(-\frac{1}{4}\right)=-S\left(\frac{1}{4}\right)=-f\left(\frac{1}{4}\right)=-\frac{1}{4} \text {. } S ( − 4 9 ) = S ( − 4 1 ) = − S ( 4 1 ) = − f ( 4 1 ) = − 4 1 . (4) 设 L 1 : x 2 + y 2 = 1 , L 2 : x 2 + y 2 = 2 , L 3 : x 2 + 2 y 2 = 2 , L 4 : 2 x 2 + y 2 = 2 L_{1}: x^{2}+y^{2}=1, L_{2}: x^{2}+y^{2}=2, L_{3}: x^{2}+2 y^{2}=2, L_{4}: 2 x^{2}+y^{2}=2 L 1 : x 2 + y 2 = 1 , L 2 : x 2 + y 2 = 2 , L 3 : x 2 + 2 y 2 = 2 , L 4 : 2 x 2 + y 2 = 2 I i = ∮ L i ( y + y 3 6 ) d x + ( 2 x − x 3 3 ) d y ( i = 1 , 2 , 3 , 4 ) I_{i}=\oint_{L_{i}}\left(y+\frac{y^{3}}{6}\right) \mathrm{d} x+\left(2 x-\frac{x^{3}}{3}\right) \mathrm{d} y(i=1,2,3,4) I i = ∮ L i ( y + 6 y 3 ) d x + ( 2 x − 3 x 3 ) d y ( i = 1 , 2 , 3 , 4 ) max { I 1 , I 2 , I 3 , I 4 } = ( ) \max \left\{I_{1}, I_{2}, I_{3}, I_{4}\right\}=(\quad) max { I 1 , I 2 , I 3 , I 4 } = ( ) I 1 I_{1} I 1 I 2 I_{2} I 2 I 3 I_{3} I 3 I 4 I_{4} I 4
(4) 答 应选(D). D 1 : x 2 + y 2 ⩽ 1 ; D 2 : x 2 + y 2 ⩽ 2 ; D 3 : x 2 2 + y 2 ⩽ 1 ; D 4 : x 2 + y 2 2 ⩽ 1 , D_1: x^2+y^2 \leqslant 1 ; D_2: x^2+y^2 \leqslant 2 ; D_3: \frac{x^2}{2}+y^2 \leqslant 1 ; D_4: x^2+\frac{y^2}{2} \leqslant 1 \text {, } D 1 : x 2 + y 2 ⩽ 1 ; D 2 : x 2 + y 2 ⩽ 2 ; D 3 : 2 x 2 + y 2 ⩽ 1 ; D 4 : x 2 + 2 y 2 ⩽ 1 , D = D 3 ∩ D 4 D=D_3 \cap D_4 D = D 3 ∩ D 4 I i = ∮ L 0 ( y + y 3 6 ) d x + ( 2 x − x 3 3 ) d y = ∬ D 0 [ ( 2 − x 2 ) − ( 1 + 1 2 y 2 ) ] d x d y \displaystyle \begin{aligned} I_i & =\oint_{L_0}\left(y+\frac{y^3}{6}\right) \mathrm{d} x+\left(2 x-\frac{x^3}{3}\right) \mathrm{d} y=\iint_{D_0}\left[\left(2-x^2\right)-\left(1+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y \end{aligned} I i = ∮ L 0 ( y + 6 y 3 ) d x + ( 2 x − 3 x 3 ) d y = ∬ D 0 [ ( 2 − x 2 ) − ( 1 + 2 1 y 2 ) ] d x d y = ∬ D 0 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y . \displaystyle \begin{aligned} =\iint_{D_0}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y . \end{aligned} = ∬ D 0 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y . I 1 = ∬ D 1 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y < ∬ D [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y \displaystyle \begin{aligned} I_1 & =\iint_{D_1}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y<\iint_D\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y \end{aligned} I 1 = ∬ D 1 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y < ∬ D [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y < ∬ D 4 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y = I 4 ; I 3 = ∬ D 4 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y = ∬ D [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y + \displaystyle \begin{aligned} <\iint_{D_4}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y=I_4 ; \\I_3 & =\iint_{D_4}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y=\iint_D\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y+ \end{aligned} < ∬ D 4 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y = I 4 ; I 3 = ∬ D 4 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y = ∬ D [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y + ∬ D 1 − D 0 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y < ∬ D [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y < I 4 ; I 2 = ∬ D i [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y = ∬ D 4 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y + ∬ D 3 − D 4 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y < ∭ D 4 [ 1 − ( x 2 + 1 2 y 2 ) ] d x d y = I 4 . \displaystyle \begin{array}{r}\iint_{D_1-D_0}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y<\iint_D\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y<I_4 ; \\I_2=\iint_{D_i}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y=\iint_{D_4}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y+ \\\iint_{D_3-D_4}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y<\iiint_{D_4}\left[1-\left(x^2+\frac{1}{2} y^2\right)\right] \mathrm{d} x \mathrm{~d} y=I_4 .\end{array} ∬ D 1 − D 0 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y < ∬ D [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y < I 4 ; I 2 = ∬ D i [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y = ∬ D 4 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y + ∬ D 3 − D 4 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y < ∭ D 4 [ 1 − ( x 2 + 2 1 y 2 ) ] d x d y = I 4 . max { I 1 , I 2 , I 3 , I 4 } = I 4 \max \left\{I_1, I_2, I_3, I_4\right\}=I_4 max { I 1 , I 2 , I 3 , I 4 } = I 4 (5) 设 A , B , C \boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C} A , B , C n n n A B = C \boldsymbol{A B}=\boldsymbol{C} AB = C B \boldsymbol{B} B C \boldsymbol{C} C A \boldsymbol{A} A C \boldsymbol{C} C A \boldsymbol{A} A C \boldsymbol{C} C B \boldsymbol{B} B C \boldsymbol{C} C B \boldsymbol{B} B
(5) 答 应选(B).A = ( α 1 , α 2 , ⋯ , α n ) , C = ( γ 1 , γ 2 , ⋯ , γ n ) \boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right), C=\left(\gamma_1, \gamma_2, \cdots, \gamma_n\right) A = ( α 1 , α 2 , ⋯ , α n ) , C = ( γ 1 , γ 2 , ⋯ , γ n ) α i , γ i ( i = 1 , 2 , ⋯ , n ) \boldsymbol{\alpha}_i, \gamma_i(i=1,2, \cdots, n) α i , γ i ( i = 1 , 2 , ⋯ , n ) n n n ( α 1 , α 2 , ⋯ , α n ) B = ( γ 1 , γ 2 , ⋯ , γ n ) , \displaystyle \begin{aligned} \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right) \boldsymbol{B}=\left(\boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \cdots, \boldsymbol{\gamma}_n\right), \end{aligned} ( α 1 , α 2 , ⋯ , α n ) B = ( γ 1 , γ 2 , ⋯ , γ n ) , ( α 1 , α 2 , ⋯ , α n ) = ( γ 1 , γ 2 , ⋯ , γ n ) B − 1 , \displaystyle \begin{aligned} \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right)=\left(\boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \cdots, \gamma_n\right) \boldsymbol{B}^{-1}, \end{aligned} ( α 1 , α 2 , ⋯ , α n ) = ( γ 1 , γ 2 , ⋯ , γ n ) B − 1 , A A A α 1 , α 2 , ⋯ , α n \alpha_1, \alpha_2, \cdots, \alpha_n α 1 , α 2 , ⋯ , α n C C C γ 1 , γ 2 , ⋯ , γ n \gamma_1, \gamma_2, \cdots, \gamma_n γ 1 , γ 2 , ⋯ , γ n A A A C C C B \boldsymbol{B} B A \boldsymbol{A} A n n n A \boldsymbol{A} A C \boldsymbol{C} C A \boldsymbol{A} A n n n C \boldsymbol{C} C n n n C \boldsymbol{C} C A B = ( 1 1 0 0 ) ( 1 1 1 0 ) = ( 2 1 0 0 ) = C , \displaystyle \boldsymbol{A B}=\left(\begin{array}{ll}1 & 1 \\0 & 0\end{array}\right)\left(\begin{array}{ll}1 & 1 \\1 & 0\end{array}\right)=\left(\begin{array}{ll}2 & 1 \\0 & 0\end{array}\right)=\boldsymbol{C}, AB = ( 1 0 1 0 ) ( 1 1 1 0 ) = ( 2 0 1 0 ) = C , A = ( 1 1 0 0 ) \displaystyle \boldsymbol{A}=\left(\begin{array}{ll}1 & 1 \\ 0 & 0\end{array}\right) A = ( 1 0 1 0 ) ( 1 , 1 ) , ( 0 , 0 ) (1,1),(0,0) ( 1 , 1 ) , ( 0 , 0 ) C = ( 2 1 0 0 ) \displaystyle \boldsymbol{C}=\left(\begin{array}{ll}2 & 1 \\ 0 & 0\end{array}\right) C = ( 2 0 1 0 ) ( 2 , 1 ) , ( 0 , 0 ) (2,1),(0,0) ( 2 , 1 ) , ( 0 , 0 ) A m × n B n × s = C m × s A_{m \times n} B_{n \times s}=C_{m \times s} A m × n B n × s = C m × s C C C A A A C C C B B B (6) 矩阵 ( 1 a 1 a b a 1 a 1 ) \displaystyle \left(\begin{array}{lll}1 & a & 1 \\ a & b & a \\ 1 & a & 1\end{array}\right) 1 a 1 a b a 1 a 1 ( 2 0 0 0 b 0 0 0 0 ) \displaystyle \left(\begin{array}{lll}2 & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 0\end{array}\right) 2 0 0 0 b 0 0 0 0 ( ) (\quad) ( ) a = 0 , b = 2 a=0, b=2 a = 0 , b = 2 a = 0 , b a=0, b a = 0 , b a = 2 , b = 0 a=2, b=0 a = 2 , b = 0 a = 2 , b a=2, b a = 2 , b
(6) 答 应选(B).B = B= B = ( 2 0 0 0 b 0 0 0 0 ) \displaystyle \left(\begin{array}{lll}2 & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 0\end{array}\right) 2 0 0 0 b 0 0 0 0 2 , b , 0 2, b, 0 2 , b , 0 A = ( 1 a 1 a b a 1 a 1 ) \displaystyle A=\left(\begin{array}{lll}1 & a & 1 \\ a & b & a \\ 1 & a & 1\end{array}\right) A = 1 a 1 a b a 1 a 1 a , b a, b a , b ∣ λ E − A ∣ = ∣ λ − 1 − a − 1 − a λ − b − a − 1 − a λ − 1 ∣ = λ [ ( λ − 2 ) ( λ − b ) − 2 a 2 ] , \displaystyle |\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{ccc}\lambda-1 & -a & -1 \\-a & \lambda-b & -a \\-1 & -a & \lambda-1\end{array}\right|=\lambda\left[(\lambda-2)(\lambda-b)-2 a^2\right], ∣ λ E − A ∣ = λ − 1 − a − 1 − a λ − b − a − 1 − a λ − 1 = λ [ ( λ − 2 ) ( λ − b ) − 2 a 2 ] , a = 0 a=0 a = 0 A \boldsymbol{A} A 2 , b , 0 2, b, 0 2 , b , 0 b b b a = 2 , b = 0 a=2, b=0 a = 2 , b = 0 A \boldsymbol{A} A 4 , − 2 , 0 4,-2,0 4 , − 2 , 0 A \boldsymbol{A} A B \boldsymbol{B} B (7) 设 X 1 , X 2 , X 3 X_{1}, X_{2}, X_{3} X 1 , X 2 , X 3 X 1 ∼ N ( 0 , 1 ) , X 2 ∼ N ( 0 , 2 2 ) , X 3 ∼ N ( 5 , 3 2 ) , p i = P { − 2 ⩽ X i ⩽ 2 } X_{1} \sim N(0,1), X_{2} \sim N\left(0,2^{2}\right), X_{3} \sim N\left(5,3^{2}\right), p_{i}=P\left\{-2 \leqslant X_{i} \leqslant 2\right\} X 1 ∼ N ( 0 , 1 ) , X 2 ∼ N ( 0 , 2 2 ) , X 3 ∼ N ( 5 , 3 2 ) , p i = P { − 2 ⩽ X i ⩽ 2 } ( i = 1 , 2 , 3 ) (i=1,2,3) ( i = 1 , 2 , 3 ) ( ) (\quad) ( ) p 1 > p 2 > p 3 p_{1}>p_{2}>p_{3} p 1 > p 2 > p 3 p 2 > p 1 > p 3 p_{2}>p_{1}>p_{3} p 2 > p 1 > p 3 p 3 > p 1 > p 2 p_{3}>p_{1}>p_{2} p 3 > p 1 > p 2 p 1 > p 3 > p 2 p_{1}>p_{3}>p_{2} p 1 > p 3 > p 2
(7) 解![[24Kira概率醒脑讲义#例5 4 3-29 20]] (未创建)
一定要有这种将正态分布转化为标准正态分布的思路
计算每个 p i p_i p i
对于 X 1 ∼ N ( 0 , 1 ) X_1 \sim N(0,1) X 1 ∼ N ( 0 , 1 ) 使用标准正态分布图 P 1 = Φ ( 2 ) − Φ ( − 2 ) P_1 = \Phi(2) - \Phi(-2) P 1 = Φ ( 2 ) − Φ ( − 2 ) 对于 X 2 ∼ N ( 0 , 2 2 ) X_2 \sim N\left(0,2^{2}\right) X 2 ∼ N ( 0 , 2 2 ) x 2 − 0 2 = x 2 2 ∽ N ( 0 , 1 ) \frac{x_2-0}{2}=\frac{x_2}{2} \backsim N(0\text{,}1) 2 x 2 − 0 = 2 x 2 ∽ N ( 0 , 1 ) p 2 = P { − 2 ⩽ X 2 ⩽ 2 } = x 2 − μ σ = x 2 − 0 2 P ∣ − 1 ⩽ X 2 2 ⩽ 1 } = Φ ( 1 ) − Φ ( − 1 ) = \displaystyle \begin {aligned}\left.p_2=P\left\{-2 \leqslant X_2 \leqslant 2\right\}\xlongequal[]{\frac{x_2-\mu}{\sigma}=\frac{x_2-0}{2}}P \mid-1 \leqslant \frac{X_2}{2} \leqslant 1\right\}=\Phi(1)-\Phi(-1)= \end{aligned} p 2 = P { − 2 ⩽ X 2 ⩽ 2 } σ x 2 − μ = 2 x 2 − 0 P ∣ − 1 ⩽ 2 X 2 ⩽ 1 } = Φ ( 1 ) − Φ ( − 1 ) = 对于 X 3 ∼ N ( 5 , 3 2 ) X_3 \sim N\left(5,3^{2}\right) X 3 ∼ N ( 5 , 3 2 ) x 3 − 5 3 ∽ N ( 0 , 1 ) \frac{x_3-5}{3} \backsim N(0,1) 3 x 3 − 5 ∽ N ( 0 , 1 ) p 3 = P { − 2 ⩽ X 3 ⩽ 2 } = x 3 − μ σ P { − 7 3 ⩽ X 3 − 5 3 ⩽ − 1 } = Φ ( − 1 ) − Φ ( − 7 3 ) \displaystyle \begin {aligned}p_3=P\left\{-2 \leqslant X_3 \leqslant 2\right\}\xlongequal[]{\frac{x_3-\mu}{\sigma}}P\left\{-\frac{7}{3} \leqslant \frac{X_3-5}{3} \leqslant-1\right\}=\Phi(-1)-\Phi\left(-\frac{7}{3}\right) \end{aligned} p 3 = P { − 2 ⩽ X 3 ⩽ 2 } σ x 3 − μ P { − 3 7 ⩽ 3 X 3 − 5 ⩽ − 1 } = Φ ( − 1 ) − Φ ( − 3 7 ) 画图比较 p 1 , p 2 , p 3 p_1, p_2, p_3 p 1 , p 2 , p 3
2 ⩽ P 1 < 2 − 1 < P 2 < 1 − 7 3 < P 3 < − 1 → 比较宽度 \displaystyle \begin{array}{l}2 \leqslant P_1<2 \\ -1<P_2<1 \\ -\frac{7}{3}<P_3<-1\end{array}\xrightarrow[]{\text{比较宽度}} 2 ⩽ P 1 < 2 − 1 < P 2 < 1 − 3 7 < P 3 < − 1 比较宽度 P 1 > P 2 > P 3 P_1>P_2>P_3 P 1 > P 2 > P 3 结论
综上所述,p 1 > p 2 > p 3 p_1 > p_2 > p_3 p 1 > p 2 > p 3 因此,正确答案为 (A) p 1 > p 2 > p 3 p_1 > p_2 > p_3 p 1 > p 2 > p 3 这个解释不仅展示了每个概率的计算过程,还比较了它们之间的大小关系,最终得出正确的结论。
答 应选 (A).
p 1 = Φ ( 2 ) − Φ ( − 2 ) = 2 Φ ( 2 ) − 1 p_1=\Phi(2)-\Phi(-2)=2 \Phi(2)-1 p 1 = Φ ( 2 ) − Φ ( − 2 ) = 2Φ ( 2 ) − 1 p 2 = Φ ( 2 2 ) − Φ ( − 2 2 ) = 2 Φ ( 1 ) − 1 , \displaystyle \begin{aligned} p_2=\Phi\left(\frac{2}{2}\right)-\Phi\left(\frac{-2}{2}\right)=2 \Phi(1)-1, \end{aligned} p 2 = Φ ( 2 2 ) − Φ ( 2 − 2 ) = 2Φ ( 1 ) − 1 , p 3 = Φ ( 2 − 5 3 ) − Φ ( − 2 − 5 3 ) = Φ ( − 1 ) − Φ ( − 7 3 ) , \displaystyle \begin{aligned} p_3=\Phi\left(\frac{2-5}{3}\right)-\Phi\left(\frac{-2-5}{3}\right)=\Phi(-1)-\Phi\left(-\frac{7}{3}\right), \end{aligned} p 3 = Φ ( 3 2 − 5 ) − Φ ( 3 − 2 − 5 ) = Φ ( − 1 ) − Φ ( − 3 7 ) , p 1 > p 2 p_1>p_2 p 1 > p 2 p 2 > 0.5 , p 3 < 0.5 p_2>0.5, p_3<0.5 p 2 > 0.5 , p 3 < 0.5 p 2 > p 3 p_2>p_3 p 2 > p 3 p 1 > p 2 > p 3 p_1>p_2>p_3 p 1 > p 2 > p 3 p i = P { − 2 ⩽ X i ⩽ 2 } p_i=P\left\{-2 \leqslant X_i \leqslant 2\right\} p i = P { − 2 ⩽ X i ⩽ 2 } p 1 > p 2 > p 3 p_1>p_2>p_3 p 1 > p 2 > p 3 (8) 设随机变量 X ∼ t ( n ) , Y ∼ F ( 1 , n ) X \sim t(n), Y \sim F(1, n) X ∼ t ( n ) , Y ∼ F ( 1 , n ) α ( 0 < α < 0.5 ) \alpha(0<\alpha<0.5) α ( 0 < α < 0.5 ) c c c P { X > c } = α P\{X>c\}=\alpha P { X > c } = α P { Y > c 2 } = ( ) P\left\{Y>c^{2}\right\}=(\quad) P { Y > c 2 } = ( ) α \alpha α 1 − α 1-\alpha 1 − α 2 α 2 \alpha 2 α 1 − 2 α 1-2 \alpha 1 − 2 α
(8) 答 应选(C).解 由 X ∼ t ( n ) X \sim t(n) X ∼ t ( n ) X 2 ∼ F ( 1 , n ) X^2 \sim F(1, n) X 2 ∼ F ( 1 , n ) P { Y > c 2 } = P { X 2 > c 2 } = P { X > c } + P { X < − c } = 2 α , P\left\{Y>c^2\right\}=P\left\{X^2>c^2\right\}=P\{X>c\}+P\{X<-c\}=2 \alpha, P { Y > c 2 } = P { X 2 > c 2 } = P { X > c } + P { X < − c } = 2 α , 二、填空题 本题共 6 小题,每小题 4 分, 共 24 分, 把答案填在题中横线上
(9) 设函数 y = f ( x ) y=f(x) y = f ( x ) y − x = e x ( 1 − y ) y-x=\mathrm{e}^{x(1-y)} y − x = e x ( 1 − y ) lim n → ∞ n [ f ( 1 n ) − 1 ] = \displaystyle \lim _{n \rightarrow \infty} n\left[f\left(\frac{1}{n}\right)-1\right]= n → ∞ lim n [ f ( n 1 ) − 1 ] =
(9) 这样的格式应该更加清晰和组织化。
(10) 已知 y 1 = e 3 x − x e 2 x , y 2 = e x − x e 2 x , y 3 = − x e 2 x y_{1}=\mathrm{e}^{3 x}-x \mathrm{e}^{2 x}, y_{2}=\mathrm{e}^{x}-x \mathrm{e}^{2 x}, y_{3}=-x \mathrm{e}^{2 x} y 1 = e 3 x − x e 2 x , y 2 = e x − x e 2 x , y 3 = − x e 2 x y = y= y =
(10) 分析 本题主要考查二阶常系数非齐次线性微分方程通解的结构。 其通解等于对应的齐次线性微分方程的两个线性无关的解的线性组合加上一个特解。 设 y 1 ( x ) , y 2 ( x ) y_1(x), y_2(x) y 1 ( x ) , y 2 ( x ) y ′ ′ + P ( x ) y ′ + Q ( x ) y = f ( x ) y^{\prime \prime}+P(x) y^{\prime}+Q(x) y=f(x) y ′′ + P ( x ) y ′ + Q ( x ) y = f ( x ) y 1 ( x ) − y 2 ( x ) y_1(x)-y_2(x) y 1 ( x ) − y 2 ( x ) 对应的齐次线性方程的解 . 答 应填 C 1 e x + C 2 e 3 x − x e 2 x C_1 \mathrm{e}^x+C_2 \mathrm{e}^{3 x}-x \mathrm{e}^{2 x} C 1 e x + C 2 e 3 x − x e 2 x C 1 , C 2 C_1, C_2 C 1 , C 2 该非齐次线性微分方程对应的齐次线性微分方程的两个线性无关的解 y 1 − y 3 = e 3 x y_1-y_3=\mathrm{e}^{3 x} y 1 − y 3 = e 3 x y 2 − y 3 = e x \displaystyle \begin{aligned}y_2-y_3=\mathrm{e}^x\end{aligned} y 2 − y 3 = e x 则齐次通解为y = C 1 e 3 x + C 2 e x y=C_1 e^{3 x}+C_2 e^x y = C 1 e 3 x + C 2 e x 非齐次特解为y 3 = − x e 2 x y_3=-x \mathrm{e}^{2 x} y 3 = − x e 2 x 所以该方程的通解为:齐次方程通解+非齐次方程特解y = C 1 e x + C 2 e 3 x − x e 2 x y=C_1 \mathrm{e}^x+C_2 \mathrm{e}^{3 x}-x \mathrm{e}^{2 x} y = C 1 e x + C 2 e 3 x − x e 2 x C 1 , C 2 C_1, C_2 C 1 , C 2 (11) 设 { x = sin t , y = t sin t + cos t \displaystyle \left\{\begin{array}{l}x=\sin t, \\ y=t \sin t+\cos t\end{array}\right. { x = sin t , y = t sin t + cos t t t t d 2 y d x 2 ∣ t = π 4 = \left.\frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}\right|_{t=\frac{\pi}{4}}= d x 2 d 2 y t = 4 π =
(11) 已知 x = sin t x = \sin t x = sin t y = t sin t + cos t y = t \sin t + \cos t y = t sin t + cos t 计算 d y d x = d y d t d x d t \displaystyle \begin{aligned}\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\end{aligned} d x d y = d t d x d t d y 计算 d x d t \frac{dx}{dt} d t d x d y d t \frac{dy}{dt} d t d y d x d t = cos t \frac{dx}{dt} = \cos t d t d x = cos t d y d t = sin t + t cos t − sin t \frac{dy}{dt} = \sin t + t \cos t - \sin t d t d y = sin t + t cos t − sin t 应用链式法则 d y d x = d y d t d x d t = sin t + t cos t − sin t cos t = t \displaystyle \begin{aligned}\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{\sin t + t \cos t - \sin t}{\cos t}=t\end{aligned} d x d y = d t d x d t d y = cos t sin t + t cos t − sin t = t 已知 d y d x = t \frac{dy}{dx} = t d x d y = t d 2 y d x 2 = d d t ( d y d x ) ⋅ d t d x \displaystyle \begin{aligned}\frac{d^2 y}{dx^2}=\frac{d}{dt}(\frac{dy}{dx}) \cdot \frac{dt}{dx}\end{aligned} d x 2 d 2 y = d t d ( d x d y ) ⋅ d x d t 计算 d d t ( d y d x ) \frac{d}{dt}(\frac{dy}{dx}) d t d ( d x d y ) d t d x \frac{dt}{dx} d x d t d d t ( d y d x ) = 1 \frac{d}{dt}(\frac{dy}{dx}) = 1 d t d ( d x d y ) = 1 d t d x = 1 d x d t = 1 cos t \displaystyle \begin{aligned}\frac{dt}{dx} = \frac{1}{\frac{dx}{dt}}=\frac{1}{\cos t}\end{aligned} d x d t = d t d x 1 = cos t 1 应用链式法则 d 2 y d x 2 = d d t ( d y d x ) ⋅ d t d x = 1 ⋅ 1 cos t = 1 cos t \displaystyle \begin{aligned}\frac{d^2 y}{dx^2} = \frac{d}{dt}(\frac{dy}{dx}) \cdot \frac{dt}{dx}=1 \cdot \frac{1}{\cos t}=\frac{1}{\cos t}\end{aligned} d x 2 d 2 y = d t d ( d x d y ) ⋅ d x d t = 1 ⋅ cos t 1 = cos t 1 在 t = π 4 t = \frac{\pi}{4} t = 4 π d 2 y d x 2 \frac{d^2 y}{dx^2} d x 2 d 2 y 代入 → t = π 4 d 2 y d x 2 = 1 cos π 4 = 2 \xrightarrow[]{t = \frac{\pi}{4}}\frac{d^2 y}{dx^2} = \frac{1}{\cos \frac{\pi}{4}}=\sqrt{2} t = 4 π d x 2 d 2 y = c o s 4 π 1 = 2 (12) ∫ 1 + ∞ ln x ( 1 + x ) 2 d x = \displaystyle \int_{1}^{+\infty} \frac{\ln x}{(1+x)^{2}} \mathrm{~d} x= ∫ 1 + ∞ ( 1 + x ) 2 ln x d x =
(12) 将积分重写为 − ∫ 1 + ∞ ln x d ( 1 1 + x ) = 分布 − [ ln x 1 + x ∣ 1 + ∞ − ∫ 1 + ∞ 1 x ( 1 + x ) d x ] \displaystyle -\int_1^{+\infty} \ln x \mathrm{d}\left(\frac{1}{1+x}\right)\xlongequal[]{\text{分布}}-\left[\left.\frac{\ln x}{1+x}\right|_1 ^{+\infty}-\int_1^{+\infty} \frac{1}{x(1+x)} \mathrm{d} x\right] − ∫ 1 + ∞ ln x d ( 1 + x 1 ) 分布 − [ 1 + x ln x 1 + ∞ − ∫ 1 + ∞ x ( 1 + x ) 1 d x ] 计算第一部分: − ln x 1 + x ∣ 1 + ∞ = 0 − 0 = 0 -\left.\frac{\ln x}{1+x}\right|_1^{+\infty}=0-0=0 − 1 + x l n x 1 + ∞ = 0 − 0 = 0 计算第二部分: ∫ 1 + ∞ d x x ( 1 + x ) = 拆开 ∫ 1 + ∞ ( 1 x − 1 x + 1 ) d x ⏟ = [ ln x − ln ( 1 + x ) ] ∣ 1 + ∞ = ln x 1 + x ∣ 1 + ∞ = ln 1 − ln 1 2 = ln 2 \displaystyle \int_1^{+\infty} \frac{\mathrm{d} x}{x(1+x)}\xlongequal[]{\text{拆开}}\underbrace{\int_1^{+\infty}\left(\frac{1}{x}-\frac{1}{x+1}\right) \mathrm{d} x}_{=\left.[\ln x-\ln (1+x)]\right|_1 ^{+\infty}}=\left.\ln \frac{x}{1+x}\right|_1^{+\infty}=\ln 1-\ln \frac{1}{2}=\ln 2 ∫ 1 + ∞ x ( 1 + x ) d x 拆开 = [ l n x − l n ( 1 + x )] ∣ 1 + ∞ ∫ 1 + ∞ ( x 1 − x + 1 1 ) d x = ln 1 + x x 1 + ∞ = ln 1 − ln 2 1 = ln 2 合并:= − [ 0 − ( ln 2 ) ] = ln 2 =-[0-(\ln 2)]=\ln 2 = − [ 0 − ( ln 2 )] = ln 2 (13) 设 A = ( a i j ) \boldsymbol{A}=\left(a_{i j}\right) A = ( a ij ) ∣ A ∣ |\boldsymbol{A}| ∣ A ∣ A \boldsymbol{A} A A i j A_{i j} A ij a i j a_{i j} a ij a i j + A i j = 0 a_{i j}+A_{i j}=0 a ij + A ij = 0 ( i , j = 1 , 2 , 3 ) (i, j=1,2,3) ( i , j = 1 , 2 , 3 ) ∣ A ∣ = |\boldsymbol{A}|= ∣ A ∣ =
(13) 答 应填 -1 .解 由 a i j + A i j = 0 ( i , j = 1 , 2 , 3 ) a_{i j}+A_{i j}=0(i, j=1,2,3) a ij + A ij = 0 ( i , j = 1 , 2 , 3 ) A \boldsymbol{A} A A ⋅ \boldsymbol{A}^{\cdot} A ⋅ A ∗ = − A T \boldsymbol{A}^*=-\boldsymbol{A}^{\mathrm{T}} A ∗ = − A T ∣ A ∗ ∣ = ( − 1 ) 3 ∣ A T ∣ = − ∣ A ∣ \left|\boldsymbol{A}^*\right|=(-1)^3\left|\boldsymbol{A}^{\mathrm{T}}\right|=-|\boldsymbol{A}| ∣ A ∗ ∣ = ( − 1 ) 3 A T = − ∣ A ∣ ∣ A ∗ ∣ = ∣ A ∣ 3 − 1 = ∣ A ∣ 2 \left|\boldsymbol{A}^*\right|=|\boldsymbol{A}|^{3-1}=|\boldsymbol{A}|^2 ∣ A ∗ ∣ = ∣ A ∣ 3 − 1 = ∣ A ∣ 2 ∣ A ∣ 2 + ∣ A ∣ = 0 |\boldsymbol{A}|^2+|\boldsymbol{A}|=0 ∣ A ∣ 2 + ∣ A ∣ = 0 ∣ A ∣ = − 1 |\boldsymbol{A}|=-1 ∣ A ∣ = − 1 ∣ A ∣ = 0 |\boldsymbol{A}|=0 ∣ A ∣ = 0 a 11 ≠ 0 a_{11} \neq 0 a 11 = 0 ∣ A ∣ = a 11 A 11 + a 12 A 12 + a 13 A 13 = − ( a 11 2 + a 12 2 + a 13 2 ) < 0 , |\boldsymbol{A}|=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}=-\left(a_{11}^2+a_{12}^2+a_{13}^2\right)<0, ∣ A ∣ = a 11 A 11 + a 12 A 12 + a 13 A 13 = − ( a 11 2 + a 12 2 + a 13 2 ) < 0 , ∣ A ∣ = 0 |A|=0 ∣ A ∣ = 0 ∣ A ∣ = − 1 |A|=-1 ∣ A ∣ = − 1 (14) 设随机变量 Y Y Y a a a P { Y ⩽ a + 1 ∣ Y > a } = P\{Y \leqslant a+1 \mid Y>a\}= P { Y ⩽ a + 1 ∣ Y > a } =
(14) ![[24Kira概率醒脑讲义#例5 2无记忆性]](未创建)解法 1: 写出指数分布的概率密度f ( x ) = { e − x : x > 0 0 else \displaystyle f(x)=\left\{\begin{array}{cc}e^{-x}: & x>0 \\ 0 & \text { else }\end{array}\right. f ( x ) = { e − x : 0 x > 0 else 使用条件概率和积分来计算:计算 P { Y ⩽ a + 1 ∣ Y > a } P\{Y \leqslant a+1 \mid Y>a\} P { Y ⩽ a + 1 ∣ Y > a } P { Y ⩽ a + 1 ∣ Y > a } = 条件概率 P { a < Y ⩽ a + 1 } P { Y > a } P\{Y \leqslant a+1 \mid Y>a\} \xlongequal[]{\text{条件概率}} \frac{P\{a<Y \leqslant a+1\}}{P\{Y>a\}} P { Y ⩽ a + 1 ∣ Y > a } 条件概率 P { Y > a } P { a < Y ⩽ a + 1 } 何处算概率,何处算积分 计算分子 P { a < Y ⩽ a + 1 } = 何处积分 ∫ a a + 1 e − x d x \displaystyle P\{a<Y \leqslant a+1\} \xlongequal[]{\text{何处积分}} \int_a^{a+1} \mathrm{e}^{-x} \mathrm{~d} x P { a < Y ⩽ a + 1 } 何处积分 ∫ a a + 1 e − x d x 计算分母 P { Y > a } = 何处积分 ∫ a + ∞ e − x d x \displaystyle P\{Y>a\} \xlongequal[]{\text{何处积分}} \int_a^{+\infty} \mathrm{e}^{-x} \mathrm{~d} x P { Y > a } 何处积分 ∫ a + ∞ e − x d x 合并计算 ∫ a a + 1 e − x d x ∫ a + ∞ e − x d x = ∫ e − x d x = − e − x e − a − e − a − 1 e − a = 1 − 1 e . \displaystyle \frac{\int_a^{a+1} \mathrm{e}^{-x} \mathrm{~d} x}{\int_a^{+\infty} \mathrm{e}^{-x} \mathrm{~d} x} \xlongequal[]{\int e^{-x} d x=-e^{-x}}\frac{\mathrm{e}^{-a}-\mathrm{e}^{-a-1}}{\mathrm{e}^{-a}}=1-\frac{1}{\mathrm{e}} . ∫ a + ∞ e − x d x ∫ a a + 1 e − x d x ∫ e − x d x = − e − x e − a e − a − e − a − 1 = 1 − e 1 . 解法 2:使用指数分布的无记忆性质 要掌握各种分布的写法 应用无记忆性 ( P { X > s + t ∣ X > s } = P { X > t } , t , s > 0 ) (P\{X>s+t \mid X>s\}=P\{X>t\}, t, s>0) ( P { X > s + t ∣ X > s } = P { X > t } , t , s > 0 ) 指数分布具有独特的“无记忆性”,意味着过去的信息(在这个例子中是 (Y>a)不影响未来的概率分布。 计算 P { Y ⩽ a + 1 ∣ Y > a } = 减法公式 1 − P { Y > a + 1 ∣ Y > a } = 1 − P { Y > 1 } = 1 − ∫ 1 + ∞ e − x d x = 1 − 1 e \displaystyle P\{Y \leqslant a+1| Y>a\}\xlongequal[]{\text{减法公式}}1-P\{Y>a+1|Y>a\}=1-P\{Y>1 \}=1-\int_1^{+\infty} \mathrm{e}^{-x} \mathrm{~d} x=1-\frac{1}{\mathrm{e}} P { Y ⩽ a + 1∣ Y > a } 减法公式 1 − P { Y > a + 1∣ Y > a } = 1 − P { Y > 1 } = 1 − ∫ 1 + ∞ e − x d x = 1 − e 1 这样的结构确保了逻辑关系的清晰性,并且每个计算步骤都得到了充分的解释。
这个问题是关于计算条件概率 P { Y ⩽ a + 1 ∣ Y > a } P\{Y \leqslant a+1 \mid Y>a\} P { Y ⩽ a + 1 ∣ Y > a } Y Y Y
P { Y ⩽ a + 1 ∣ Y > a } P\{Y \leqslant a+1 \mid Y>a\} P { Y ⩽ a + 1 ∣ Y > a } = 条件概率定义 P { a < Y ⩽ a + 1 } P { Y > a } \xlongequal[]{\text{条件概率定义}} \frac{P\{a<Y \leqslant a+1\}}{P\{Y>a\}} 条件概率定义 P { Y > a } P { a < Y ⩽ a + 1 } → 计算分子 P { a < Y ⩽ a + 1 } = ∫ a a + 1 e − x d x \displaystyle \xrightarrow[]{\text{计算分子}} P\{a<Y \leqslant a+1\} = \int_a^{a+1} e^{-x} \, \mathrm{d} x 计算分子 P { a < Y ⩽ a + 1 } = ∫ a a + 1 e − x d x Y Y Y 指数分布的概率密度函数为 e − x e^{-x} e − x → 计算分母 P { Y > a } = ∫ a + ∞ e − x d x \displaystyle \xrightarrow[]{\text{计算分母}} P\{Y>a\} = \int_a^{+\infty} e^{-x} \, \mathrm{d} x 计算分母 P { Y > a } = ∫ a + ∞ e − x d x = 计算积分 ∫ a a + 1 e − x d x ∫ a + ∞ e − x d x = 1 − 1 e \displaystyle \xlongequal[]{\text{计算积分}} \frac{\int_a^{a+1} e^{-x} \, \mathrm{d} x}{\int_a^{+\infty} e^{-x} \, \mathrm{d} x} = 1 - \frac{1}{e} 计算积分 ∫ a + ∞ e − x d x ∫ a a + 1 e − x d x = 1 − e 1 P { Y ⩽ a + 1 ∣ Y > a } = 1 − 1 e P\{Y \leqslant a+1 \mid Y>a\} = 1 - \frac{1}{e} P { Y ⩽ a + 1 ∣ Y > a } = 1 − e 1 此外,解法 2 基于指数分布的无记忆性质提供了另一个视角:
P { Y ⩽ a + 1 ∣ Y > a } P\{Y \leqslant a+1 \mid Y>a\} P { Y ⩽ a + 1 ∣ Y > a } = 指数分布的无记忆性 P { Y ⩽ 1 } \xlongequal[]{\text{指数分布的无记忆性}} P\{Y \leqslant 1\} 指数分布的无记忆性 P { Y ⩽ 1 } = 直接计算 1 − 1 e \xlongequal[]{\text{直接计算}} 1 - \frac{1}{e} 直接计算 1 − e 1 两种解法都得到了相同的结果 1 − 1 e 1 - \frac{1}{e} 1 − e 1
答 应填 1 − 1 e 1-\frac{1}{\mathrm{e}} 1 − e 1 P { Y ⩽ a + 1 ∣ Y > a } = P { a < Y ⩽ a + 1 } P { Y > a } = ∫ a a + 1 e − x d x ∫ a + ∞ e − x d x = 1 − 1 e . \displaystyle P\{Y \leqslant a+1 \mid Y>a\}=\frac{P\{a<Y \leqslant a+1\}}{P\{Y>a\}}=\frac{\int_a^{a+1} \mathrm{e}^{-x} \mathrm{~d} x}{\int_a^{+\infty} \mathrm{e}^{-x} \mathrm{~d} x}=1-\frac{1}{\mathrm{e}} . P { Y ⩽ a + 1 ∣ Y > a } = P { Y > a } P { a < Y ⩽ a + 1 } = ∫ a + ∞ e − x d x ∫ a a + 1 e − x d x = 1 − e 1 . P { Y ⩽ a + 1 ∣ Y > a } = P { Y ⩽ 1 } = 1 − 1 e P\{Y \leqslant a+1 \mid Y>a\}=P\{Y \leqslant 1\}=1-\frac{1}{\mathrm{e}} P { Y ⩽ a + 1 ∣ Y > a } = P { Y ⩽ 1 } = 1 − e 1
(15) (本题满分 10 分)计算 ∫ 0 1 f ( x ) x d x \displaystyle \int_{0}^{1} \frac{f(x)}{\sqrt{x}} \mathrm{~d} x ∫ 0 1 x f ( x ) d x f ( x ) = ∫ 1 x ln ( t + 1 ) t d t \displaystyle f(x)=\int_{1}^{x} \frac{\ln (t+1)}{t} \mathrm{~d} t f ( x ) = ∫ 1 x t ln ( t + 1 ) d t
(15) 计算定积分 ∫ 0 1 f ( x ) x d x \displaystyle \int_{0}^{1} \frac{f(x)}{\sqrt{x}} \, dx ∫ 0 1 x f ( x ) d x f ( x ) = ∫ 1 x ln ( t + 1 ) t d t \displaystyle f(x) = \int_{1}^{x} \frac{\ln(t + 1)}{t} \, dt f ( x ) = ∫ 1 x t ln ( t + 1 ) d t ∫ 0 1 f ( x ) x d x = 2 ∫ 0 1 f ( x ) d ( x ) \displaystyle \begin{aligned}\int_0^1 \frac{f(x)}{\sqrt{x}} d x=2 \int_0^1 f(x) d(\sqrt{x})\end{aligned} ∫ 0 1 x f ( x ) d x = 2 ∫ 0 1 f ( x ) d ( x ) = 分布 2 [ x ⋅ f ( x ) ∣ 0 1 ⏟ 0 − 0 = 0 − ∫ 0 1 x d [ f ( x ) ] ⏟ ∫ 0 1 x ⋅ ln ( x + 1 ) x d x ] \displaystyle \xlongequal[]{\text{分布}}2\left[\underbrace{\left.\sqrt{x} \cdot f(x)\right|_0 ^1}_{0-0=0}-\underbrace{\int_0^1 \sqrt{x} d\left[f(x)\right]}_{\int_0^1 \sqrt{x} \cdot \frac{\ln (x+1)}{x} d x}\right] 分布 2 0 − 0 = 0 x ⋅ f ( x ) 0 1 − ∫ 0 1 x ⋅ x l n ( x + 1 ) d x ∫ 0 1 x d [ f ( x ) ] = 整理 − 2 [ ∫ 0 1 ln ( x + 1 ) x d x ] \displaystyle \begin{aligned}\xlongequal[]{\text{整理}}-2\left[\int_0^1 \frac{\ln (x+1)}{\sqrt{x}} d x\right]\end{aligned} 整理 − 2 [ ∫ 0 1 x ln ( x + 1 ) d x ] 凑微分 d ( x ) d(\sqrt{x}) d ( x ) − 4 ∫ 0 1 ln ( x + 1 ) d ( x ) \displaystyle -4 \int_{0}^{1} \ln(x + 1) d(\sqrt{x}) − 4 ∫ 0 1 ln ( x + 1 ) d ( x ) 分部积分:= − 4 [ x ln ( x + 1 ) ∣ 0 1 − ∫ 0 1 x x + 1 d x ] \displaystyle =-4\left[\left.\sqrt{x} \ln (x+1)\right|_0 ^1-\int_0^1 \frac{\sqrt{x}}{x+1} \mathrm{~d} x\right] = − 4 [ x ln ( x + 1 ) 0 1 − ∫ 0 1 x + 1 x d x ] 第一部分:x ln ( x + 1 ) ∣ 0 1 = ln 2 \left.\sqrt{x} \ln (x+1)\right|_0 ^1=\ln 2 x ln ( x + 1 ) ∣ 0 1 = ln 2 计算第二部分:∫ 0 1 x x + 1 d x = x = t 2 , d x = 2 t d t x = t ∫ 0 1 t 1 + t 2 ⋅ 2 t d t = 2 ∫ 0 1 t 2 1 + t 2 d t \displaystyle \int_0^1 \frac{\sqrt{x}}{x+1} \mathrm{~d} x\xlongequal[x=t^2, d x=2 t d t]{\sqrt{x}=t}\int_0^1 \frac{t}{1+t^2} \cdot 2 t d t=2 \int_0^1 \frac{t^2}{1+t^2} d t ∫ 0 1 x + 1 x d x x = t x = t 2 , d x = 2 t d t ∫ 0 1 1 + t 2 t ⋅ 2 t d t = 2 ∫ 0 1 1 + t 2 t 2 d t 拆开分子:∫ 0 1 t 2 1 + t 2 d t = t 2 = t 2 + 1 − 1 ∫ 0 1 t 2 + 1 − 1 1 + t 2 d t = ∫ 0 1 1 d t − ∫ 0 1 1 1 + t 2 d t ] = 1 − arctan t ∣ 0 1 = arctan 0 = 0 arctan 1 = π 4 1 − π 4 \displaystyle \int_0^1 \frac{t^2}{1+t^2} d t\xlongequal[]{t^2=t^2+1-1}\int_0^1 \frac{t^2+1-1}{1+t^2} d t=\left.\int_0^1 1 d t-\int_0^1 \frac{1}{1+t^2} d t\right]=\left.1-\arctan t\right|_0 ^1\xlongequal[\arctan 0=0]{\arctan 1=\frac{\pi}{4}}1-\frac{\pi}{4} ∫ 0 1 1 + t 2 t 2 d t t 2 = t 2 + 1 − 1 ∫ 0 1 1 + t 2 t 2 + 1 − 1 d t = ∫ 0 1 1 d t − ∫ 0 1 1 + t 2 1 d t ] = 1 − arctan t ∣ 0 1 a r c t a n 1 = 4 π a r c t a n 0 = 0 1 − 4 π 合并整理得: − 4 ⋅ [ ln 2 − 2 ( 1 − π 4 ) ] = − 4 ln 2 + 8 − 2 π -4 \cdot\left[\ln 2-2\left(1-\frac{\pi}{4}\right)\right]=-4 \ln 2+8-2 \pi − 4 ⋅ [ ln 2 − 2 ( 1 − 4 π ) ] = − 4 ln 2 + 8 − 2 π (16) (本题满分 10 分)设数列 { a n } \left\{a_{n}\right\} { a n } a 0 = 3 , a 1 = 1 , a n − 2 − n ( n − 1 ) a n = 0 ( n ⩾ 2 ) . S ( x ) a_{0}=3, a_{1}=1, a_{n-2}-n(n-1) a_{n}=0(n \geqslant 2) . S(x) a 0 = 3 , a 1 = 1 , a n − 2 − n ( n − 1 ) a n = 0 ( n ⩾ 2 ) . S ( x ) ∑ n = 0 ∞ a n x n \displaystyle \sum_{n=0}^{\infty} a_{n} x^{n} n = 0 ∑ ∞ a n x n S ′ ′ ( x ) − S ( x ) = 0 S^{\prime \prime}(x)-S(x)=0 S ′′ ( x ) − S ( x ) = 0 S ( x ) S(x) S ( x )
(16) ( I ) 证法 1 由题设得 a 2 n = 3 ( 2 n ) ! , a 2 n + 1 = 1 ( 2 n + 1 ) ! a_{2 n}=\frac{3}{(2 n) !}, a_{2 n+1}=\frac{1}{(2 n+1) !} a 2 n = ( 2 n )! 3 , a 2 n + 1 = ( 2 n + 1 )! 1 ∑ n = 0 ∞ a n x n \displaystyle \sum_{n=0}^{\infty} a_n x^n n = 0 ∑ ∞ a n x n + ∞ +\infty + ∞ S ( x ) = ∑ n = 0 ∞ a n x n \displaystyle S(x)=\sum_{n=0}^{\infty} a_n x^n S ( x ) = n = 0 ∑ ∞ a n x n S ′ ( x ) = ∑ n = 1 ∞ n a n x n − 1 , S ′ ′ ( x ) = ∑ n = 2 ∞ n ( n − 1 ) a n x n − 2 . \displaystyle S^{\prime}(x)=\sum_{n=1}^{\infty} n a_n x^{n-1}, S^{\prime \prime}(x)=\sum_{n=2}^{\infty} n(n-1) a_n x^{n-2} . S ′ ( x ) = n = 1 ∑ ∞ n a n x n − 1 , S ′′ ( x ) = n = 2 ∑ ∞ n ( n − 1 ) a n x n − 2 . a n − 2 − n ( n − 1 ) a n = 0 a_{n-2}-n(n-1) a_n=0 a n − 2 − n ( n − 1 ) a n = 0 S ′ ′ ( x ) = ∑ n = 2 ∞ a n − 2 x n − 2 = ∑ n = 0 ∞ a n x n \displaystyle S^{\prime \prime}(x)=\sum_{n=2}^{\infty} a_{n-2} x^{n-2}=\sum_{n=0}^{\infty} a_n x^n S ′′ ( x ) = n = 2 ∑ ∞ a n − 2 x n − 2 = n = 0 ∑ ∞ a n x n S ′ ′ ( x ) − S ( x ) = 0 S^{\prime \prime}(x)-S(x)=0 S ′′ ( x ) − S ( x ) = 0 a 2 n = 3 ( 2 n ) ! , a 2 n + 1 = 1 ( 2 n + 1 ) ! a_{2 n}=\frac{3}{(2 n) !}, a_{2 n+1}=\frac{1}{(2 n+1) !} a 2 n = ( 2 n )! 3 , a 2 n + 1 = ( 2 n + 1 )! 1 ∑ n = 0 ∞ a n x n \displaystyle \sum_{n=0}^{\infty} a_n x^n n = 0 ∑ ∞ a n x n + ∞ +\infty + ∞ e x = ∑ n = 0 ∞ x n n ! , e − x = ∑ n = 0 ∞ ( − 1 ) n x n n ! , − ∞ < x < + ∞ , \displaystyle \mathrm{e}^x=\sum_{n=0}^{\infty} \frac{x^n}{n !}, \mathrm{e}^{-x}=\sum_{n=0}^{\infty}(-1)^n \frac{x^n}{n !},-\infty<x<+\infty, e x = n = 0 ∑ ∞ n ! x n , e − x = n = 0 ∑ ∞ ( − 1 ) n n ! x n , − ∞ < x < + ∞ , e x + e − x = 2 ∑ n = 0 ∞ x 2 n ( 2 n ) ! , e x − e − x = 2 ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! , \displaystyle \mathrm{e}^x+\mathrm{e}^{-x}=2 \sum_{n=0}^{\infty} \frac{x^{2 n}}{(2 n) !}, \mathrm{e}^x-\mathrm{e}^{-x}=2 \sum_{n=0}^{\infty} \frac{x^{2 n+1}}{(2 n+1) !}, e x + e − x = 2 n = 0 ∑ ∞ ( 2 n )! x 2 n , e x − e − x = 2 n = 0 ∑ ∞ ( 2 n + 1 )! x 2 n + 1 , S ( x ) = ∑ n = 0 ∞ a n x n = 3 ∑ n = 0 ∞ 1 ( 2 n ) ! x 2 n + ∑ n = 0 ∞ 1 ( 2 n + 1 ) ! x 2 n + 1 \displaystyle \begin{aligned} S(x) & =\sum_{n=0}^{\infty} a_n x^n=3 \sum_{n=0}^{\infty} \frac{1}{(2 n) !} x^{2 n}+\sum_{n=0}^{\infty} \frac{1}{(2 n+1) !} x^{2 n+1} \end{aligned} S ( x ) = n = 0 ∑ ∞ a n x n = 3 n = 0 ∑ ∞ ( 2 n )! 1 x 2 n + n = 0 ∑ ∞ ( 2 n + 1 )! 1 x 2 n + 1 = 3 2 ( e x + e − x ) + 1 2 ( e x − e − x ) \displaystyle \begin{aligned} =\frac{3}{2}\left(\mathrm{e}^x+\mathrm{e}^{-x}\right)+\frac{1}{2}\left(\mathrm{e}^x-\mathrm{e}^{-x}\right) \end{aligned} = 2 3 ( e x + e − x ) + 2 1 ( e x − e − x ) = 2 e x + e − x ( − ∞ < x < + ∞ ) . \displaystyle \begin{aligned} =2 \mathrm{e}^x+\mathrm{e}^{-x}(-\infty<x<+\infty) . \end{aligned} = 2 e x + e − x ( − ∞ < x < + ∞ ) . S ( x ) = 2 e x + e − x S(x)=2 \mathrm{e}^x+\mathrm{e}^{-x} S ( x ) = 2 e x + e − x S ′ ( x ) = 2 e x − e − x , S ′ ′ ( x ) = 2 e x + e − x , S^{\prime}(x)=2 \mathrm{e}^x-\mathrm{e}^{-x}, S^{\prime \prime}(x)=2 \mathrm{e}^x+\mathrm{e}^{-x}, S ′ ( x ) = 2 e x − e − x , S ′′ ( x ) = 2 e x + e − x , S ′ ′ ( x ) − S ( x ) = 0 S^{\prime \prime}(x)-S(x)=0 S ′′ ( x ) − S ( x ) = 0 S ′ ′ ( x ) − S ( x ) = 0 S^{\prime \prime}(x)-S(x)=0 S ′′ ( x ) − S ( x ) = 0 r 2 − 1 = 0 r^2-1=0 r 2 − 1 = 0 S ( x ) = C 1 e x + C 2 e − x . S(x)=C_1 \mathrm{e}^x+C_2 \mathrm{e}^{-x} \text {. } S ( x ) = C 1 e x + C 2 e − x . S ( 0 ) = a 0 = 3 , S ′ ( 0 ) = a 1 = 1 S(0)=a_0=3, S^{\prime}(0)=a_1=1 S ( 0 ) = a 0 = 3 , S ′ ( 0 ) = a 1 = 1 { C 1 + C 2 = 3 , C 1 − C 2 = 1 , \displaystyle \left\{\begin{array}{l}C_1+C_2=3, \\C_1-C_2=1,\end{array}\right. { C 1 + C 2 = 3 , C 1 − C 2 = 1 , C 1 = 2 , C 2 = 1 C_1=2, C_2=1 C 1 = 2 , C 2 = 1 S ( x ) = 2 e x + e − x ( − ∞ < x < + ∞ ) S(x)=2 \mathrm{e}^x+\mathrm{e}^{-x}(-\infty<x<+\infty) S ( x ) = 2 e x + e − x ( − ∞ < x < + ∞ ) (17) (本题满分 10 分)求函数 f ( x , y ) = ( y + x 3 3 ) e x + y f(x, y)=\left(y+\frac{x^{3}}{3}\right) \mathrm{e}^{x+y} f ( x , y ) = ( y + 3 x 3 ) e x + y
(17) 为了解释并展开给定的数学问题和答案成二叉树形式,我们将遵循先序遍历的方式。该问题涉及求函数 f ( x , y ) = ( y + x 3 3 ) e x + y f(x, y) = \left(y + \frac{x^3}{3}\right) \mathrm{e}^{x+y} f ( x , y ) = ( y + 3 x 3 ) e x + y
求函数 f ( x , y ) f(x, y) f ( x , y ) f x ′ ( x , y ) f_x^{\prime}(x, y) f x ′ ( x , y ) f y ′ ( x , y ) f_y^{\prime}(x, y) f y ′ ( x , y )
f x ′ ( x , y ) = ( x 2 + y + x 3 3 ) ⏟ = 0 e x + y f_x^{\prime}(x, y) = \underbrace{\left(x^2 + y + \frac{x^3}{3}\right)}_{=0} \mathrm{e}^{x+y} f x ′ ( x , y ) = = 0 ( x 2 + y + 3 x 3 ) e x + y f y ′ ( x , y ) = ( 1 + y + x 3 3 ) ⏟ = 0 e x + y f_y^{\prime}(x, y) = \underbrace{\left(1 + y + \frac{x^3}{3}\right)}_{=0} \mathrm{e}^{x+y} f y ′ ( x , y ) = = 0 ( 1 + y + 3 x 3 ) e x + y 消元法求驻点 令 f x ′ ( x , y ) = 0 f_x^{\prime}(x, y) = 0 f x ′ ( x , y ) = 0 f y ′ ( x , y ) = 0 f_y^{\prime}(x, y) = 0 f y ′ ( x , y ) = 0 ( − 1 , − 2 3 ) (-1, -\frac{2}{3}) ( − 1 , − 3 2 ) ( 1 , − 4 3 ) (1, -\frac{4}{3}) ( 1 , − 3 4 ) 求函数 f ( x , y ) f(x, y) f ( x , y )
A = f x x ′ ′ ( x , y ) = ( x 2 + y + x 3 3 ) x ′ = 2 x + x 2 e x + y ( y + x 3 3 + 2 x 2 + 2 x ) A = f_{xx}^{\prime\prime}(x, y) \xlongequal[]{\left(x^2+y+\frac{x^3}{3}\right)_x^{\prime}=2 x+x^2}\mathrm{e}^{x+y}\left(y + \frac{x^3}{3} + 2x^2 + 2x\right) A = f xx ′′ ( x , y ) ( x 2 + y + 3 x 3 ) x ′ = 2 x + x 2 e x + y ( y + 3 x 3 + 2 x 2 + 2 x ) B = f x y ′ ′ ( x , y ) = ( x 2 + y + x 3 3 ) y ′ = 1 e x + y ( y + x 3 3 + x 2 + 1 ) B = f_{xy}^{\prime\prime}(x, y) \xlongequal[]{\left(x^2+y+\frac{x^3}{3}\right)^{\prime}_y=1}\mathrm{e}^{x+y}\left(y + \frac{x^3}{3} + x^2 + 1\right) B = f x y ′′ ( x , y ) ( x 2 + y + 3 x 3 ) y ′ = 1 e x + y ( y + 3 x 3 + x 2 + 1 ) C = f y y ′ ′ ( x , y ) = ( 1 + y + x 3 3 ) y ′ = 1 e x + y ( y + x 3 3 + 2 ) C = f_{yy}^{\prime\prime}(x, y) \xlongequal[]{\left(1+y+\frac{x^3}{3}\right)^{\prime}_y=1} \mathrm{e}^{x+y}\left(y + \frac{x^3}{3} + 2\right) C = f yy ′′ ( x , y ) ( 1 + y + 3 x 3 ) y ′ = 1 e x + y ( y + 3 x 3 + 2 ) 判断极值类型。
在点 ( − 1 , − 2 3 ) (-1, -\frac{2}{3}) ( − 1 , − 3 2 ) A C − B 2 AC - B^2 A C − B 2 A = e − 5 3 ⋅ ( − 2 3 − 1 3 + 2 − 2 ) = − e − 5 3 A=e^{-\frac{5}{3}} \cdot\left(-\frac{2}{3}-\frac{1}{3}+2-2\right)=-e^{-\frac{5}{3}} A = e − 3 5 ⋅ ( − 3 2 − 3 1 + 2 − 2 ) = − e − 3 5 B = e − 5 3 ⋅ ( − 2 3 − 1 3 + 1 + 1 ) = e − 5 3 B=e^{-\frac{5}{3}} \cdot\left(-\frac{2}{3}-\frac{1}{3}+1+1\right)=e^{-\frac{5}{3}} B = e − 3 5 ⋅ ( − 3 2 − 3 1 + 1 + 1 ) = e − 3 5 C = e − 5 3 ⋅ ( − 2 3 − 1 3 + 2 ) = e − 5 3 C=e^{-\frac{5}{3}} \cdot\left(-\frac{2}{3}-\frac{1}{3}+2\right)=e^{-\frac{5}{3}} C = e − 3 5 ⋅ ( − 3 2 − 3 1 + 2 ) = e − 3 5 由于 A C − B 2 < 0 AC - B^2 < 0 A C − B 2 < 0 ( − 1 , − 2 3 ) (-1, -\frac{2}{3}) ( − 1 , − 3 2 ) 在点 ( 1 , − 4 3 ) (1, -\frac{4}{3}) ( 1 , − 3 4 ) A C − B 2 AC - B^2 A C − B 2 A = e − 1 3 ⋅ ( − 4 3 + 1 3 + 2 + 2 ) = 3 e − 1 3 A=e^{-\frac{1}{3}} \cdot\left(-\frac{4}{3}+\frac{1}{3}+2+2\right)=3 e^{-\frac{1}{3}} A = e − 3 1 ⋅ ( − 3 4 + 3 1 + 2 + 2 ) = 3 e − 3 1 B = e − 1 3 ⋅ ( − 4 3 + 1 3 + 1 + 1 ) = 1 B=e^{-\frac{1}{3}} \cdot\left(-\frac{4}{3}+\frac{1}{3}+1+1\right)=1 B = e − 3 1 ⋅ ( − 3 4 + 3 1 + 1 + 1 ) = 1 c = e − 1 3 ⋅ ( − 4 3 + 1 3 + 2 ) = 1 c=e^{-\frac{1}{3}} \cdot\left(-\frac{4}{3}+\frac{1}{3}+2\right)=1 c = e − 3 1 ⋅ ( − 3 4 + 3 1 + 2 ) = 1 由于 A C − B 2 > 0 AC - B^2 > 0 A C − B 2 > 0 A > 0 A > 0 A > 0 ( 1 , − 4 3 ) (1, -\frac{4}{3}) ( 1 , − 3 4 ) 计算极小值。
极小值为 f ( 1 , − 4 3 ) = − e − 1 3 f(1, -\frac{4}{3}) = -\mathrm{e}^{-\frac{1}{3}} f ( 1 , − 3 4 ) = − e − 3 1 (18) (本题满分 10 分)设奇函数 f ( x ) f(x) f ( x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] f ( 1 ) = 1 f(1)=1 f ( 1 ) = 1 ξ ∈ ( 0 , 1 ) \xi \in(0,1) ξ ∈ ( 0 , 1 ) f ′ ( ξ ) = 1 f^{\prime}(\xi)=1 f ′ ( ξ ) = 1 η ∈ ( − 1 , 1 ) \eta \in(-1,1) η ∈ ( − 1 , 1 ) f ′ ′ ( η ) + f ′ ( η ) = 1 f^{\prime \prime}(\eta)+f^{\prime}(\eta)=1 f ′′ ( η ) + f ′ ( η ) = 1
(18) (I) 证法 1 因为 f ( x ) f(x) f ( x ) f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ] f ( 1 ) = 1 f(1)=1 f ( 1 ) = 1 ξ ∈ ( 0 , 1 ) \xi \in(0,1) ξ ∈ ( 0 , 1 ) f ′ ( ξ ) = f ( 1 ) − f ( 0 ) = 1 f^{\prime}(\xi)=f(1)-f(0)=1 f ′ ( ξ ) = f ( 1 ) − f ( 0 ) = 1 F ( x ) = f ( x ) − x F(x)=f(x)-x F ( x ) = f ( x ) − x F ( 0 ) = f ( 0 ) = 0 , F ( 1 ) = f ( 1 ) − 1 = 0 F(0)=f(0)=0, F(1)=f(1)-1=0 F ( 0 ) = f ( 0 ) = 0 , F ( 1 ) = f ( 1 ) − 1 = 0 ξ ∈ \xi \in ξ ∈ ( 0 , 1 ) (0,1) ( 0 , 1 ) F ′ ( ξ ) = 0 F^{\prime}(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) = 1 f^{\prime}(\xi)=1 f ′ ( ξ ) = 1 f ( x ) f(x) f ( x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] f ′ ( x ) f^{\prime}(x) f ′ ( x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] f ′ ( − ξ ) = f ′ ( ξ ) = 1 . f^{\prime}(-\xi)=f^{\prime}(\xi)=1 \text {. } f ′ ( − ξ ) = f ′ ( ξ ) = 1 . F ( x ) = [ f ′ ( x ) − 1 ] e x F(x)=\left[f^{\prime}(x)-1\right] \mathrm{e}^x F ( x ) = [ f ′ ( x ) − 1 ] e x F ( x ) F(x) F ( x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] F ( − ξ ) = F ( ξ ) = 0 F(-\xi)=F(\xi)=0 F ( − ξ ) = F ( ξ ) = 0 η ∈ ( − ξ , ξ ) ⊂ ( − 1 , 1 ) \eta \in(-\xi, \xi) \subset(-1,1) η ∈ ( − ξ , ξ ) ⊂ ( − 1 , 1 ) F ′ ( η ) = 0 F^{\prime}(\eta)=0 F ′ ( η ) = 0 F ′ ( η ) = [ f ′ ′ ( η ) + f ′ ( η ) − 1 ] e η 且 e η ≠ 0 , F^{\prime}(\eta)=\left[f^{\prime \prime}(\eta)+f^{\prime}(\eta)-1\right] \mathrm{e}^\eta \text { 且 } \mathrm{e}^\eta \neq 0, F ′ ( η ) = [ f ′′ ( η ) + f ′ ( η ) − 1 ] e η 且 e η = 0 , f ′ ′ ( η ) + f ′ ( η ) = 1 f^{\prime \prime}(\eta)+f^{\prime}(\eta)=1 f ′′ ( η ) + f ′ ( η ) = 1 证法2 因为 f ( x ) f(x) f ( x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] , , , f ′ ( x ) f^{\prime}(x) f ′ ( x ) . . . F ( x ) = f ′ ( x ) + f ( x ) − x , F(x)=f^{\prime}(x)+f(x)-x, F ( x ) = f ′ ( x ) + f ( x ) − x , F ( x ) F(x) F ( x ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] , , , − F ( 1 ) = f ′ ( 1 ) + f ( 1 ) − 1 = f ′ ( 1 ) , − F ( − 1 ) = f ′ ( − 1 ) + f ( − 1 ) + 1 = f ′ ( 1 ) − f ( 1 ) + 1 = f ′ ( 1 ) , -\displaystyle \begin{aligned} F(1)=f^{\prime}(1)+f(1)-1=f^{\prime}(1), \end{aligned}-\displaystyle \begin{aligned} F(-1)=f^{\prime}(-1)+f(-1)+1=f^{\prime}(1)-f(1)+1=f^{\prime}(1), \end{aligned} − F ( 1 ) = f ′ ( 1 ) + f ( 1 ) − 1 = f ′ ( 1 ) , − F ( − 1 ) = f ′ ( − 1 ) + f ( − 1 ) + 1 = f ′ ( 1 ) − f ( 1 ) + 1 = f ′ ( 1 ) , , , , η ∈ ( − 1 , 1 ) , \eta \in(-1,1), η ∈ ( − 1 , 1 ) , F ′ ( η ) = 0. F^{\prime}(\eta)=0. F ′ ( η ) = 0. F ′ ( x ) = f ′ ′ ( x ) + f ′ ( x ) − 1 , F^{\prime}(x)=f^{\prime \prime}(x)+f^{\prime}(x)-1, F ′ ( x ) = f ′′ ( x ) + f ′ ( x ) − 1 , f ′ ′ ( η ) + f ′ ( η ) − 1 = 0 , f^{\prime \prime}(\eta)+f^{\prime}(\eta)-1=0, f ′′ ( η ) + f ′ ( η ) − 1 = 0 , f ′ ′ ( η ) + f ′ ( η ) = 1 f^{\prime \prime}(\eta)+f^{\prime}(\eta)=1 f ′′ ( η ) + f ′ ( η ) = 1 (19) (本题满分 10 分)
设直线 L L L A ( 1 , 0 , 0 ) , B ( 0 , 1 , 1 ) A(1,0,0), B(0,1,1) A ( 1 , 0 , 0 ) , B ( 0 , 1 , 1 ) L L L z z z Σ , Σ \displaystyle \Sigma, \Sigma Σ , Σ z = 0 , z = 2 z=0, z=2 z = 0 , z = 2 Ω \Omega Ω Σ \displaystyle \Sigma Σ Ω \Omega Ω
(19) 曲面求法1 由 A ( 1 , 0 , 0 ) , B ( 0 , 1 , 1 ) A(1,0,0), B(0,1,1) A ( 1 , 0 , 0 ) , B ( 0 , 1 , 1 ) A B → = ( − 1 , 1 , 1 ) \overrightarrow{A B}=(-1,1,1) A B = ( − 1 , 1 , 1 ) 直线 L L L x − 1 1 = y − 1 = z − 1 \displaystyle \begin{aligned}\frac{x-1}{1}=\frac{y}{-1}=\frac{z}{-1}\end{aligned} 1 x − 1 = − 1 y = − 1 z x − 1 − 1 = z ⇒ x = 1 − z \displaystyle \begin{aligned} & \frac{x-1}{-1}=z \Rightarrow x=1-z \end{aligned} − 1 x − 1 = z ⇒ x = 1 − z y 1 = z 1 ⇒ y = z . \displaystyle \begin{aligned} \frac{y}{1}=\frac{z}{1} \Rightarrow y=z . \end{aligned} 1 y = 1 z ⇒ y = z . 从而曲面 Σ \displaystyle \Sigma Σ x 2 + y 2 = ( 1 − z ) 2 + z 2 x^2+y^2=(1-z)^2+z^2 x 2 + y 2 = ( 1 − z ) 2 + z 2 即 x 2 + y 2 = 2 z 2 − 2 z + 1 x^2+y^2=2 z^2-2 z+1 x 2 + y 2 = 2 z 2 − 2 z + 1 曲面求法2 L : x − 1 − 1 = y 1 = z 1 = t \displaystyle \begin{aligned} & L: \frac{x-1}{-1}=\frac{y}{1}=\frac{z}{1}=t \end{aligned} L : − 1 x − 1 = 1 y = 1 z = t { x = 1 − t y = t z = t ⇒ Σ : x 2 + y 2 = ( 1 − t ) 2 + t 2 = ( 1 − z ) 2 + z 2 \displaystyle \begin{aligned} \left\{\begin{array}{l}x=1-t \\y=t \\z=t\end{array} \Rightarrow \Sigma: x^2+y^2=(1-t)^2+t^2=(1-z)^2+z^2\right. \end{aligned} ⎩ ⎨ ⎧ x = 1 − t y = t z = t ⇒ Σ : x 2 + y 2 = ( 1 − t ) 2 + t 2 = ( 1 − z ) 2 + z 2 从而曲面 Σ \displaystyle \Sigma Σ x 2 + y 2 = ( 1 − z ) 2 + z 2 x^2+y^2=(1-z)^2+z^2 x 2 + y 2 = ( 1 − z ) 2 + z 2 即 x 2 + y 2 = 2 z 2 − 2 z + 1 x^2+y^2=2 z^2-2 z+1 x 2 + y 2 = 2 z 2 − 2 z + 1 x 2 + y 2 − 2 ( z − 1 2 ) 2 = 1 2 x^2+y^2-2\left(z-\frac{1}{2}\right)^2=\frac{1}{2} x 2 + y 2 − 2 ( z − 2 1 ) 2 = 2 1 第二问
(II) 设 Ω \Omega Ω ( x ˉ , y ˉ , z ˉ ) (\bar{x}, \bar{y}, \bar{z}) ( x ˉ , y ˉ , z ˉ )
由曲面 Σ \displaystyle \Sigma Σ Ω \Omega Ω x O z , y O z x O z, y O z x O z , y O z x x x y y y x ˉ = ∭ Ω x d x d y d z ∭ Ω d x d y d z = 0 , \displaystyle \begin{aligned}\bar{x}=\frac{\iiint_{\Omega} x \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}=0,\end{aligned} x ˉ = ∭ Ω d x d y d z ∭ Ω x d x d y d z = 0 , y ˉ = ∭ Ω y d x d y d z ∭ Ω d x d y d z = 0 \displaystyle \begin{aligned}\bar{y}=\frac{\iiint_{\Omega} y \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}=0\end{aligned} y ˉ = ∭ Ω d x d y d z ∭ Ω y d x d y d z = 0 接下来求z z z
坐标取值范围 D z = { ( x , y ) ∣ x 2 + y 2 ⩽ 2 z 2 − 2 z + 1 } \displaystyle \begin{aligned} & D_z=\left\{(x, y) \mid x^2+y^2 \leqslant 2 z^2-2 z+1\right\} \end{aligned} D z = { ( x , y ) ∣ x 2 + y 2 ⩽ 2 z 2 − 2 z + 1 } 面积是π r 2 = π \cdotp 2 z 2 − 2 z + 1 \displaystyle \begin{aligned} \pi r^2=\pi\text{·}2 z^2-2 z+1\end{aligned} π r 2 = π \cdotp 2 z 2 − 2 z + 1 Ω = { ( x , y , z ) ∣ ( x , y ) ∈ D z , 0 ≤ z ⩽ 2 } \displaystyle \begin{aligned} \Omega=\left\{(x, y, z) \mid(x, y) \in D_z, 0 \leq z \leqslant 2\right\} \end{aligned} Ω = { ( x , y , z ) ∣ ( x , y ) ∈ D z , 0 ≤ z ⩽ 2 } z ˉ = ∭ Ω z d x d y d z ∭ Ω d x d y d z = 0 \displaystyle \begin{aligned}\bar{z}=\frac{\iiint_{\Omega} z\mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}=0\end{aligned} z ˉ = ∭ Ω d x d y d z ∭ Ω z d x d y d z = 0 ∭ Ω z d x d y d z = ∫ 0 2 z d z ∬ D z d x d y = ∫ 0 2 z ⋅ π ( 2 z 2 − 2 z + 1 ) d z = 14 3 π , \displaystyle \begin{aligned} & \iiint_{\Omega} z \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z=\int_0^2 z \mathrm{~d} z \iint_{D_z} \mathrm{~d} x \mathrm{~d} y=\int_0^2 z \cdot \pi\left(2 z^2-2 z+1\right) \mathrm{d} z=\frac{14}{3} \pi, \end{aligned} ∭ Ω z d x d y d z = ∫ 0 2 z d z ∬ D z d x d y = ∫ 0 2 z ⋅ π ( 2 z 2 − 2 z + 1 ) d z = 3 14 π , ∭ Ω d x d y d z = ∫ 0 2 d z ∬ D z d x d y = ∫ 0 2 π ( 2 z 2 − 2 z + 1 ) d z = 10 3 π . \displaystyle \begin{aligned} \iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z=\int_0^2 \mathrm{~d} z \iint_{D_z} \mathrm{~d} x \mathrm{~d} y=\int_0^2 \pi\left(2 z^2-2 z+1\right) \mathrm{d} z=\frac{10}{3} \pi . \end{aligned} ∭ Ω d x d y d z = ∫ 0 2 d z ∬ D z d x d y = ∫ 0 2 π ( 2 z 2 − 2 z + 1 ) d z = 3 10 π . 于是
z ˉ = ∬ Ω z d x d y d z ∭ Ω d x d y d z = 7 5 \displaystyle \begin{aligned}\bar{z}=\frac{\iint_{\Omega} z \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}=\frac{7}{5}\end{aligned} z ˉ = ∭ Ω d x d y d z ∬ Ω z d x d y d z = 5 7 因此,Ω \Omega Ω ( 0 , 0 , 7 5 ) \left(0,0, \frac{7}{5}\right) ( 0 , 0 , 5 7 ) 空间区域的形心:空间有界闭区域 Ω \Omega Ω x ˉ = 1 V ∭ Ω x d v , y ˉ = 1 V ∭ Ω y d v , z ˉ = 1 V ∭ Ω z d v , \displaystyle \begin{aligned} \bar{x} & =\frac{1}{V} \iiint_{\Omega} x \mathrm{~d} v, \\\bar{y} & =\frac{1}{V} \iiint_{\Omega} y \mathrm{~d} v, \\\bar{z} & =\frac{1}{V} \iiint_{\Omega} z \mathrm{~d} v, \end{aligned} x ˉ y ˉ z ˉ = V 1 ∭ Ω x d v , = V 1 ∭ Ω y d v , = V 1 ∭ Ω z d v ,
其中 V = ∭ Ω d v V=\iiint_{\Omega} \mathrm{d} v V = ∭ Ω d v Ω \Omega Ω 设 Ω \Omega Ω Ω \Omega Ω ( x ˉ , y ˉ , z ˉ ) = ( ∭ Ω x d x d y d z ∭ Ω d x d y d z , ∭ Ω y d x d y d z ∭ Ω d x d y d z , ∬ Ω z d x d y d z ∭ Ω d x d y d z ) (\bar{x}, \bar{y}, \bar{z})=\left(\frac{\iiint_{\Omega} x \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}, \frac{\iiint_{\Omega} y \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}, \frac{\iint_{\Omega} z \mathrm{~d} x \mathrm{~d} y \mathrm{~d} z}{\iiint_{\Omega} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z}\right) ( x ˉ , y ˉ , z ˉ ) = ( ∭ Ω d x d y d z ∭ Ω x d x d y d z , ∭ Ω d x d y d z ∭ Ω y d x d y d z , ∭ Ω d x d y d z ∬ Ω z d x d y d z ) (20) (本题满分 11 分)
设 A = ( 1 a 1 0 ) , B = ( 0 1 1 b ) \displaystyle \boldsymbol{A}=\left(\begin{array}{ll}1 & a \\ 1 & 0\end{array}\right), \boldsymbol{B}=\left(\begin{array}{ll}0 & 1 \\ 1 & b\end{array}\right) A = ( 1 1 a 0 ) , B = ( 0 1 1 b ) a , b a, b a , b C \boldsymbol{C} C A C − C A = B \boldsymbol{A C}-\boldsymbol{C A}=\boldsymbol{B} AC − CA = B C \boldsymbol{C} C
(20) 解 设矩阵 C = ( x 1 x 2 x 3 x 4 ) \displaystyle \boldsymbol{C}=\left(\begin{array}{ll}x_1 & x_2 \\ x_3 & x_4\end{array}\right) C = ( x 1 x 3 x 2 x 4 ) A C − C A = B \boldsymbol{A C}-\boldsymbol{C A}=\boldsymbol{B} AC − CA = B { − x 2 + a x 3 = 0 − a x 1 + x 2 + a x 4 = 1 x 1 − x 3 − x 4 = 1 x 2 − a x 3 = b . 对该方程组的增广矩阵作初等行变换 \displaystyle \left\{\begin{array}{l}-x_2+a x_3=0 \\-a x_1+x_2+a x_4=1 \\x_1-x_3-x_4=1 \\x_2-a x_3=b .\end{array}\right.\text{对该方程组的增广矩阵作初等行变换} ⎩ ⎨ ⎧ − x 2 + a x 3 = 0 − a x 1 + x 2 + a x 4 = 1 x 1 − x 3 − x 4 = 1 x 2 − a x 3 = b . 对该方程组的增广矩阵作初等行变换 ( 0 − 1 a 0 0 − a 1 0 a 1 1 0 − 1 − 1 1 0 1 − a 0 b ) → ( 1 0 − 1 − 1 1 0 1 − a 0 0 0 0 0 0 a + 1 0 0 0 0 b ) . \displaystyle \left(\begin{array}{cccc:c}0 & -1 & a & 0 & 0 \\-a & 1 & 0 & a & 1 \\1 & 0 & -1 & -1 & 1 \\0 & 1 & -a & 0 & b\end{array}\right) \rightarrow\left(\begin{array}{cccc:c}1 & 0 & -1 & -1 & 1 \\0 & 1 & -a & 0 & 0 \\0 & 0 & 0 & 0 & a+1 \\0 & 0 & 0 & 0 & b\end{array}\right) . 0 − a 1 0 − 1 1 0 1 a 0 − 1 − a 0 a − 1 0 0 1 1 b → 1 0 0 0 0 1 0 0 − 1 − a 0 0 − 1 0 0 0 1 0 a + 1 b . a ≠ − 1 a \neq-1 a = − 1 b ≠ 0 b \neq 0 b = 0 a = − 1 a=-1 a = − 1 b = 0 b=0 b = 0 a = − 1 a=-1 a = − 1 b = 0 b=0 b = 0 C C C C = ( 1 + k 1 + k 2 − k 1 k 1 k 2 ) \displaystyle C=\left(\begin{array}{cc}1+k_1+k_2 & -k_1 \\ k_1 & k_2\end{array}\right) C = ( 1 + k 1 + k 2 k 1 − k 1 k 2 ) k 1 , k 2 k_1, k_2 k 1 , k 2 C \boldsymbol{C} C (21) (本题满分 11 分)
设二次型 f ( x 1 , x 2 , x 3 ) = 2 ( a 1 x 1 + a 2 x 2 + a 3 x 3 ) 2 + ( b 1 x 1 + b 2 x 2 + b 3 x 3 ) 2 f\left(x_{1}, x_{2}, x_{3}\right)=2\left(a_{1} x_{1}+a_{2} x_{2}+a_{3} x_{3}\right)^{2}+\left(b_{1} x_{1}+b_{2} x_{2}+b_{3} x_{3}\right)^{2} f ( x 1 , x 2 , x 3 ) = 2 ( a 1 x 1 + a 2 x 2 + a 3 x 3 ) 2 + ( b 1 x 1 + b 2 x 2 + b 3 x 3 ) 2
α = ( a 1 a 2 a 3 ) , β = ( b 1 b 2 b 3 ) . \displaystyle \boldsymbol{\alpha}=\left(\begin{array}{l}a_{1} \\a_{2} \\a_{3}\end{array}\right), \quad \boldsymbol{\beta}=\left(\begin{array}{l}b_{1} \\b_{2} \\b_{3}\end{array}\right) . α = a 1 a 2 a 3 , β = b 1 b 2 b 3 . f f f 2 α α T + β β T 2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} 2 α α T + β β T (II) 若 α , β \boldsymbol{\alpha}, \boldsymbol{\beta} α , β f f f 2 y 1 2 + y 2 2 2 y_{1}^{2}+y_{2}^{2} 2 y 1 2 + y 2 2
(21) (I ) 证法 1 记列向量 x = ( x 1 x 2 x 3 ) \displaystyle \boldsymbol{x}=\left(\begin{array}{l}x_1 \\ x_2 \\ x_3\end{array}\right) x = x 1 x 2 x 3 a 1 x 1 + a 2 x 2 + a 3 x 3 = ( x 1 , x 2 , x 3 ) ( a 1 a 2 a 3 ) = ( a 1 , a 2 , a 3 ) ( x 1 x 2 x 3 ) , \displaystyle a_1 x_1+a_2 x_2+a_3 x_3=\left(x_1, x_2, x_3\right)\left(\begin{array}{l}a_1 \\a_2 \\a_3\end{array}\right)=\left(a_1, a_2, a_3\right)\left(\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right), a 1 x 1 + a 2 x 2 + a 3 x 3 = ( x 1 , x 2 , x 3 ) a 1 a 2 a 3 = ( a 1 , a 2 , a 3 ) x 1 x 2 x 3 , b 1 x 1 + b 2 x 2 + b 3 x 3 b_1 x_1+b_2 x_2+b_3 x_3 b 1 x 1 + b 2 x 2 + b 3 x 3 f ( x 1 , x 2 , x 3 ) = 2 ( a 1 x 1 + a 2 x 2 + a 3 x 3 ) 2 + ( b 1 x 1 + b 2 x 2 + b 3 x 3 ) 2 \displaystyle \begin{aligned} f\left(x_1, x_2, x_3\right) & =2\left(a_1 x_1+a_2 x_2+a_3 x_3\right)^2+\left(b_1 x_1+b_2 x_2+b_3 x_3\right)^2 \end{aligned} f ( x 1 , x 2 , x 3 ) = 2 ( a 1 x 1 + a 2 x 2 + a 3 x 3 ) 2 + ( b 1 x 1 + b 2 x 2 + b 3 x 3 ) 2 = 2 ( x 1 , x 2 , x 3 ) ( a 1 a 2 a 3 ) ( a 1 , a 2 , a 3 ) ( x 1 x 2 x 3 ) + ( x 1 , x 2 , x 3 ) ( b 1 b 2 b 3 ) ( b 1 , b 2 , b 3 ) ( x 1 x 2 x 3 ) \displaystyle \begin{aligned} =2\left(x_1, x_2, x_3\right)\left(\begin{array}{l}a_1 \\a_2 \\a_3\end{array}\right)\left(a_1, a_2, a_3\right)\left(\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right)+\left(x_1, x_2, x_3\right)\left(\begin{array}{l}b_1 \\b_2 \\b_3\end{array}\right)\left(b_1, b_2, b_3\right)\left(\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right) \end{aligned} = 2 ( x 1 , x 2 , x 3 ) a 1 a 2 a 3 ( a 1 , a 2 , a 3 ) x 1 x 2 x 3 + ( x 1 , x 2 , x 3 ) b 1 b 2 b 3 ( b 1 , b 2 , b 3 ) x 1 x 2 x 3 = 2 x T α α T x + x T β β T x = x T ( 2 α α T + β β T ) x , \displaystyle \begin{aligned} =2 \boldsymbol{x}^{\mathrm{T}} \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} \boldsymbol{x}+\boldsymbol{x}^{\mathrm{T}} \boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{x}=\boldsymbol{x}^{\mathrm{T}}\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right) \boldsymbol{x}, \end{aligned} = 2 x T α α T x + x T β β T x = x T ( 2 α α T + β β T ) x , ( 2 α α T + β β T ) T = 2 α α T + β β T \left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right)^{\mathrm{T}}=2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} ( 2 α α T + β β T ) T = 2 α α T + β β T 2 α α T + β β T 2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} 2 α α T + β β T f f f 2 α α T + β β T 2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} 2 α α T + β β T f f f f ( x 1 , x 2 , x 3 ) = 2 ( x 1 , x 2 , x 3 ) ( a 1 2 a 1 a 2 a 1 a 3 a 1 a 2 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 ) ( x 1 x 2 x 3 ) + ( x 1 , x 2 , x 3 ) ( b 1 2 b 1 b 2 b 1 b 3 b 1 b 2 b 2 2 b 2 b 3 b 1 b 3 b 2 b 3 b 3 2 ) ( x 1 x 2 x 3 ) , \displaystyle \begin{aligned} & f\left(x_1, x_2, x_3\right)=2\left(x_1, x_2, x_3\right)\left(\begin{array}{ccc}a_1^2 & a_1 a_2 & a_1 a_3 \\a_1 a_2 & a_2^2 & a_2 a_3 \\a_1 a_3 & a_2 a_3 & a_3^2\end{array}\right)\left(\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right)+\left(x_1, x_2, x_3\right)\left(\begin{array}{ccc}b_1^2 & b_1 b_2 & b_1 b_3 \\b_1 b_2 & b_2^2 & b_2 b_3 \\b_1 b_3 & b_2 b_3 & b_3^2\end{array}\right)\left(\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right), \end{aligned} f ( x 1 , x 2 , x 3 ) = 2 ( x 1 , x 2 , x 3 ) a 1 2 a 1 a 2 a 1 a 3 a 1 a 2 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 x 1 x 2 x 3 + ( x 1 , x 2 , x 3 ) b 1 2 b 1 b 2 b 1 b 3 b 1 b 2 b 2 2 b 2 b 3 b 1 b 3 b 2 b 3 b 3 2 x 1 x 2 x 3 , ( a 1 2 a 1 a 2 a 1 a 3 a 1 a 2 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 ) = ( a 1 a 2 a 3 ) ( a 1 , a 2 , a 3 ) = α α T , \displaystyle \begin{aligned} \left(\begin{array}{ccc}a_1^2 & a_1 a_2 & a_1 a_3 \\a_1 a_2 & a_2^2 & a_2 a_3 \\a_1 a_3 & a_2 a_3 & a_3^2\end{array}\right)=\left(\begin{array}{l}a_1 \\a_2 \\a_3\end{array}\right)\left(a_1, a_2, a_3\right)=\boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}, \end{aligned} a 1 2 a 1 a 2 a 1 a 3 a 1 a 2 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 = a 1 a 2 a 3 ( a 1 , a 2 , a 3 ) = α α T , ( b 1 2 b 1 b 2 b 1 b 3 b 1 b 2 b 2 2 b 2 b 3 b 1 b 3 b 2 b 3 b 3 2 ) = ( b 1 b 2 b 3 ) ( b 1 , b 2 , b 3 ) = β β T , \displaystyle \begin{aligned} \left(\begin{array}{ccc}b_1^2 & b_1 b_2 & b_1 b_3 \\b_1 b_2 & b_2^2 & b_2 b_3 \\b_1 b_3 & b_2 b_3 & b_3^2\end{array}\right)=\left(\begin{array}{l}b_1 \\b_2 \\b_3\end{array}\right)\left(b_1, b_2, b_3\right)=\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T},} \end{aligned} b 1 2 b 1 b 2 b 1 b 3 b 1 b 2 b 2 2 b 2 b 3 b 1 b 3 b 2 b 3 b 3 2 = b 1 b 2 b 3 ( b 1 , b 2 , b 3 ) = β β T , ( a 1 2 a 1 a 2 a 1 a 3 a 1 a 2 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 ) = ( a 1 a 2 a 3 ) ( a 1 , a 2 , a 3 ) = α α T \displaystyle \left(\begin{array}{ccc}a_1^2 & a_1 a_2 & a_1 a_3 \\ a_1 a_2 & a_2^2 & a_2 a_3 \\ a_1 a_3 & a_2 a_3 & a_3^2\end{array}\right)=\left(\begin{array}{l}a_1 \\ a_2 \\ a_3\end{array}\right)\left(a_1, a_2, a_3\right)=\boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} a 1 2 a 1 a 2 a 1 a 3 a 1 a 2 a 2 2 a 2 a 3 a 1 a 3 a 2 a 3 a 3 2 = a 1 a 2 a 3 ( a 1 , a 2 , a 3 ) = α α T ( b 1 2 b 1 b 2 b 1 b 3 b 1 b 2 b 2 2 b 2 b 3 b 1 b 3 b 2 b 3 b 3 2 ) = ( b 1 b 2 b 3 ) ( b 1 , b 2 , b 3 ) = β T , \displaystyle \left(\begin{array}{ccc}b_1^2 & b_1 b_2 & b_1 b_3 \\b_1 b_2 & b_2^2 & b_2 b_3 \\b_1 b_3 & b_2 b_3 & b_3^2\end{array}\right)=\left(\begin{array}{l}b_1 \\b_2 \\b_3\end{array}\right)\left(b_1, b_2, b_3\right)=\boldsymbol{\beta}^{\mathrm{T}}, b 1 2 b 1 b 2 b 1 b 3 b 1 b 2 b 2 2 b 2 b 3 b 1 b 3 b 2 b 3 b 3 2 = b 1 b 2 b 3 ( b 1 , b 2 , b 3 ) = β T , f ( x 1 , x 2 , x 3 ) = ( x 1 , x 2 , x 3 ) ( 2 α α T + β β T ) ( x 1 x 2 x 3 ) , \displaystyle f\left(x_1, x_2, x_3\right)=\left(x_1, x_2, x_3\right)\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right)\left(\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right), f ( x 1 , x 2 , x 3 ) = ( x 1 , x 2 , x 3 ) ( 2 α α T + β β T ) x 1 x 2 x 3 , ( 2 α α T + β β T ) T = 2 α α T + β β T \left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right)^{\mathrm{T}}=2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} ( 2 α α T + β β T ) T = 2 α α T + β β T 2 α α T + β β T 2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} 2 α α T + β β T f f f 2 α α T + β β T 2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} 2 α α T + β β T A = 2 α α T + β β T \boldsymbol{A}=2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}} A = 2 α α T + β β T α , β \boldsymbol{\alpha}, \boldsymbol{\beta} α , β α T α = β T β = 1 , α T β = β T α = \boldsymbol{\alpha}^{\mathrm{T}} \boldsymbol{\alpha}=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\beta}=1, \boldsymbol{\alpha}^{\mathrm{T}} \boldsymbol{\beta}=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\alpha}= α T α = β T β = 1 , α T β = β T α = A α = ( 2 α α T + β β T ) α = 2 α , \displaystyle \begin{aligned} A \boldsymbol{\alpha}=\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right) \boldsymbol{\alpha}=2 \boldsymbol{\alpha}, \end{aligned} A α = ( 2 α α T + β β T ) α = 2 α , A β = ( 2 α α T + β β T ) β = β , \displaystyle \begin{aligned} \boldsymbol{A} \boldsymbol{\beta}=\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right) \boldsymbol{\beta}=\boldsymbol{\beta}, \end{aligned} A β = ( 2 α α T + β β T ) β = β , λ 1 = 2 , λ 2 = 1 \lambda_1=2, \lambda_2=1 λ 1 = 2 , λ 2 = 1 A \boldsymbol{A} A r ( A ) = r ( 2 α α T + β β T ) ⩽ r ( 2 α α T ) + r ( β β T ) = 2 , r(\boldsymbol{A})=r\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right) \leqslant r\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}\right)+r\left(\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right)=2, r ( A ) = r ( 2 α α T + β β T ) ⩽ r ( 2 α α T ) + r ( β β T ) = 2 , A \boldsymbol{A} A λ 3 = 0 \lambda_3=0 λ 3 = 0 A \boldsymbol{A} A f f f 2 y 1 2 + y 2 2 2 y_1^2+y_2^2 2 y 1 2 + y 2 2 λ 1 = 2 , λ 2 = 1 \lambda_1=2, \lambda_2=1 λ 1 = 2 , λ 2 = 1 A \boldsymbol{A} A α , β \boldsymbol{\alpha}, \boldsymbol{\beta} α , β γ \boldsymbol{\gamma} γ α , β \boldsymbol{\alpha}, \boldsymbol{\beta} α , β α T γ = 0 , β T γ = 0 \boldsymbol{\alpha}^{\mathrm{T}} \boldsymbol{\gamma}=0, \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{\gamma}=0 α T γ = 0 , β T γ = 0 Q = ( α , β , γ ) Q=(\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}) Q = ( α , β , γ ) Q Q Q x = Q y ( y = ( y 1 , y 2 , y 3 ) T ) x=Q y\left(y=\left(y_1, y_2, y_3\right)^{\mathrm{T}}\right) x = Q y ( y = ( y 1 , y 2 , y 3 ) T ) f ( x 1 , x 2 , x 3 ) = y T Q T ( 2 α α T + β β T ) Q y = y T ( α T β T γ T ) ( 2 α α T + β β T ) ( α , β , γ ) y \displaystyle \begin{aligned} f\left(x_1, x_2, x_3\right) & =y^{\mathrm{T}} Q^{\mathrm{T}}\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right) Q \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}}\left(\begin{array}{l}\boldsymbol{\alpha}^{\mathrm{T}} \\\boldsymbol{\beta}^{\mathrm{T}} \\\boldsymbol{\gamma}^{\mathrm{T}}\end{array}\right)\left(2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}}+\boldsymbol{\beta} \boldsymbol{\beta}^{\mathrm{T}}\right)(\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}) \boldsymbol{y} \end{aligned} f ( x 1 , x 2 , x 3 ) = y T Q T ( 2 α α T + β β T ) Q y = y T α T β T γ T ( 2 α α T + β β T ) ( α , β , γ ) y = y T ( α T β T γ T ) ( 2 α , β , 0 ) y = y T ( 2 0 0 0 1 0 0 0 0 ) y \displaystyle \begin{aligned} =\boldsymbol{y}^{\mathrm{T}}\left(\begin{array}{l}\boldsymbol{\alpha}^{\mathrm{T}} \\\boldsymbol{\beta}^{\mathrm{T}} \\\boldsymbol{\gamma}^{\mathrm{T}}\end{array}\right)(2 \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{0}) \boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}}\left(\begin{array}{lll}2 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 0\end{array}\right) \boldsymbol{y} \end{aligned} = y T α T β T γ T ( 2 α , β , 0 ) y = y T 2 0 0 0 1 0 0 0 0 y = 2 y 1 2 + y 2 2 , \displaystyle \begin{aligned} =2 y_1^2+y_2^2, \end{aligned} = 2 y 1 2 + y 2 2 , f f f x = Q y x=Q y x = Q y 2 y 1 2 + y 2 2 2 y_1^2+y_2^2 2 y 1 2 + y 2 2 (22) 2024大概率不考,2023考过了
设随机变量 X X X f ( x ) = { 1 9 x 2 , 0 < x < 3 , 0 , 其他. \displaystyle f(x)=\left\{\begin{array}{ll}\frac{1}{9} x^{2}, & 0<x<3, \\ 0, & \text { 其他. }\end{array}\right. f ( x ) = { 9 1 x 2 , 0 , 0 < x < 3 , 其他 . Y = { 2 , X ⩽ 1 , X , 1 < X < 2 , 1 , X ⩾ 2. \displaystyle Y= \begin{cases}2, & X \leqslant 1, \\ X, & 1<X<2, \\ 1, & X \geqslant 2 .\end{cases} Y = ⎩ ⎨ ⎧ 2 , X , 1 , X ⩽ 1 , 1 < X < 2 , X ⩾ 2. Y Y Y P { X ⩽ Y } P\{X \leqslant Y\} P { X ⩽ Y }
(22) 通过这个二叉树结构,我们清晰地展示了求 Y Y Y P { X ⩽ Y } P\{X \leqslant Y\} P { X ⩽ Y } X X X Y Y Y Y Y Y
(I) 由题设知, P { 1 ⩽ Y ⩽ 2 } = 1 P\{1 \leqslant Y \leqslant 2\}=1 P { 1 ⩽ Y ⩽ 2 } = 1 Y Y Y F Y ( y ) F_Y(y) F Y ( y ) y < 1 y<1 y < 1 F Y ( y ) = 0 F_Y(y)=0 F Y ( y ) = 0 y ⩾ 2 y \geqslant 2 y ⩾ 2 F Y ( y ) = 1 F_Y(y)=1 F Y ( y ) = 1 1 ⩽ y < 2 1 \leqslant y<2 1 ⩽ y < 2 F Y ( y ) = P { Y ⩽ y } = P { Y = 1 } + P { 1 < Y ⩽ y } \displaystyle \begin{aligned} F_Y(y) & =P\{Y \leqslant y\}=P\{Y=1\}+P\{1<Y \leqslant y\} \end{aligned} F Y ( y ) = P { Y ⩽ y } = P { Y = 1 } + P { 1 < Y ⩽ y }
= P { X ⩾ 2 } + P { 1 < X ⩽ y } = ∫ 2 3 x 2 9 d x + ∫ 1 y x 2 9 d x = y 3 + 18 27 . \displaystyle \begin{aligned} =P\{X \geqslant 2\}+P\{1<X \leqslant y\}=\int_2^3 \frac{x^2}{9} \mathrm{~d} x+\int_1^y \frac{x^2}{9} \mathrm{~d} x=\frac{y^3+18}{27} . \end{aligned} = P { X ⩾ 2 } + P { 1 < X ⩽ y } = ∫ 2 3 9 x 2 d x + ∫ 1 y 9 x 2 d x = 27 y 3 + 18 . Y Y Y F Y ( y ) = { 0 , y < 1 , y 3 + 18 27 , 1 ⩽ y < 2 , 1 , y ⩾ 2. \displaystyle F_Y(y)= \begin{cases}0, & y<1, \\ \frac{y^3+18}{27}, & 1 \leqslant y<2, \\ 1, & y \geqslant 2 .\end{cases} F Y ( y ) = ⎩ ⎨ ⎧ 0 , 27 y 3 + 18 , 1 , y < 1 , 1 ⩽ y < 2 , y ⩾ 2. P { X ⩽ Y } = P { X < 2 } = ∫ 0 2 x 2 9 d x = 8 27 \displaystyle P\{X \leqslant Y\}=P\{X<2\}=\int_0^2 \frac{x^2}{9} \mathrm{~d} x=\frac{8}{27} P { X ⩽ Y } = P { X < 2 } = ∫ 0 2 9 x 2 d x = 27 8 P { Y ⩽ y } P\{Y \leqslant y\} P { Y ⩽ y } { Y ⩽ y } \{Y \leqslant y\} { Y ⩽ y } X X X 1 ⩽ y < 2 1 \leqslant y<2 1 ⩽ y < 2 F Y ( y ) = P { Y ⩽ y } = P { X ⩽ y } = ∫ 1 y x 2 9 d x = y 3 − 1 27 , \displaystyle F_Y(y)=P\{Y \leqslant y\}=P\{X \leqslant y\}=\int_1^y \frac{x^2}{9} \mathrm{~d} x=\frac{y^3-1}{27}, F Y ( y ) = P { Y ⩽ y } = P { X ⩽ y } = ∫ 1 y 9 x 2 d x = 27 y 3 − 1 , { Y ⩽ y } \{Y \leqslant y\} { Y ⩽ y } X X X F Y ( y ) F_Y(y) F Y ( y ) F Y ( y ) = P { Y ⩽ y } F_Y(y)=P\{Y \leqslant y\} F Y ( y ) = P { Y ⩽ y } F Y ( y ) F_Y(y) F Y ( y ) y = 1 y=1 y = 1 y = 2 y=2 y = 2 { X ⩽ Y } \{X \leqslant Y\} { X ⩽ Y } X X X { X < 2 } \{X<2\} { X < 2 } (23) (本题满分 11 分)
设总体 X X X f ( x ; θ ) = { θ 2 x 3 e − θ x , x > 0 , 0 , 其他, \displaystyle f(x ; \theta)=\left\{\begin{array}{ll}\frac{\theta^{2}}{x^{3}} \mathrm{e}^{-\frac{\theta}{x}}, & x>0, \\ 0, & \text { 其他, }\end{array}\right. f ( x ; θ ) = { x 3 θ 2 e − x θ , 0 , x > 0 , 其他 , θ \theta θ X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n X X X
(I) 求 θ \theta θ θ \theta θ
(23) 解 ( I ) 求矩估计就是求期望:求谁的期望,就在谁的前面乘x进行积分 求样本均值=也就是求总体期望 E X = ∫ − ∞ + ∞ x f ( x ) d x = 只有在 0 到 ∞ 有密度 ∫ 0 + ∞ x ⋅ θ 2 x 3 e − θ x d x \displaystyle E X=\int_{-\infty}^{+\infty} x f(x) d x\xlongequal[]{\text{只有在}0\text{到}\infty\text{有密度}}\int_0^{+\infty} x \cdot \frac{\theta^2}{x^3} \mathrm{e}^{-\frac{\theta}{x}} \mathrm{~d} x EX = ∫ − ∞ + ∞ x f ( x ) d x 只有在 0 到 ∞ 有密度 ∫ 0 + ∞ x ⋅ x 3 θ 2 e − x θ d x = 凑 ( − θ x ) ′ = θ ⋅ 1 x 2 ∫ 0 + ∞ θ e − θ x d ( − θ x ) = 换限 t = − θ x ∫ − ∞ 0 θ e t d t = θ e t ∣ − ∞ 0 = θ ⋅ e 0 − θ ⋅ 0 θ \displaystyle \xlongequal[]{\text{凑}\left(-\frac{\theta}{x}\right)^{\prime}=\theta \cdot \frac{1}{x^2}}\int_0^{+\infty} \theta \mathrm{e}^{-\frac{\theta}{x}} \mathrm{~d}\left(-\frac{\theta}{x}\right)\xlongequal[\text{换限}]{t=-\frac{\theta}{x}}\int_{-\infty}^0 \theta \mathrm{e}^t \mathrm{~d} t=\left.\theta \mathrm{e}^t\right|_{-\infty} ^0\xlongequal[]{\theta \cdot e^0-\theta \cdot 0}\theta 凑 ( − x θ ) ′ = θ ⋅ x 2 1 ∫ 0 + ∞ θ e − x θ d ( − x θ ) t = − x θ 换限 ∫ − ∞ 0 θ e t d t = θ e t − ∞ 0 θ ⋅ e 0 − θ ⋅ 0 θ 所以 θ \theta θ θ ^ = E ( X ) = 总体期望与样本均值 X ˉ \hat{\theta}=E(X)\xlongequal[]{\text{总体期望与样本均值}}\bar{X} θ ^ = E ( X ) 总体期望与样本均值 X ˉ X ˉ = 1 n ∑ i = 1 n X i \displaystyle \bar{X}=\frac{1}{n} \sum_{i=1}^n X_i X ˉ = n 1 i = 1 ∑ n X i 设 x 1 , x 2 , ⋯ , x n x_{1}, x_{2}, \cdots, x_{n} x 1 , x 2 , ⋯ , x n 写出似然函数:L ( θ ) = ∏ i = 1 n f ( x ; θ ) = { θ 2 n . 1 x 1 3 x 2 3 ⋯ x n 3 . e − θ ∑ i = 1 n 1 x i ⏟ 三项相乘 x 1 , x 2 , ⋯ x n > 0. 0 , 其他 \displaystyle L(\theta)=\prod_{i=1}^{n} f(x ; \theta)=\left\{\begin{array}{cc}\underbrace{{\theta^{2 n}}.\frac1{x_{1} ^3x_{2}^3 \cdots x_{n}^3}. e^{-\theta \sum_{i=1}^{n} \frac{1}{x_{i}}}}_{\text{三项相乘}} & x_{1}, x_{2}, \cdots x_{n}>0 . \\ 0, & \text { 其他 }\end{array}\right. L ( θ ) = i = 1 ∏ n f ( x ; θ ) = ⎩ ⎨ ⎧ 三项相乘 θ 2 n . x 1 3 x 2 3 ⋯ x n 3 1 . e − θ ∑ i = 1 n x i 1 0 , x 1 , x 2 , ⋯ x n > 0. 其他 取对数:ln L ( θ ) = ln θ 2 n + ln 1 x 1 3 ⋯ x n 3 ⏟ 常数求导为 0 − θ ∑ i = 1 n 1 x i \displaystyle \ln L(\theta)=\ln \theta^{2 n}+\underbrace{\ln \frac{1}{x_1^3 \cdots x_n^3}}_{\text{常数求导为}0}-\theta \sum_{i=1}^n \frac{1}{x_i} ln L ( θ ) = ln θ 2 n + 常数求导为 0 ln x 1 3 ⋯ x n 3 1 − θ i = 1 ∑ n x i 1 为什么取对数? 乘法变成加法 指数变成系数 容易求导:ln x = 1 x \ln x=\frac1x ln x = x 1 求导求驻点:令 d ln L ( θ ) d θ = 2 n θ − ∑ i = 1 n 1 x i = 0 \displaystyle \frac{d \ln L(\theta)}{d \theta}=\frac{2 n}{\theta}-\sum_{i=1}^{n} \frac{1}{x_{i}}=0 d θ d ln L ( θ ) = θ 2 n − i = 1 ∑ n x i 1 = 0 2 n θ = ∑ i = 1 n 1 x i → 移项 θ = 2 n ∑ i = 1 n 1 x i \displaystyle \frac{2 n}{\theta}=\sum_{i=1}^n \frac{1}{x_i}\xrightarrow[]{\text{移项}}\theta=\frac{2 n}{\sum_{i=1}^n \frac{1}{x_i}} θ 2 n = i = 1 ∑ n x i 1 移项 θ = ∑ i = 1 n x i 1 2 n 得 θ \theta θ 最大似然估计值 为 θ ^ = 2 n ∑ i = 1 n 1 x i \displaystyle \hat{\theta}= \frac{2n}{\sum_{i=1}^{n} \frac{1}{x_{i}}} θ ^ = ∑ i = 1 n x i 1 2 n 得 θ \theta θ 最大似然估计量 为 θ ^ = 2 n ∑ i = 1 n 1 X i \displaystyle \hat{\theta}= \frac{2n}{\sum_{i=1}^{n} \frac{1}{X_{i}}} θ ^ = ∑ i = 1 n X i 1 2 n 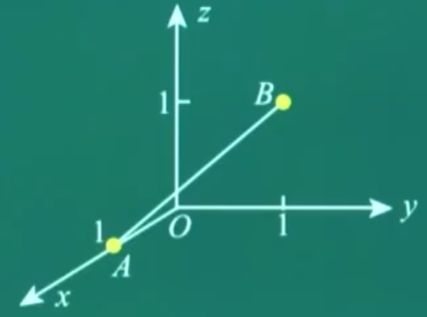 ,AB绕z轴旋转一周
,AB绕z轴旋转一周