一、选择题

(本题共 10 小题, 每小题 5 分, 共 50 分. 在每小题给出的四个选项中, 只有一项符合题目 要求,把所选项前的字母填在题后的括号内.

(1)

数一2022
设 $\displaystyle \lim _{x \rightarrow 1} \frac{f(x)}{\ln x}=1$, 则 $(\quad)$
(A) $f(1)=0$.
(B) $\displaystyle \lim _{x \rightarrow 1} f(x)=0$.
$(\mathrm{C}) f^{\prime}(1)=1$.
(D) $\displaystyle \lim _{x \rightarrow 1} f^{\prime}(x)=1$.
数一2022
答 应选 B.
解 $\displaystyle \lim _{x \rightarrow 1} \frac{f(x)}{\ln x}=1 \xrightarrow[]{\frac00} \lim _{x \rightarrow 1} f(x)=0$, 故选 B.

这道题的核心是理解给定的极限表达式和如何从中推断函数$f(x)$在$x \rightarrow 1$时的行为。下面是对答案的逐步解释：

• (1) 分析题式
  • 由原式 $\displaystyle \lim _{x \rightarrow 1} \frac{f(x)}{\ln x}=1$, 将 $x=1$ 代入分母，$\displaystyle \lim _{x \rightarrow 1} \ln x=0$
• (2)分子与分母为等价无穷小
  • 已知分母为0
  • 则分子也为 0 ，所以 $\displaystyle \lim _{x \rightarrow 1} f(x)=0$

(2)

数一2022
设 $f(u)$ 可导, $z=x y f\left(\frac{y}{x}\right)$, 若 $x \frac{\partial z}{\partial x}+y \frac{\partial z}{\partial y}=y^{2}(\ln y-\ln x)$, 则 ( )
(A) $f(1)=\frac{1}{2}, f^{\prime}(1)=0$.
(B) $f(1)=0, f^{\prime}(1)=\frac{1}{2}$.
(C) $f(1)=\frac{1}{2}, f^{\prime}(1)=1$.
(D) $f(1)=0, f^{\prime}(1)=1$.

(2)

• 乘法求导:先一后二
  
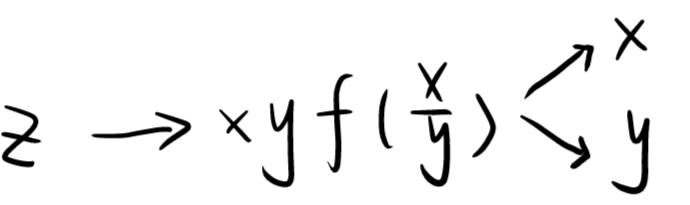
• 计算偏导数：
  • 计算 $z$ 对 $x$ 的偏导数：$\frac{\partial z}{\partial x} = yf\left(\frac{y}{x}\right) - y^2f'\left(\frac{y}{x}\right)\frac{1}{x}$
  • 计算 $z$ 对 $y$ 的偏导数：$\frac{\partial z}{\partial y} = xf\left(\frac{y}{x}\right) + xyf'\left(\frac{y}{x}\right)\frac{1}{x}$
• 将两个偏导数代入题式：$x\frac{\partial z}{\partial x} + y\frac{\partial z}{\partial y} = y^2(\ln y - \ln x)$
  • 得$xyf\left(\frac{y}{x}\right) - y^2f'\left(\frac{y}{x}\right) + xyf\left(\frac{y}{x}\right) + y^2f'\left(\frac{y}{x}\right) = y^2(\ln y - \ln x)$
  • 化简左边后，得：$2xyf\left(\frac{y}{x}\right) = y^2(\ln y - \ln x)$
    • $\xrightarrow[]{同除x^2}\frac yxf\left(\frac yx\right)=\left(\frac yx\right)^2\ln\frac yx.$
    • 令$\xrightarrow[]{u=\frac{y}{x}}u f(u)=u^2 \ln u$
      • 解出 : $f(u)=\frac{1}{2} u \ln u, u>0$.
• 第三步 : 计算 $f(1)$ 和 $f^{\prime}(1)$
  • $f(u)=\frac{1}{2} u \ln u\xlongequal[]{u=\frac{y}{x}=1}\frac12\cdot1\cdot\ln1=0$,
  • $f^{\prime}(u)\xlongequal[]{乘法求导}\frac12\left(\ln u+u\cdot\frac1u\right)=\frac12\left(\ln1+1\right)=\frac12$
• 因此, $f(1)=0, f^{\prime}(1)=\frac{1}{2}$.

(3)

数一2022
设数列 $\left\{x_{n}\right\}$ 满足 $-\frac{\pi}{2} \leqslant x_{n} \leqslant \frac{\pi}{2}$, 则 $(\quad)$
(A) 若 $\displaystyle \lim _{n \rightarrow \infty} \cos \left(\sin x_{n}\right)$ 存在, 则 $\displaystyle \lim _{n \rightarrow \infty} x_{n}$ 存在.
(B) 若 $\displaystyle \lim _{n \rightarrow \infty} \sin \left(\cos x_{n}\right)$ 存在, 则 $\displaystyle \lim _{n \rightarrow \infty} x_{n}$ 存在.
(C) 若 $\displaystyle \lim _{n \rightarrow \infty} \cos \left(\sin x_{n}\right)$ 存在,则 $\displaystyle \lim _{n \rightarrow \infty} \sin x_{n}$ 存在,但 $\displaystyle \lim _{n \rightarrow \infty} x_{n}$ 不一定存在.
(D) 若 $\displaystyle \lim _{n \rightarrow \infty} \sin \left(\cos x_{n}\right)$ 存在, 则 $\displaystyle \lim _{n \rightarrow \infty} \cos x_{n}$ 存在, 但 $\displaystyle \lim _{n \rightarrow \infty} x_{n}$ 不一定存在.

数一2022

• AC都是问的$\displaystyle \begin{aligned} \underbrace{\lim_{n \to \infty} \cos(\sin x_n)}_{cos\xrightarrow[]{内层}sin\xrightarrow[]{内层}x_n}\end{aligned}$ ，BD都是问的$\displaystyle \begin{aligned} \underbrace{\lim_{n \to \infty} \sin(\cos x_n)}_{sin\xrightarrow[]{内层}cos\xrightarrow[]{内层}x_n}\end{aligned}$
• A:由于 $\displaystyle \begin{aligned} \cos x \end{aligned}$ 在 [-1,1] 上是偶函数，当 $\displaystyle \begin{aligned} \underbrace{\lim_{n \to \infty} \cos(\sin x_n)}_{cos\xrightarrow[]{内层}sin\xrightarrow[]{内层}x_n}\end{aligned}$ 存在时，$\displaystyle \begin{aligned} \lim_{n \to \infty} \sin x_n \end{aligned}$ 和 $\displaystyle \begin{aligned} \lim_{n \to \infty} x_n \end{aligned}$ 都未必存在。
  • 如 $\displaystyle \begin{aligned} x_n = \begin{cases} \frac{\pi}{2}, & n \text{为偶} \\ -\frac{\pi}{2}, & n \text{为奇} \end{cases} \end{aligned}$，(里面这玩意)
  • $\displaystyle \begin{aligned} \lim_{n \to \infty} x_n \end{aligned}$ 和 $\displaystyle \begin{aligned} \lim_{n \to \infty} \sin x_n \end{aligned}$ 都不存在，但 $\displaystyle \begin{aligned} \lim_{n \to \infty} \cos(\sin x_n) = \cos(\pm 1) = \cos 1 \end{aligned}$。
• D:由于 $\displaystyle \begin{aligned} \sin x \end{aligned}$ 在 [0,1] 上单调增，所以当 $\displaystyle \begin{aligned} \lim_{n \to \infty} \sin(\cos x_n) \end{aligned}$ 存在时，必有 $\displaystyle \begin{aligned} \lim_{n \to \infty} \cos x_n \end{aligned}$ 存在，
  • 又 $\displaystyle \begin{aligned} \cos x \end{aligned}$ 是偶函数，所以此时 $\displaystyle \begin{aligned} \lim_{n \to \infty} x_n \end{aligned}$ 未必存在。
• 总结:
  • 外层是偶函数，内层不一定存在
  • 外层是奇函数，并且在区间上单调，内层一定存在

(4)

数一2022
若 $\displaystyle I_{1}=\int_{0}^{1} \frac{x}{2(1+\cos x)} \mathrm{d} x, I_{2}=\int_{0}^{1} \frac{\ln (1+x)}{1+\cos x} \mathrm{~d} x, I_{3}=\int_{0}^{1} \frac{2 x}{1+\sin x} \mathrm{~d} x$, 则 ( )
(A) $I_{1}<I_{2}<I_{3}$.
(B) $I_{2}<I_{1}<I_{3}$.
(C) $I_{1}<I_{3}<I_{2}$.
(D) $I_{3}<I_{2}<I_{1}$.

让我们一步一步地解释这个积分比较问题的解答过程。

• 函数大，积分就大
  • 相同区间，只需要比较内部的被积函数
• 比较$\displaystyle \begin{aligned} I_1 和I_2 \end{aligned}$(常用不等式，比较分母)
  • 当 $\displaystyle \begin{aligned} x > 0 \end{aligned}$ 时，有常用不等式: $\displaystyle \begin{aligned} \frac{x}{1+x} < \ln(1+x) < x \end{aligned}$。
  • 特别是当 $\displaystyle \begin{aligned} x \in (0, 1) \end{aligned}$ 时，$\displaystyle \begin{aligned} \underbrace{\frac{x}{2} < \frac{x}{1+x}}_{1+x<2} < \ln(1+x) \end{aligned}$，故 $\displaystyle \begin{aligned} I_1 < I_2 \end{aligned}$。
• 比较$I_2 < I_3$(比较分母)
  • 另外当 $\displaystyle \begin{aligned} x \in (0, 1) \end{aligned}$ 时，$\displaystyle \begin{aligned} \frac{\ln(1+x)}{1+\cos x} < \frac{\ln(1+x)}{1} = \ln(1+x) \end{aligned}$
  • $\displaystyle \begin{aligned} \underbrace{\ln(1+x)}_{I_2<\ln(1+x)}< x < \underbrace{\frac{2}{1+\sin x} \cdot x}_{I_3}, \xrightarrow[]{只比较x的系数}1 < \underbrace{\frac{2}{1+\sin x}}_{1+\sin x<2}, \text{故} I_2 < I_3. \end{aligned}$

(5)

数一2022

• 下列 4 个条件中, 3 阶矩阵 $\boldsymbol{A}$ 可相似对角化的一个充分非必要条件是 ( )
  (A) $\boldsymbol{A}$ 有 3 个不同的特征值.
  (B) $A$ 有 3 个线性无关的特征向量.
  (C) $\boldsymbol{A}$ 有 3 个两两线性无关的特征向量.
  (D) $\boldsymbol{A}$ 的属于不同特征值的特征向量相互正交.

数一2022

• A:由题意，3个不同特征值可以推出 $\displaystyle \begin{aligned} A \end{aligned}$ 能相似对角化，但是反之不能推出，故选 $\displaystyle \begin{aligned} A \end{aligned}$。
  • A能相似对角化，但A不一定有三个不同的特征值。
  • 如果A有二重根，并且二重根有两个特征向量，则A也可以相似对角化
• B:其中 $\displaystyle \begin{aligned} (B) \end{aligned}$ 是充分必要条件。
• C:其中 $\displaystyle \begin{aligned} (C) \end{aligned}$ 是必要非充分条件，
  • 证充分性:因为有3个两两无关的特征向量，则这3个特征向量可能相关，
    比如 $\displaystyle \begin{aligned} \alpha_1 = [1, 0, 0]^T, \alpha_2 = [0, 1, 0]^T, \alpha_3 = [1, 1, 0]^T \end{aligned}$。
  • 证必要性:而当3个特征向量无关时，这3个特征向量必两两无关。
• D:其中 $\displaystyle \begin{aligned} (D) \end{aligned}$ 不意味着 $\displaystyle \begin{aligned} A \end{aligned}$（3阶矩阵）有3个相互正交的特征向量，
  • 比如，$\displaystyle \begin{aligned} \lambda_1 = \lambda_2 = 1 \end{aligned}$，但该二重特征值可能只有一个无关特征向量 $\displaystyle \begin{aligned} \xi_1 \end{aligned}$，
  • 而 $\displaystyle \begin{aligned} \lambda_3 = 0 \end{aligned}$，该单根有（且只有）一个无关的特征向量 $\displaystyle \begin{aligned} \xi_2 \end{aligned}$，
  • 此时完全可以有 $\displaystyle \begin{aligned} \xi_1 \end{aligned}$ 与 $\displaystyle \begin{aligned} \xi_2 \end{aligned}$ 正交这种情形，但是二重根只有一个特征向量，所以不能相似对角化

(6)

数一2022

• 设 $\boldsymbol{A}, \boldsymbol{B}$ 为 $n$ 阶矩阵, $\boldsymbol{E}$ 为 $n$ 阶单位矩阵,若$\underbrace{方程组 \boldsymbol{A x}=\mathbf{0} 与 \boldsymbol{B} \boldsymbol{x}=\mathbf{0} 同解}_{同零解还是非零解}$, 则 ( )
  (A) $\displaystyle \left(\begin{array}{ll}\boldsymbol{A} & \boldsymbol{O} \\ \boldsymbol{E} & B\end{array}\right) \boldsymbol{y}=\mathbf{0}$ 只有零解.
  (B) $\displaystyle \left(\begin{array}{cc}\boldsymbol{E} & \boldsymbol{A} \\ \boldsymbol{O} & \boldsymbol{A B}\end{array}\right) \boldsymbol{y}=\mathbf{0}$ 只有零解. (C) $\displaystyle \left(\begin{array}{ll}A & B \\ O & B\end{array}\right) y=0$ 与 $\displaystyle \left(\begin{array}{cc}B & A \\ O & A\end{array}\right) y=0$ 同解.
  (D) $\displaystyle \left(\begin{array}{cc}A B & B \\ O & A\end{array}\right) y=0$ 与 $\displaystyle \left(\begin{array}{cc}B A & A \\ O & B\end{array}\right) y=0$ 同解.

数一2022
答 应选 C.

• 对 $\displaystyle (A),\left|\begin{array}{cc}{A} & O \\ E & B\end{array}\right|\xlongequal[]{拉普拉斯}|A| \cdot|B|$ 是否为 0 不确定。
• 对 $\displaystyle \begin{aligned} (B) \end{aligned}$，$\displaystyle \begin{aligned} \left|\begin{array}{cc}E & A \\ O & AB\end{array}\right| = |E| \cdot |AB| = |A| \cdot |B| \end{aligned}$ 是否为 0 不确定。
• 对 $\displaystyle \begin{aligned} (C) \end{aligned}$，$\displaystyle \begin{aligned} \left[\begin{array}{cc}A & B \\ O & B\end{array}\right] \xrightarrow[]{c1-c2} \left[\begin{array}{cc}A & O \\ O & B\end{array}\right], \quad \left[\begin{array}{cc}B & A \\ O & A\end{array}\right] \xrightarrow[]{c1-c2} \left[\begin{array}{cc}B & O \\ O & A\end{array}\right] \end{aligned}$
  • 因为 $\displaystyle \begin{aligned} Ax = 0 \end{aligned}$ 与 $\displaystyle \begin{aligned} Bx = 0 \end{aligned}$ 同解，
    注意行变换是同解的，列变换是不同解的
    • 于是 $\displaystyle \begin{aligned} \left[\begin{array}{cc} A & O \\ O & B\end{array}\right] x = 0 \end{aligned}$ 与 $\displaystyle \begin{aligned} \left[\begin{array}{cc} B & O \\ O & A\end{array}\right] x = 0 \end{aligned}$ 也同解。
    • 进而 $\displaystyle \begin{aligned} \left[\begin{array}{cc} A & B \\ O & B\end{array}\right] y = 0 \end{aligned}$ 与 $\displaystyle \begin{aligned} \left[\begin{array}{cc} B & A \\ O & A\end{array}\right] y = 0 \end{aligned}$ 同解。
    • 实际上，$\displaystyle \begin{aligned} \left[\begin{array}{cc}A & AB \\ O & B\end{array}\right] x = 0 \end{aligned}$，和 $\displaystyle \begin{aligned} \left[\begin{array}{cc} B & BA \\ O & A\end{array}\right] x = 0 \end{aligned}$ 也同解
• D选项是列变换，错误

(7)

数一2022
设 $\boldsymbol{\alpha}_{1}=(\lambda, 1,1)^{\mathrm{T}}, \boldsymbol{\alpha}_{2}=(1, \lambda, 1)^{\mathrm{T}}, \boldsymbol{\alpha}_{3}=(1,1, \lambda)^{\mathrm{T}}, \boldsymbol{\alpha}_{4}=\left(1, \lambda, \lambda^{2}\right)^{\mathrm{T}}$, 若 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}$ 与 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}$, $\boldsymbol{\alpha}_{4}$ 等价,则 $\lambda$ 的取值范围是 $(\quad)$
(A) $\{0,1\}$.
(B) $\{\lambda \mid \lambda \in \mathbf{R}, \lambda \neq-2\}$.
(C) $\{\lambda \mid \lambda \in \mathbf{R}, \lambda \neq-1, \lambda \neq-2\}$.
(D) $\{\lambda \mid \lambda \in \mathbf{R}, \lambda \neq-1\}$.

• 解：因为 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 与 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 等价，所以 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 与 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 可相互表示。
  • $\displaystyle \begin{aligned} \alpha_3 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 表示。
  • $\displaystyle \begin{aligned} \alpha_4 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3\end{aligned}$ 表示。
• 若 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 表示，则 $\displaystyle \begin{aligned} \alpha_3 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$表示。
  • 即非齐次方程组 $\displaystyle \begin{aligned} x_1\alpha_1 + x_2\alpha_2 + x_3\alpha_4 = \alpha_3 \end{aligned}$ 有解。
  • 考虑 $\displaystyle \begin{aligned} \left|\alpha_1, \alpha_2, \alpha_4\right| = \left|\begin{array}{ccc} \lambda & 1 & 1 \\ 1 & \lambda & \lambda \\ 1 & 1 & \lambda^2 \end{array}\right| = (\lambda^2 - 1)^2 \end{aligned}$，行列式不等于0
    • 当 $\displaystyle \begin{aligned} \lambda \neq \pm 1 \end{aligned}$ 时，$\displaystyle \begin{aligned} \alpha_3 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 表示。
      • 当 $\displaystyle \begin{aligned} \lambda = 1 \end{aligned}$ 时，$\displaystyle \begin{aligned} \alpha_1 = \alpha_2 = \alpha_3 = \alpha_4 = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \end{aligned}$，显然 $\displaystyle \begin{aligned} \alpha_3 \end{aligned}$ 仍可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 表示。
      • 当 $\displaystyle \begin{aligned} \lambda = -1 \end{aligned}$ 时，$\displaystyle \begin{aligned} (\alpha_1, \alpha_2, \alpha_4 | \alpha_3) \rightarrow \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned}$，此时 $\displaystyle \begin{aligned} \alpha_3 \end{aligned}$ 不可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 表示。
  • 得出 $\displaystyle \begin{aligned} \lambda = -1 \end{aligned}$
• 若 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_4 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 表示，则 $\displaystyle \begin{aligned} \alpha_4 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 表示。
  即非齐次方程组 $\displaystyle \begin{aligned} x_1\alpha_1 + x_2\alpha_2 + x_3\alpha_3 = \alpha_4 \end{aligned}$ 有解。
  • 考虑 $\displaystyle \begin{aligned} \left|\alpha_1, \alpha_2, \alpha_3\right| = \left|\begin{array}{ccc} \lambda & 1 & 1 \\ 1 & \lambda & 1 \\ 1 & 1 & \lambda \end{array}\right| = (\lambda + 2)(\lambda - 1)^2 \end{aligned}$，行列式不为0
    • 行列式如果为零，则线性无关
  • 当 $\displaystyle \begin{aligned} \lambda \neq -2 \end{aligned}$ 且 $\displaystyle \begin{aligned} \lambda \neq 1 \end{aligned}$ 时，$\displaystyle \begin{aligned} \alpha_4 \end{aligned}$ 可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 表示。
    • 当 $\displaystyle \begin{aligned} \lambda = 1 \end{aligned}$ 时，$\displaystyle \begin{aligned} \alpha_1 = \alpha_2 = \alpha_3 = \alpha_4 = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \end{aligned}$，显然 $\displaystyle \begin{aligned} \alpha_4 \end{aligned}$ 仍可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 表示。
    • 当 $\displaystyle \begin{aligned} \lambda = -2 \end{aligned}$ 时，$\displaystyle \begin{aligned} \left(\alpha_1, \alpha_2, \alpha_3 \mid \alpha_4\right) \rightarrow \begin{pmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}, \end{aligned}$此时 $\displaystyle \begin{aligned} \alpha_4 \end{aligned}$ 不可由 $\displaystyle \begin{aligned} \alpha_1, \alpha_2, \alpha_3 \end{aligned}$ 表示。
  • 得出 $\displaystyle \begin{aligned} \lambda = -2 \end{aligned}$
• 故 $\displaystyle \begin{aligned} \lambda \end{aligned}$ 的取值范围为 $\displaystyle \begin{aligned} \{\lambda \mid \lambda \in \mathbb{R}, \lambda \neq -1, \lambda \neq -2\} \end{aligned}$，故选 C

(8)

数一2022
设随机变量 $X$ 服从区间 $(0,3)$ 上的均匀分布, 随机变量 $Y$ 服从参数为 2 的泊松分布, 且 $X$ 与 $Y$ 的协方差为 -1 , 则 $D(2 X-Y+1)=(\quad)$
(A) 1 .
(B) 5 .
(C) 9 .
(D) 12 .

(8)

• 方法一：$\displaystyle \begin{aligned} D(2X - Y + 1) = 4DX + DY - 2Cov(2X, Y) \end{aligned}$

  • $\displaystyle \begin{aligned} \xlongequal[]{提出系数} 4DX + DY - 2 \cdot 2Cov(X, Y) \end{aligned}$
  • $\displaystyle \begin{aligned} \xlongequal[D(Y)=λ]{D(X)=\frac{(a-b)^2}{12} } 4 \cdot \frac{3^2}{12} + 2 - 2 \cdot 2 \cdot (-1) = 9 \end{aligned}$

• 方法二：

  • 应用方差的性质
    • 方差的一个重要性质是 $D(aX + bY + c) = a^2DX + b^2DY + 2ab \, \text{Cov}(X, Y)$
      • 其中 $a, b, c$ 是常数
      • $\text{Cov}(X, Y)$ 是 $X$ 和 $Y$ 的协方差。
    • 应用这个性质，对于 $D(2X - Y + 1)$ 有：
      $D(2X - Y + 1) = 4DX + DY - 4 \text{Cov}(X, Y)$
  • 第一步：计算 $X$ 和 $Y$ 的方差
    • 对于均匀分布的随机变量 $X$，其方差 $DX$ 可以用公式 $DX = \frac{(b-a)^2}{12}$ 计算，其中 $a$ 和 $b$ 是区间的下限和上限。因此，对于 $X$ 有：$DX = \frac{(3-0)^2}{12} = \frac{3}{4}$
    • 对于参数为 2 的泊松分布的随机变量 $Y$，其方差 $DY$ 等于其参数，即 $DY = 2$。
  • 将 $DX, DY, \text{Cov}(X, Y)=-1$ 的值代入到最初的式子，得到：$D(2X - Y + 1) =4DX + DY - 4 \text{Cov}(X, Y) 4 \times \frac{3}{4} + 2 - 4 \times (-1) = 3 + 2 + 4 = 9$

(9)

数一2022

• 设随机变量 $X_{1}, X_{2}, \cdots, X_{n}$ 独立同分布, 且 $X_{1}$ 的 4 阶矩存在, $\underbrace{E\left(X_{1}^{k}\right)=\mu_{k}(k=1,2,3,4)}_{重点}$, 则根据 切比雪夫不等式, 对任意 $\varepsilon>0$, 都有 $\displaystyle P\left\{\left|\frac{1}{n} \sum_{i=1}^{n} X_{i}^{2}-\mu_{2}\right| \geqslant \varepsilon\right\} \leqslant(\quad)$
  (A) $\frac{\mu_{4}-\mu_{2}^{2}}{n \varepsilon^{2}}$.
  (B) $\frac{\mu_{4}-\mu_{2}^{2}}{\sqrt{n} \varepsilon^{2}}$.
  (C) $\frac{\mu_{2}-\mu_{1}^{2}}{n \varepsilon^{2}}$.
  (D) $\frac{\mu_{2}-\mu_{1}^{2}}{\sqrt{n} \varepsilon^{2}}$.

• • 切比雪夫不等式:需要分别求期望和方差
    • 设随机变量 $X$ 具有数学期望 $E(X)=\mu$, 方差 $\displaystyle D(X)=\sigma^2$,
      • 则对于任意正数 $\varepsilon$, 不等式$\displaystyle \begin{aligned} P\{|X-\mu| \geq \varepsilon\} \leq \frac{\sigma^2}{\varepsilon^2} \end{aligned}$成立.

• 公式 $D(X)=E\left(X^2\right)-[E(X)]^2$.

  • $\displaystyle \begin{aligned} E\left(\frac{1}{n}\sum_{i=1}^n X_i^2\right) \xlongequal[]{提系数} \frac{1}{n} E\left(\sum_{i=1}^n X_i^2\right) \xlongequal[]{独立同分布}\frac{1}{n} \cdot n E\left(X_1^2\right) =\mu_2 \end{aligned}$
  • $\displaystyle \begin{aligned} D\left(\frac{1}{n}\sum_{i=1}^n X_i^2\right) \xlongequal[]{提系数} \left(\frac{1}{n}\right)^2 D\left(\sum_{i=1}^n X_i^2\right) \xlongequal[]{独立，则不考虑协方差}\left(\frac{1}{n}\right)^2 \cdot n D\left(X_1^2\right) \end{aligned}$
    • $\displaystyle \begin{aligned} \xlongequal[]{平方的期望减期望的平方} \left(\frac{1}{n}\right)^2 \cdot n \left\{ \underbrace{E\left[\left(X_1^2\right)^2\right]}_{\mu_4} - \underbrace{\left[E\left(X_1^2\right)\right]^2}_{\mu_2} \right\}=\frac{1}{n}\left(\mu_4-\mu_2^2\right) \end{aligned}$

• 故 $\displaystyle \begin{aligned} P\left\{ \left| \frac{1}{n} \sum_{i=1}^{n} X_i^2 - \mu_2 \right| \geq \varepsilon \right\} \leq \frac{D\left( \frac{1}{n} \sum_{i=1}^{n} X_i^2 \right)}{\varepsilon^2} = \frac{\mu_4 - \mu_2^2}{n\varepsilon^2} \end{aligned}$。故选 A。

• 设随机变量 $X$ 的数学期望 $E(X)=\mu$, 方差 $\displaystyle D(X)=\sigma^2$, 则由切比雪夫不等式, 有 $\displaystyle P\{|X-\mu| \geq 3 \sigma\} \leq$ $\qquad$ (1989 年数学三试题)

• 设随机变量 $X$ 的方差为 2 ，则根据切比雪夫不等式有估计 $P\{|X-E(X)| \geq 2\} \leq$ $\qquad$。(2001 年数学一试题)

• 设随机变量 $X$ 和 $Y$ 的数学期望分别为 -2 和 2 , 方差分别为 1和 4 , 而相关系数为 -0.5 , 则根据切比雪夫不等式 $P\{|X+Y| \geq 6\} \leq$.(2001 年数学三试题)

(10)

数一2022
设$\underbrace{随机变量 X \sim N(0,1)}_{X的边缘密度}$, $\underbrace{若在 X=x 的条件下, 随机变量 Y \sim N(x, 1)}_{Y的条件密度}$, 则 $X$ 与 $Y$ 的相关系数 为 $(\quad)$
(A) $\frac{1}{4}$.
(B) $\frac{1}{2}$.
(C) $\frac{\sqrt{3}}{3}$.
(D) $\frac{\sqrt{2}}{2}$.

• 25张宇八套卷#8-1#10
• 亚当夏娃
  • 亚当公式:$\displaystyle E Y=E(\underbrace{E(Y \mid x)}_{指数分布X})=E X=\int_{-\infty}^{+\infty} x f(x) d x$
  • 夏娃公式:$D Y=E(D(Y \mid x))+D(E(Y \mid X))$
  • $E(X Y)=E[E(X Y \mid X)]=E[X \underbrace{E(Y \mid X)}_{N(X,1)}]$
• 正态分布$\displaystyle N\left(\mu, \sigma^2\right)$，随机变量 $X \sim N(0,1)$
  • $E(X)=0$
  • $D(X)=1$
  • $E\left(X^2\right)=D(X)+[E(X)]^2=1+0=1$
• 若在 $X=x$ 的条件下, 随机变量 $Y \sim N(x, 1)$，由亚当夏娃公式
  • $\displaystyle \begin{aligned} E(Y)=E[E(Y \mid X)]=E(X)=0, \end{aligned}$
  • $\displaystyle \begin{aligned} D(Y)=E[\underbrace{D(Y \mid X)}_{1}]+D[\underbrace{E(Y \mid X)}_{X}]=E1+DX=1+1=2\end{aligned}$
  • $\displaystyle \begin{aligned} E(X Y)=E[E(X Y \mid X)]=E[X \underbrace{E(Y \mid X)}_{N(X,1)}]=E\left(X^2\right)=1\end{aligned}$
• $\displaystyle \begin{aligned}\rho_{X Y}=\frac{\operatorname{Cov}(x, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{1-0 \cdot 0}{\sqrt{2} \cdot \sqrt{1}}=\frac{\sqrt{2}}{2}\end{aligned}$
• 现在重点是求$E(XY)和D(Y)，E(Y)$

二、填空题

(本题共 6 小题, 每小题 5 分, 共 30 分, 把答案填在题中横线上.)

(11)

数一2022
函数 $f(x, y)=x^{2}+2 y^{2}$ 在点 $(0,1)$ 处的最大方向导数为

数一2022
答 应填 4.

• 定义
  • 方向导数描述了函数在某一点沿着特定方向的变化率。
  • 梯度 $\nabla f$ 是一个向量，其方向是函数增长最快的方向，其模是该点的最大方向导数。
• 解 沿着梯度方向, 方向导数最大, 最大值为梯度的模, 首先求梯度:
  • $\left.\frac{\partial f}{\partial x}\right|_{(0,1)}=\left.2 x\right|_{(0.1)}=0$
  • $\left.\frac{\partial f}{\partial y}\right|_{(0,1)}=\left.4 y\right|_{(0,1)}=4$
  • $\left.\operatorname{grad} f\right|_{(0.1)}=0 i+4 j .$
• 梯度的模是最大方向导数的值。
  • 故在点 $(0,1)$ 处最大的方向导数为 $|\operatorname{grad} f|_{(0,1)} \mid=\sqrt{0^2+4^2}=4$.

(12)

数一2022
$\displaystyle \int_{1}^{e^{2}} \frac{\ln x}{\sqrt{x}} \mathrm{~d} x=$
解

• 计算定积分 $\displaystyle \int_{1}^{e^{2}} \frac{\ln x}{\sqrt{x}} \mathrm{d} x$。

  • 使用分部积分法。
  • 选择 $u = \ln x$，则 $\mathrm{d}u = \frac{1}{x} \mathrm{d}x$。
  • 选择 $\mathrm{d}v = \frac{1}{\sqrt{x}} \mathrm{d}x$，则 $v = 2\sqrt{x}$。

• 应用分部积分公式 $\displaystyle \int u \, \mathrm{d}v = uv - \int v \, \mathrm{d}u$。

  • 得到 $\displaystyle \int_{1}^{e^{2}} \ln x \, \mathrm{d}(2\sqrt{x}) \xlongequal[]{分布} \left.2\sqrt{x} \ln x\right|_1^{e^{2}} - \int_{1}^{e^{2}} 2\sqrt{x} \cdot \frac{1}{x} \mathrm{d} x$。
    • 计算 $2\sqrt{x} \underbrace{\ln x|_1^{e^{2}}}_{lne^{2}-ln1} \xlongequal[]{ln1=0} 4e$。
    • 计算 $\displaystyle \int_{1}^{e^{2}} 2\sqrt{x} \cdot \frac{1}{x} \mathrm{d} x = 2 \cdot 2 \underbrace{\sqrt{x}|_1^{e^{2}}}_{\sqrt{e^{2}}-\sqrt{1^{2}}} = 4e - 4$。
  • 得 $4e - (4e - 4) = 4$。

综上，定积分 $\displaystyle \int_{1}^{e^{2}} \frac{\ln x}{\sqrt{x}} \mathrm{d} x = 4$。

(12)

数一2022
答 应填 4 .
解

• $\displaystyle \begin{aligned} \int_1^{e^2} \frac{\ln x}{\sqrt{x}} \mathrm{~d} x & =\int_1^{e^2} \ln x \mathrm{~d}(2 \sqrt{x})=\left.2 \sqrt{x} \cdot \ln x\right|_1 ^{e^2}-\int_1^{e^2} 2 \sqrt{x} \cdot \frac{1}{x} \mathrm{~d} x \end{aligned}$
• $\displaystyle \begin{aligned} =4 \mathrm{e}-2 \int_1^{e^2} \frac{1}{\sqrt{x}} \mathrm{~d} x=4 \mathrm{e}-\left.2 \cdot 2 \sqrt{x}\right|_1 ^{\mathrm{e}^{\prime}} \end{aligned}$
• $\displaystyle \begin{aligned} =4 \mathrm{e}-(4 \mathrm{e}-4)=4 . \end{aligned}$

这个题目是关于计算定积分 $\displaystyle \int_{1}^{e^{2}} \frac{\ln x}{\sqrt{x}} \, \mathrm{d} x$ 的。我们来逐步解析这个问题。

题目：
计算定积分 $\displaystyle \int_{1}^{e^{2}} \frac{\ln x}{\sqrt{x}} \, \mathrm{d} x$。

分步解释：

• 第一步：使用积分的换元法

  • 由于积分中包含 $\ln x$ 和 $\sqrt{x}$，可以考虑使用换元法。
  • 选择合适的换元，这里可以选择 $u = 2\sqrt{x}$，因此 $\mathrm{d}u = \frac{1}{\sqrt{x}} \mathrm{d}x$。

• 第二步：进行换元并计算新的积分

  • 将原积分转换为 $\displaystyle \int \ln x \, \mathrm{d}(2\sqrt{x})$。
  • 使用分部积分法，设 $u = \ln x$，$\mathrm{d}v = \mathrm{d}(2\sqrt{x})$。
  • 计算 $\mathrm{d}u = \frac{1}{x} \mathrm{d}x$ 和 $v = 2\sqrt{x}$。

• 第三步：应用分部积分公式

  • 分部积分公式为 $\displaystyle \int u \, \mathrm{d}v = uv - \int v \, \mathrm{d}u$。
  • 应用分部积分，得到 $\displaystyle \int_1^{e^2} \ln x \, \mathrm{d}(2\sqrt{x}) \xlongequal[]{分布} \left.2\sqrt{x} \ln x\right|_1^{e^2} - \int_1^{e^2} 2\sqrt{x} \cdot \frac{1}{x} \, \mathrm{d}x$。

• 第四步：计算并简化表达式

  • 计算 $\left.2\sqrt{x} \ln x\right|_1^{e^2} = 4e$。
  • 计算 $\displaystyle \int_1^{e^2} 2\sqrt{x} \cdot \frac{1}{x} \, \mathrm{d}x = \int_1^{e^2} \frac{2}{\sqrt{x}} \, \mathrm{d}x$。
  • 这个积分可以直接计算为 $\left.2 \cdot 2\sqrt{x}\right|_1^{e^2} = 4e - 4$。

• 第五步:将上述结果组合，得到 $4e - (4e - 4) = 4$。

(13)

数一2022
当 $x \geqslant 0, y \geqslant 0$ 时, $x^{2}+y^{2} \leqslant k \mathrm{e}^{x+y}$ 恒成立, 则 $k$ 的取值范围是

数一2022

• 转换不等式 $x^{2}+y^{2} \leqslant k \mathrm{e}^{x+y}$ 到新的形式。

• 引入新函数 $f(x, y) = \left(x^2+y^2\right) \mathrm{e}^{-x-y}$。

  • 目的是使不等式变为 $f(x, y) \leqslant k$。

• 求内部的驻点

  • 对求偏导
    • $f_x^{\prime}(x, y)=\frac{2 x \mathrm{e}^{x+y}-\mathrm{e}^{x+y}\left(x^2+y^2\right)}{\mathrm{e}^{2(x+y)}}$=$\underbrace{\left(2 x-x^2-y^2\right)}_{=0} \cdot \underbrace{e^{-(x+y)}}_{\neq 0}$
    • $f_y^{\prime}(x, y)=\frac{2 y \mathrm{e}^{x+y}-\mathrm{e}^{x+y}\left(x^2+y^2\right)}{\mathrm{e}^{2(x+y)}}$=$\underbrace{\left(2 y-x^2-y^2\right)}_{=0} \cdot \underbrace{e^{-(x+y)}}_{\neq 0}$
  • 令 $f_x^{\prime}(x, y)=0$，$f_y^{\prime}(x, y)=0$ 得
    • $\displaystyle \begin{aligned} 2 x-x^2-y^2=0 \\2 y-x^2-y^2=0 \end{aligned}$
      • 两式相减，得 $2 x-2 y=0 ，$ 则 $x=y$
      • 用消元法化简，$2 x-x^2-y^2=0\xrightarrow[]{x=y}2 x-2 x^2=0 ,分解 2 x(1-x)=0$，得$x=0, x=1$
  • 将 $x=0$ 代入式子，得两个驻点 $(0,0) ,( 1,1)$
    • $(0,0)$是边界上的点，故舍去
  • 则$f\left(1,1\right)=2\mathrm{e}^{-2}.$

• 求解 $f(x, y)$ 的最大值，分别考虑边界情况 $x = 0$ 和 $y = 0$。

• 当 $x = 0$ 时，求解 $f(0, y)=y^2\mathrm{e}^{-y}$ 的最大值

  • 通过求导 $f_y^{\prime}(0, y)=2y\mathrm{e}^{-y}-y^2\mathrm{e}^{-y}=0=(2y-y^{2})\cdot e^{-y}$ 并令其为 $0$
    • 找到可能的最大值点 $y = 0$ 和 $y = 2$。
    • 计算 $f(0, 0)$ 和 $f(0, 2)$，得到 $f(0, 2) = 4 \mathrm{e}^{-2}$。

• 当 $y = 0$ 时，求解 $f(x, 0)$ 的最大值。

  • 同样方法求导 $f_x^{\prime}(x, 0)$，找到最大值点 $x = 0$ 和 $x = 2$。
  • 计算 $f(0, 0)$ 和 $f(2, 0)$，得到 $f(2, 0) = 4 \mathrm{e}^{-2}$。

• 综合比较得到的值，确定 $f(x, y)$ 的最大值。

  • 通过比较，确定 $\max f(x, y) = 4 \mathrm{e}^{-2}$。

• 确定 $k$ 的取值范围。

  • 由于 $f(x, y) \leqslant k$，且 $\max f(x, y) = 4 \mathrm{e}^{-2}$，所以 $k \geqslant 4 \mathrm{e}^{-2}$。

因此，$k$ 的取值范围是 $\left[4 \mathrm{e}^{-2},+\infty\right)$

(14)

数一2022
已知级数 $\displaystyle \sum_{n=1}^{\infty} \frac{n !}{n^{n}} \mathrm{e}^{-n x}$ 的收敛域为 $(a,+\infty)$, 则 $a=$

1. 思路分析:

• 确定题目考查的是函数项级数收敛域的计算。

• 确定级数为正项级数，考虑使用比值审敛法

  • 若 $\displaystyle \lim _{n \rightarrow \infty} \frac{u_{n+1}}{u_n}=\rho\left\{\begin{array}{l}<1, \text { 级数 } \sum_{n=1}^{\infty} u_n \text { 收玫, } \\ >1, \text { 级数 } \sum_{n=1}^{\infty} u_n \text { 发散, } \\ =1, \text { 此判别法失效. }\end{array}\right.$

• 第一步: 使用比值审敛法。

• 定义 $u_n = \frac{n !}{n^n} e^{-nx}$，并求其极限。

  • 计算 $\displaystyle \lim_{n \to \infty} \frac{u_{n+1}}{u_n}$。
    • 求 $u_n$ 和 $u_{n+1}$ 表达式
      • $u_n=\frac{n!}{n^n}\mathrm{e}^{-nx}$
      • $u_{n+1}=\frac{(n+1)!}{{(n+1)}^{n+1}}\mathrm{e}^{-(n+1)x}$
      • 对系数化简$\displaystyle \begin{aligned} \frac{(n+1)!}{\left(n+1\right)^{n+1}}&=\frac{\left(n+1\right)n!}{\left(n+1\right)^{n+1}}=\frac{n!}{\left(n+1\right)^{n}}. \end{aligned}$

• 代入计算

  • $\displaystyle \lim_{n \to \infty} \frac{u_{n+1}}{u_n}$=$\displaystyle \lim_{n\to\infty}\frac{\frac{n!}{(n+1)^n}}{\frac{n!}{n^n}}\cdot\frac{\mathrm{e}^{-(n+1)x}}{\mathrm{e}^{-nx}}$
    =$\displaystyle \lim _{n \rightarrow \infty} \frac{n !}{(n+1)^n} \cdot \frac{n^n}{n !} \cdot \frac{\mathrm{e}^{-(n+1) x}}{\mathrm{e}^{-n x}}$
    =$\displaystyle \lim_{n\to\infty}\frac{n^n}{\left(n+1\right)^n}\cdot\frac{\mathrm{e}^{-(n+1)x}}{\mathrm{e}^{-nx}}$=$\displaystyle \mathrm{e}^{-x}\lim_{n\to\infty}\frac{n^n}{\left(n+1\right)^n}$
    • 进一步简化得 $\displaystyle e^{-x} \lim_{n \to \infty} \frac{1}{(1+\frac{1}{n})^n}$。
    • 由$\displaystyle \lim_{n\to\infty}\left(1+\frac1n\right)^n=\mathrm{e}$最终得 $e^{-1-x}$。

• 第二步: 求 $a$ 的值。 根据 $e^{-1-x}<1=\mathrm{e}^0$时收敛

  • $-1-x<0$，得 $x > -1$
  • 综合得 $a = -1$。

(15)

数一2022
已知矩阵 $\boldsymbol{A}$ 和 $\boldsymbol{E}-\boldsymbol{A}$ 可逆, 其中 $\boldsymbol{E}$ 为单位矩阵, 若矩阵 $\boldsymbol{B}$ 满足 $\left[\boldsymbol{E}-(\boldsymbol{E}-\boldsymbol{A})^{-1}\right] \boldsymbol{B}=\boldsymbol{A}$, 则 $B-A=$

(15)

已知$\underbrace{矩阵 \boldsymbol{A}和 \boldsymbol{E}-\boldsymbol{A}可逆}_{AA^{-1}=E，(E-A)(E-A)^{-1}=E}$, 其中 $\boldsymbol{E}$ 为单位矩阵, 若矩阵 $\boldsymbol{B}$ 满足 $\underbrace{\left[\boldsymbol{E}-(\boldsymbol{E}-\boldsymbol{A})^{-1}\right] \boldsymbol{B}=\boldsymbol{A}}_{用AA^{-1}=E破解逆}$, 则 $B-A=$

李艳芳版

• 尝试把逆矩阵$(E-A)^{-1}$消去：
  $\displaystyle \begin{aligned} (E-A)\left[E-(E-A)^{-1}\right] B=(E-A) A \end{aligned}$
  • $\displaystyle \begin{aligned}\xrightarrow[]{打开括号} (E-A-E) B=(E-A) A \end{aligned}$
  • $\displaystyle \begin{aligned} \xrightarrow[]{E-A-E=A}-A B=A-A^2 \end{aligned}\xrightarrow[A是可逆的，尝试把A消去]{左乘A^{-1} }\begin{aligned} -B=E-A \end{aligned}$
    • $\displaystyle \begin{aligned} \xrightarrow[]{移项}B-A=-E . \end{aligned}$

欧几里得版

• 分析题目和等式 $\left[\boldsymbol{E}-(\boldsymbol{E}-\boldsymbol{A})^{-1}\right] \boldsymbol{B}=\boldsymbol{A}$。

• 两边同时左乘 $(\boldsymbol{E}-\boldsymbol{A})$。

  • 得到 $(\boldsymbol{E}-\boldsymbol{A})\left[\boldsymbol{E}-(\boldsymbol{E}-\boldsymbol{A})^{-1}\right] \boldsymbol{B}=(\boldsymbol{E}-\boldsymbol{A}) \boldsymbol{A}$

• 展开并简化等式

  • $[(\boldsymbol{E}-\boldsymbol{A})-\boldsymbol{E}] \boldsymbol{B}=(\boldsymbol{E}-\boldsymbol{A}) \boldsymbol{A}$
  • 得到 $-\boldsymbol{A}\boldsymbol{B}=\boldsymbol{A}-\boldsymbol{A}^2$

• 由于 $\boldsymbol{A}$ 可逆，两边同时左乘 $\boldsymbol{A}^{-1}$

• $-\boldsymbol{A}^{-1} ·\boldsymbol{A} \boldsymbol{B}=\boldsymbol{A}^{-1} ·(\boldsymbol{A}- \boldsymbol{A}^2)$

  • 得到 $-\boldsymbol{B}=\boldsymbol{E}-\boldsymbol{A}$。

• 移项得到 $\boldsymbol{B}-\boldsymbol{A}$ 的值。

  • 得到 $\boldsymbol{B}-\boldsymbol{A}=-\boldsymbol{E}$
    答案 $-\boldsymbol{E}$.

(16)

数一2022
设 $A, B, C$ 为随机事件, 且 $A$ 与 $B$ 互不相容, $A$ 与 $C$ 互不相容, $B$ 与 $C$ 相互独立, $P(A)=$ $P(B)=P(C)=\frac{1}{3}$, 则 $P(B \cup C \mid A \cup B \cup C)=$

(16)

数一2022
设 $A, B, C$ 为随机事件, 且 $A$ 与 $B$ $\underbrace{互不相容}_{P(A \cap B) = 0}$, $A$ 与 $C$ $\underbrace{互不相容}_{P(A \cap C) = 0}$, $B$ 与 $C$ $\underbrace{相互独立}_{P(B \cap C) = P(B) \cdot P(C)}$, $P(A)=$ $P(B)=P(C)=\frac{1}{3}$, 则 $\underbrace{P(B \cup C \mid A \cup B \cup C)=}_{条件概率公式}$

答 应填 $\frac{5}{8}$.
解 由题设, 知 $P(A B)=0, P(A C)=0, P(B C)=P(B) \cdot P(C)$, 则

• $\displaystyle \begin{aligned} P(B \cup C \mid A \cup B \cup C) & =\frac{P((B \cup C) \cap(A \cup B \cup C))}{P(A \cup B \cup C)}=\frac{P(B \cup C)}{P(A \cup B \cup C)} \end{aligned}$

  • $\displaystyle \begin{aligned} =\frac{P(B)+P(C)-P(B C)}{P(A)+P(B)+P(C)-P(A B)-P(A C)-P(B C)+P(A B C)} \end{aligned}$
  • $\displaystyle \begin{aligned} =\frac{\frac{1}{3}+\frac{1}{3}-\frac{1}{9}}{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}-0-0-\frac{1}{9}+0} \end{aligned}$
  • $\displaystyle \begin{aligned} =\frac{\frac{2}{3}-\frac{1}{9}}{1-\frac{1}{9}}=\frac{\frac{5}{9}}{\frac{8}{9}}=\frac{5}{8} . \end{aligned}$

• 第一步：分析题目条件

  • $A$ 与 $B$ 互不相容意味着 $P(A \cap B) = 0$。
  • $A$ 与 $C$ 互不相容意味着 $P(A \cap C) = 0$。
  • $B$ 与 $C$ 相互独立意味着 $P(B \cap C) = P(B) \cdot P(C)＝\frac{1}{9}$。

• 使用条件概率公式，$P(B \cup C \mid A \cup B \cup C) = \frac{P(B \cup C)}{P(A \cup B \cup C)}$。

  • 计算 $P(B \cup C)$
    • 使用概率的加法规则，$P(B \cup C) = P(B) + P(C) - P(B \cap C)$。
    • 代入已知值，得到 $P(B \cup C) = \frac{1}{3} + \frac{1}{3} - \frac{1}{9} = \frac{5}{9}$。
  • 计算 $P(A \cup B \cup C)$
    • 使用概率的加法规则，$P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)$。
    • 由于 $A$ 与 $B$、$A$ 与 $C$ 互不相容，$P(A \cap B \cap C) = 0$。
    • 代入已知值，得到 $P(A \cup B \cup C) = \frac{1}{3} + \frac{1}{3} + \frac{1}{3} - 0 - 0 - \frac{1}{9} + 0 = \frac{8}{9}$。
  • 代入前面计算的值，得到 $P(B \cup C \mid A \cup B \cup C) = \frac{\frac{5}{9}}{\frac{8}{9}} = \frac{5}{8}$

(17)

数一2022
(本题满分 10 分)
设函数 $y(x)$ 是微分方程 $y^{\prime}+\frac{1}{2 \sqrt{x}} y=2+\sqrt{x}$ 的满足条件 $y(1)=3$ 的解, 求 曲线 $y=y(x)$ 的渐近线.

答案 $y=2 x$ 是曲线 $y=2 x+\mathrm{e}^{1-\sqrt{x}}$ 的斜渐近线, 也是唯一的渐近线.

(17)

数一2022
设函数 $y(x)$ 是微分方程 $\displaystyle \underbrace{y^{\prime}+\frac{1}{2 \sqrt{x}} y=2+\sqrt{x}}_{\left\{\begin{array}{l} 一阶线性y^{\prime}+p y=Q(x)，\\y=\mathrm{e}^{-\int p(x) \mathrm{d} x}\left[\int Q(x) \mathrm{e}^{\int p(x) \mathrm{d} x} \mathrm{~d} x+C\right] . \end{array}\right.}$ 的满足条件 $\underbrace{y(1)=3}_{x=1，y=3，初值条件}$ 的解, 求 曲线 $y=y(x)$ 的$\underbrace{渐近线}_{铅直，水平，斜}$.

• 求微分方程 $y^{\prime}+\frac{1}{2 \sqrt{x}} y=2+\sqrt{x}$的通解，$P=\frac{1}{2 \sqrt{x}}, Q=2+\sqrt{x}$

• 由一阶线性微分方程$\displaystyle y(x) =\mathrm{e}^{-\int \frac{1}{2 \sqrt{x}} \mathrm{~d} x}\left[\int \mathrm{e}^{\int \frac{1}{2 \sqrt{x}} \mathrm{~d} x}(2+\sqrt{x}) \mathrm{d} x+C\right]$

  • 计算积分因子 $\displaystyle \mathrm{e}^{-\int \frac{1}{2 \sqrt{x}} \mathrm{~d} x}$=$\mathrm{e}^{-\sqrt{x}}$
  • 将积分因子代入，得$\displaystyle y(x) = \mathrm{e}^{-\sqrt{x}}\left[\int \mathrm{e}^{\sqrt{x}}(2+\sqrt{x}) \mathrm{d} x+C\right]$
    • 拆出 $\displaystyle \int \mathrm{e}^{\sqrt{x}}(2+\sqrt{x}) \mathrm{d} x$,换元令 $\sqrt{x}=u$，$(x)^{\prime}=\left(u^2\right)^{\prime}$ 即 $d x=2 u d u$
    • 积分转换为$\displaystyle \int e^u(2+u) \cdot 2 u d u$
      = $\displaystyle 2 \int \mathrm{e}^u(2u+u^2) \mathrm{d} u$
      $\displaystyle \xlongequal[]{加号拆开}2 \int u^2 \mathrm{e}^u \mathrm{d} u$ + $\displaystyle 2 \int 2u \mathrm{e}^u \mathrm{d} u$
      $\displaystyle \xlongequal[]{对第一项分布}2\left(u^2 \mathrm{e}^u-\int \mathrm{e}^u \cdot 2 u \mathrm{~d} u+\int 2 u \mathrm{e}^u \mathrm{~d} u\right)$
      =$2u^2\mathrm{e}^u$
    • 回代$\sqrt{x}=u$得 $2x\mathrm{e}^{\sqrt{x}}$。

• 得到 $y(x) =\mathrm{e}^{-\sqrt{x}}\left(2 x \mathrm{e}^{\sqrt{x}}+C\right)= 2x + C\mathrm{e}^{-\sqrt{x}}$

• 代入初始条件 $y(1)=3$ 解出 $C$。

  • 由$3=1 \times 2+C \cdot e^{-1}$得到 $C = \mathrm{e}$。
  • 得到具体解 $y(x) = 2x + \mathrm{e}^{1-\sqrt{x}}$。

• 求出曲线的渐近线。

  • 没有铅直渐近线，因为没有无定义点。
  • 计算水平渐近线，发现不存在$\displaystyle \lim _{x \rightarrow+\infty} y(x)=\lim _{x \rightarrow+\infty}\left(2 x+\mathrm{e}^{1-\sqrt{x}}\right)=+\infty \text {, }$。

• 计算斜渐近线：

  • 求斜率 $\displaystyle k=\lim _{x \rightarrow+\infty} \frac{y(x)}{x}\lim _{x \rightarrow+\infty}\left(2+\frac{\mathrm{e}^{1-\sqrt{x}}}{x}\right)\xlongequal[]{\frac{e^{-\infty}}{\infty}=0}2$。
  • 求截距 $\displaystyle b =\lim_{x \to \infty} [y(x) - kx]\xlongequal[]{k=2}\lim _{x \rightarrow+\infty}\left(2 x+\mathrm{e}^{1-\sqrt{x}}-2 x\right)\xlongequal[]{2x-2x=0}\lim _{x \rightarrow+\infty} \mathrm{e}^{1-\sqrt{x}} \xlongequal[]{e^{-\infty}=0} 0$。
  • 得出 $y = 2x$ 是唯一的渐近线。

(18)

数一2022
(本题满分 12 分)
已知平面区域 $D=\left\{(x, y) \mid y-2 \leqslant x \leqslant \sqrt{4-y^{2}}, 0 \leqslant y \leqslant 2\right\}$, 计算 $I=\iint_{D} \frac{(x-y)^{2}}{x^{2}+y^{2}} \mathrm{~d} x \mathrm{~d} y$.

(18)

已知平面区域 $\underbrace{D=\left\{(x, y) \mid y-2 \leqslant x \leqslant \sqrt{4-y^{2}}, 0 \leqslant y \leqslant 2\right\}}_{画图}$, 计算 $\displaystyle I\underbrace{=\iint_{D} \frac{(x-y)^{2}}{x^{2}+y^{2}} \mathrm{~d} x \mathrm{~d} y}_{\left\{\begin{array}{l} 限内画条线，转为极坐标 \\ x=rcost \\y=rsint\\x^2+y^2=r^2\end{array}\right.}$.

• 分析积分区域 $D$ 并画出图形。
  )

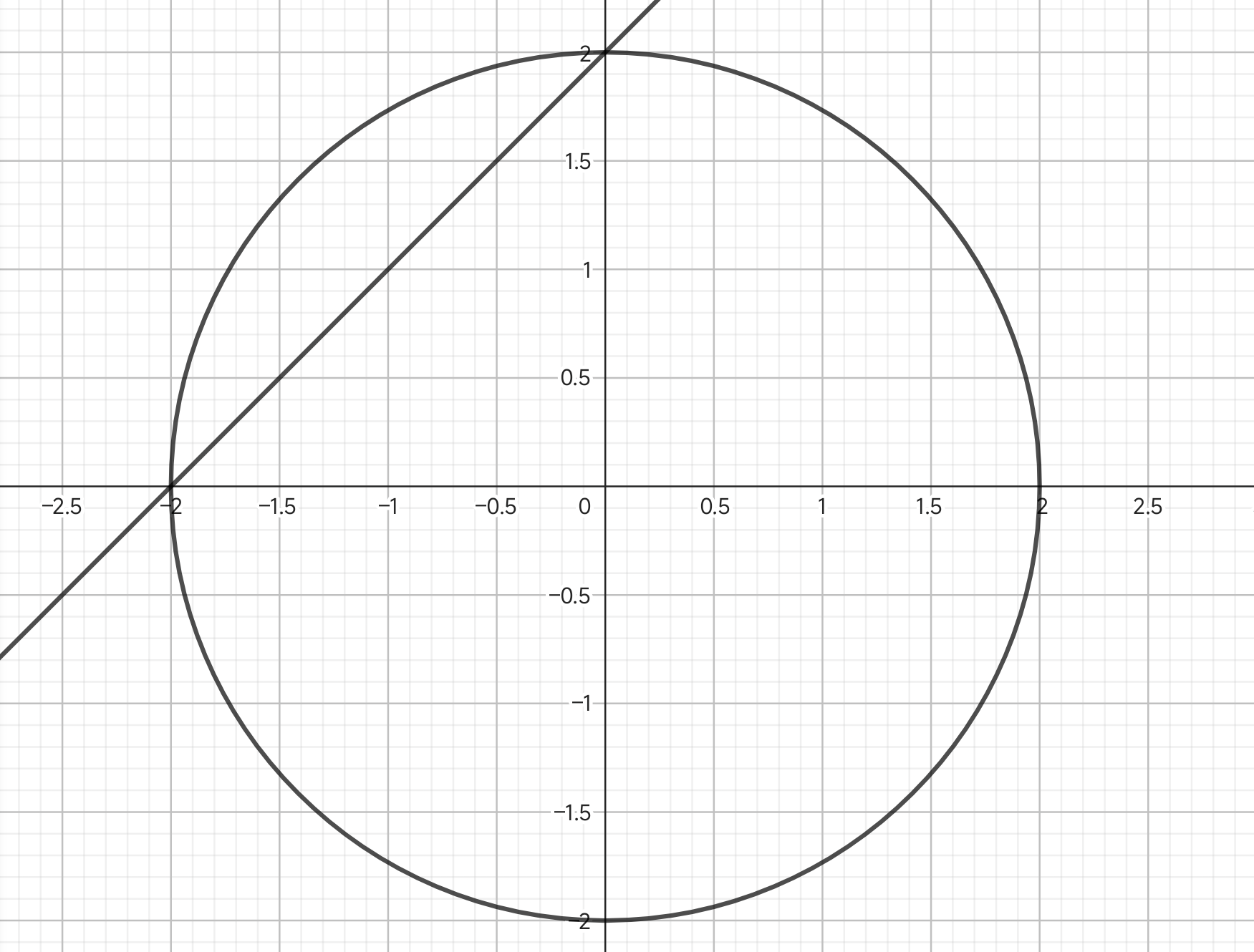• 确定 $D$ 由 $y-2 \leqslant x \leqslant \sqrt{4-y^{2}}, 0 \leqslant y \leqslant 2$ 描述。

  • 将 $D$ 分为 $D_1$ 和 $D_2$。
    • $D_1$: $0 \leqslant r \leqslant 2, 0 \leqslant \theta \leqslant \frac{\pi}{2}$。
    • $D_2$: $0 \leqslant r \leqslant \frac{2}{\sin \theta - \cos \theta}, \frac{\pi}{2} \leqslant \theta \leqslant \pi$。

• 转换到极坐标系下计算二重积分 $I$。

• 极坐标转换：$x = r \cos \theta, y = r \sin \theta, \mathrm{d}x \mathrm{d}y = r \mathrm{d}r \mathrm{d}\theta$。

• 积分表达式：$\displaystyle \begin{aligned} I=\iint_D \frac{(x-y)^2}{x^2+y^2} \mathrm{~d} x \mathrm{~d} y \xlongequal[\begin{array}{l}x^2+y^2=r^2\\dx dy=rdrd\theta\end{array}]{\begin{array}{l}x=r\cos\theta,\\y=r\sin\theta \end{array}} \iint_D \frac{[r(\cos \theta-\sin \theta)]^2}{r^2} \cdot r \mathrm{~d} r \mathrm{~d} \theta\end{aligned}\xlongequal[]{分子分母消去r^2}\iint_D(\cos \theta - \sin \theta)^2 r \mathrm{d}r \mathrm{d}\theta$

• 计算 $D_1$ 和 $D_2$ 上的积分$\displaystyle \begin{aligned}\int_0^{\frac{\pi}{2}}(\cos \theta-\sin \theta)^2 \mathrm{~d} \theta \int_0^2 r \mathrm{~d} r \quad+\int_{\frac{\pi}{2}}^\pi(\cos \theta-\sin \theta)^2 \mathrm{~d} \theta \int_0^{\frac{2}{\sin \theta-\cos \theta}} r \mathrm{~d} r \end{aligned}$

• $D_1$ 积分计算：

  • $\displaystyle \int_0^{\frac{\pi}{2}}(1 - 2 \sin \theta \cos \theta) \mathrm{d}\theta \int_0^2 r \mathrm{d}r\xlongequal[]{计算dr}\left.\int_0^{\frac{\pi}{2}}(1-2 \sin \theta \cos \theta) \mathrm{d} \theta \cdot \frac{1}{2} r^2\right|_0 ^2$
    • $\left.\frac{1}{2} r^2\right|_0 ^2=\frac{1}{2}(4-0)=2$
    • 原式$\displaystyle =2\left(\frac{\pi}{2}-\int_0^{\frac{\pi}{2}} \sin 2 \theta \mathrm{d} \theta\right)\xlongequal[]{凑微分}2\left[\frac{\pi}{2}-\frac{1}{2} \int_0^{\frac{\pi}{2}} \sin 2 \theta \mathrm{d}(2 \theta)\right]$=$2\left(\frac{\pi}{2}-\frac{1}{2} \cdot 2\right)$
    • \displaystyle \begin{align*}\int_0^{\frac{\pi}{2}} \sin 2 \theta \mathrm{d}(2 \theta) \stackrel{\text { 令 } 2 \theta=u}{=} \int_0^\pi \sin u \mathrm{~d} u=-\left.\cos \theta\right|_0 ^\pi=-(-1-1)=2 \text {. }\end{align*}

• $D_2$ 积分计算：

  • $\displaystyle \int_{\frac{\pi}{2}}^\pi(\cos \theta - \sin \theta)^2 \mathrm{d}\theta \int_0^{\frac{2}{\sin \theta - \cos \theta}} r \mathrm{d}r\xlongequal[]{计算dr}\left.\int_{\frac{\pi}{2}}^\pi(\cos \theta-\sin \theta)^2 \mathrm{~d} \theta \cdot \frac{1}{2} r^2\right|_0 ^{\frac{2}{\sin \theta-\cos \theta}}$
    • $\displaystyle \begin{aligned} \left.\frac{1}{2} r^2\right|_0 ^{\frac{2}{\sin \theta-\cos \theta}}\xlongequal[]{代入上下限}\frac{1}{2}\left[\frac{4}{(\sin \theta-\cos \theta)^2}-0\right] =\frac{2}{(\sin \theta-\cos \theta)^2} . \end{aligned}$
    • 原式=$\displaystyle \int_{\frac{\pi}{2}}^\pi(\cos \theta-\sin \theta)^2 \frac{2}{(\sin \theta-\cos \theta)^2} \mathrm{~d} \theta=\int_{\frac{\pi}{2}}^\pi 2 \mathrm{~d} \theta=2 \cdot \frac{\pi}{2}$

• 最终计算 $I$。

  • $I =2\left(\frac{\pi}{2}-\frac{1}{2} \cdot 2\right)+2 \cdot \frac{\pi}{2}=\pi - 2 + \pi = 2\pi - 2$。

• 综上，积分 $I = \iint_{D} \frac{(x-y)^{2}}{x^{2}+y^{2}} \mathrm{d}x \mathrm{d}y = 2\pi - 2$。

(19)

数一2022
(本题满分 12 分)
已知曲线 $L$ 是曲面 $\displaystyle \Sigma: 4 x^{2}+y^{2}+z^{2}=1, x \geqslant 0, y \geqslant 0, z \geqslant 0$ 的边界, 曲面 $\displaystyle \Sigma$ 方向朝上, 曲线 $L$ 的方向和曲面 $\displaystyle \Sigma$ 的方向符合右手法则 计算 $I=\oint_{L}\left(y z^{2}-\cos z\right) \mathrm{d} x+2 x z^{2} \mathrm{~d} y+(2 x y z+x \sin z) \mathrm{d} z$

(19)

已知曲线 $L$ 是曲面 $\displaystyle \underbrace{\Sigma: 4 x^{2}+y^{2}+z^{2}=1, x \geqslant 0, y \geqslant 0, z \geqslant 0}_{画图，补面}$ 的边界,
$\displaystyle \underbrace{曲面 \Sigma方向朝上, 曲线 L的方向和曲面 \Sigma的方向符合右手法则}_{右手法则，先斯托克斯，再用高斯}$
计算 $\displaystyle \underbrace{I=\oint_{L}\left(y z^{2}-\cos z\right) \mathrm{d} x+2 x z^{2} \mathrm{~d} y+(2 x y z+x \sin z) \mathrm{d} z}_{Pdx+Qdy+Rdz=\left|\begin{array}{ccc}d y d z & d x d z & d x d y \\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\P & Q & R\end{array}\right|}$

• )
  • 如果不可偏导，则不能用斯托克斯

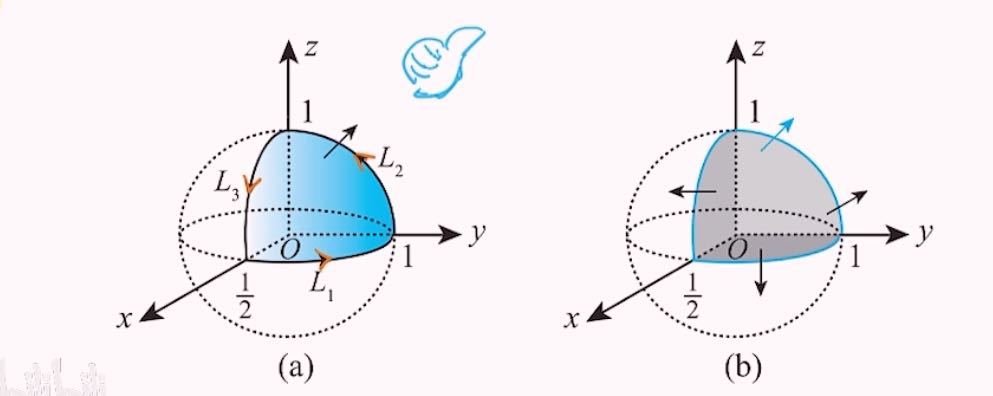不用斯托克斯

• 如图 (a) 所示, 记 $L_1, L_2, L_3$ 分别为 $L$ 在 $x O y$ 面, $y O z$ 面, $z O x$ 面的部分.
  • 在 $L_1$ 上, $\displaystyle z=0, \int_{L_1} \mathrm{~d} z=0$. 起点为 $\left(\frac{1}{2}, 0,0\right)$, 终点为 $(0,1,0)$.
  • 在 $L_2$ 上, $\displaystyle x=0, \int_{L_2} \mathrm{~d} x=0$. 起点为 $(0,1,0)$, 终点为 $(0,0,1)$.
  • 在 $L_3$ 上, $\displaystyle y=0, \int_{L_3} \mathrm{~d} y=0$. 起点为 $(0,0,1)$, 终点为 $\left(\frac{1}{2}, 0,0\right)$.
• $\displaystyle \begin{aligned} I & =\oint_L\left(y z^2-\cos z\right) \mathrm{d} x+2 x z^2 \mathrm{~d} y+(2 x y z+x \sin z) \mathrm{d} z \end{aligned}$
• $\displaystyle \begin{aligned} \xlongequal[将x=0代入L_2，将y=0代入L_3]{将z=0代入L_1}\int_{L_1}\underbrace{(-\cos 0)}_{=-1} \mathrm{d} x+0+\int_{L_3}\underbrace{(-\cos z) \mathrm{d} x+x \sin z \mathrm{~d} z}_{(-x \cos z)=-\cos z+x \sin z} \end{aligned}$
• $\displaystyle \begin{aligned} \xlongequal[]{}(-1) \times\left(0-\frac{1}{2}\right)+\int_{L_3} \mathrm{~d}(-x \cos z)=\frac{1}{2}+\left.(-x \cos z)\right|_{(0,0,1)} ^{\left(\frac{1}{2}, 0,0\right)} \end{aligned}$
• $\displaystyle \begin{aligned} =\frac{1}{2}-\frac{1}{2}=0 . \end{aligned}$

用斯托克斯

• 区别

  • 一型线：ds
  • 二型线：dx+dy(格林)
  • 一型面：dS
  • 二型面：dxdy+dydz+dzdx(高斯)
  • 空间线：dx+dy+dz，用完斯托克斯后用高斯

• 使用方法的判断:由是对空间曲线积分,并且使用右手准则,因此推测用斯托克斯公式

  • 因曲线的正向与曲面的正法向重合，所以用第一种斯托克斯公式
  • 斯托克斯形式1：$\displaystyle \left|\begin{array}{ccc}d y d z & d x d z & d x d y \\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\P & Q & R\end{array}\right|$
  • 斯托克斯形式2：$\displaystyle \left|\begin{array}{ccc}\cos \alpha & \cos \beta & \cos \gamma \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ p & Q & R\end{array}\right| \cdot d S$

• 使用斯托克斯公式将第二型曲线积分转换为第二型曲面积分
  ＝$\displaystyle \left|\begin{array}{lll}d y d z & d z d x & d x d y \\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\y z^2-\cos z & 2 x z^2 & 2 x y z+x \sin z\end{array}\right|$
  按照第一行展开（二阶行列式的计算：主对角线减负对角线＝
  $\displaystyle \iint_{\Sigma}(2xz-4xz) \mathrm{d}y \mathrm{d}z + (-1)(2yz+\sin z - 2yz - \sin z) \mathrm{d}z \mathrm{d}x + (2z^2 - z^2) \mathrm{d}x \mathrm{d}y$

  • $\displaystyle \iint_{\Sigma}(-2xz) \mathrm{d}y \mathrm{d}z + z^2 \mathrm{d}x \mathrm{d}y$

• 曲面不封闭，用高斯补面：添加辅助平面 ，三个面都指向外侧

  • 平面 $\displaystyle \Sigma_1: 令z=0\left(4 x^2+y^2 \leqslant 1\right)$, 取下侧
  • 平面$\displaystyle \Sigma_2: 令x=0\left(y^2+z^2 \leqslant 1\right)$, 取后侧
  • 平面$\displaystyle \Sigma_3: 令y=0\left(4 x^2+z^2 \leqslant 1\right)$, 取左侧

• 计算整个封闭曲面的积分：
  $\displaystyle \iint_{\Sigma+\Sigma_1+\Sigma_2+\Sigma_3}(-2xz) \mathrm{d}y \mathrm{d}z + z^2 \mathrm{d}x \mathrm{d}y =\iint \frac{\partial P}{\partial x}+\frac{\partial R}{\partial z} d V= \iiint_{\Omega}(-2z + 2z) \mathrm{d}v = 0$

• 计算补的面上的积分

  • 计算$\displaystyle \Sigma_1$ 上的积分 ：$z=0$
    • $\displaystyle \iint_{\Sigma_1}(-2 x z) \mathrm{d} y \mathrm{~d} z+z^2 \mathrm{~d} x \mathrm{~d} y=0 .$
  • 计算$\displaystyle \Sigma_2$ 上的积分 ：$x=0$
    • $\displaystyle \iint_{\Sigma_2}(-2 x z) \mathrm{d} y \mathrm{~d} z+z^2 \mathrm{~d} x \mathrm{~d} y=0 .$
  • 计算 $\displaystyle \Sigma_3$ 上的积分： $y=0$
    • $\displaystyle \iint_{\Sigma_3}(-2 x z) \mathrm{d} y \mathrm{~d} z+z^2 \mathrm{~d} x \mathrm{~d} y=0 .$

• 合并计算结果

  • $\displaystyle \begin{aligned} I = \iint_{\Sigma+\Sigma_1+\Sigma_2+\Sigma_3}(-2xz) \mathrm{d}y \mathrm{d}z + z^2 \mathrm{d}x \mathrm{d}y - \iint_{\Sigma_1+\Sigma_2+\Sigma_3}(-2xz) \mathrm{d}y \mathrm{d}z + z^2 \mathrm{d}x \mathrm{d}y \end{aligned}$
  • $\displaystyle \begin{aligned} \xlongequal[]{三个面的积分都是0} 0 -0-0 -0 = 0 \end{aligned}$
  • 因此，积分 $I$ 的值为 0

(20)

数一2022
(本题满分 12 分)
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上有二阶连续导数, 证明: $f^{\prime \prime}(x) \geqslant 0$ 的充分必要条件是对任意不同的实数 $a, b$, 都有 $\displaystyle f\left(\frac{a+b}{2}\right) \leqslant \frac{1}{b-a} \int_{a}^{b} f(x) \mathrm{d} x$ 成立.

(20)

数一2022

1. 理解逻辑关系 $p$ 和 $q$。

• $p$：$f^{\prime \prime}(x) \geqslant 0$。
• $q$：对任意不同实数 $a, b$，有 $\displaystyle f\left(\frac{a+b}{2}\right) \leqslant \frac{1}{b-a} \int_a^b f(x) \mathrm{d}x$。
• 需要证明 $p \Rightarrow q$ (必要性) 和 $q \Rightarrow p$ (充分性)。

2. 证明必要性 $p \Rightarrow q$。

• 使用泰勒公式在 $x = \frac{a+b}{2}$ 处展开 $f(x)$。

  • 展开式：$\displaystyle \begin{aligned}f(x) = f\left(\frac{a+b}{2}\right) + f^{\prime}\left(\frac{a+b}{2}\right)\left(x - \frac{a+b}{2}\right) + \frac{1}{2}f^{\prime \prime}(\xi)\left(x - \frac{a+b}{2}\right)^2\end{aligned}$。
    $\xi$ 介于 $x$ 与 $\frac{a+b}{2}$ 之间
    • 因为$f^{\prime \prime}(x) \geqslant 0$，是整正数，所以$f(x)\geqslant f\left(\frac{a+b}2\right)+f^{\prime}\left(\frac{a+b}2\right)\left(x-\frac{a+b}2\right)$
    • 对不等式两端从 $a$ 到 $b$ 积分。
      • 得到 $\displaystyle \int_a^b f(x) \mathrm{d}x ≥ f\left(\frac{a+b}{2}\right)(b-a) +f^{\prime}\left(\frac{a+b}{2}\right) \int_a^b\left(x-\frac{a+b}{2}\right) \mathrm{d} x$
        • $\displaystyle \int_a^b\left(x-\frac{a+b}{2}\right) \mathrm{d} x \stackrel{\text { 令 } x-\frac{a+b}{2}=t}{=} \int_{-\frac{b-a}{2}}^{\frac{b-a}{2}} t \mathrm{~d} t_{}\xlongequal[]{奇函数}0$
        • 得出 $\displaystyle \int_a^b f(x) \mathrm{d}x \geqslant f\left(\frac{a+b}{2}\right)(b-a)$。

• 移项得出， $\displaystyle f\left(\frac{a+b}{2}\right) \leqslant \frac{1}{b-a} \int_a^b f(x) \mathrm{d}x$。

• 证明充分性 $q \Rightarrow p$。

• 为了证明这个逻辑关系，我们需要采用反证法。我们的目标是证明：如果对任意不同的实数 $a, b$，有 $\displaystyle \int_a^b f(x) \mathrm{d}x \geqslant f\left(\frac{a+b}{2}\right)(b-a)$，则 $f^{\prime \prime}(x) \geqslant 0$。具体步骤如下：

• 假设存在某点 $x_0$ 使得 $f^{\prime \prime}(x_0) < 0$，q也就是$\displaystyle \int_a^b f(x) \mathrm{d}x \geqslant f\left(\frac{a+b}{2}\right)(b-a)$成立

  • 由 $f^{\prime \prime}(x)$ 的连续性可知，存在 $x_0$ 的一个邻域 $[a, b]$ 使得对于任意 $x \in [a, b]$，有 $f^{\prime \prime}(x) < 0$。

• 在区间 $[a, b]$ 上应用泰勒公式展开 $f(x)$。

  • $f(x) = f\left(\frac{a+b}{2}\right) + f^{\prime}\left(\frac{a+b}{2}\right)\left(x - \frac{a+b}{2}\right) + \frac{1}{2} f^{\prime \prime}(\xi)\left(x - \frac{a+b}{2}\right)^2$，其中 $\xi$ 位于 $x$ 和 $\frac{a+b}{2}$ 之间。

• 对 $f(x)$ 从 $a$ 到 $b$ 进行积分。

  • $\displaystyle \int_a^b f(x) \mathrm{d}x = f\left(\frac{a+b}{2}\right)(b-a) + \frac{1}{2} \int_a^b f^{\prime \prime}(\xi)\left(x - \frac{a+b}{2}\right)^2 \mathrm{d}x$。

• 由于 $f^{\prime \prime}(\xi) < 0$，得到积分 $\displaystyle \int_a^b f^{\prime \prime}(\xi)\left(x - \frac{a+b}{2}\right)^2 \mathrm{d}x < 0$。

  • 因此，$\displaystyle \int_a^b f(x) \mathrm{d}x < f\left(\frac{a+b}{2}\right)(b-a)$。
  • 这与题设的条件，当 $f^{\prime \prime}(x_0) < 0$时，$\displaystyle \int_a^b f(x) \mathrm{d}x \geqslant f\left(\frac{a+b}{2}\right)(b-a)$ 矛盾
    • 因此，假设 $f^{\prime \prime}(x_0) < 0$ 不成立。
      综上所述，如果对任意不同的实数 $a, b$，都有 $\displaystyle \int_a^b f(x) \mathrm{d}x \geqslant f\left(\frac{a+b}{2}\right)(b-a)$，则可以推出 $f^{\prime \prime}(x) \geqslant 0$。 综上，$f^{\prime \prime}(x) \geqslant 0$ 是 $\displaystyle f\left(\frac{a+b}{2}\right) \leqslant \frac{1}{b-a} \int_a^b f(x) \mathrm{d}x$ 成立的充分必要条件。

(21)

数一2022
(本题满分 12 分)

• 设二次型 $\displaystyle f\left(x_{1}, x_{2}, x_{3}\right)=\sum_{i=1}^{3} \sum_{j=1}^{3} i j x_{i} x_{j}$.
  (I) 写出 $f\left(x_{1}, x_{2}, x_{3}\right)$ 对应的矩阵;
  (II) 求正交变换 $\boldsymbol{x}=\boldsymbol{Q y}$ 将 $f\left(x_{1}, x_{2}, x_{3}\right)$ 化为标准形;
  (III) 求 $f\left(x_{1}, x_{2}, x_{3}\right)=0$ 的解.
  根据二次型 $f$ 的表达式求对应的矩阵 $\boldsymbol{A}$。
• 分析二次型 $\displaystyle f\left(x_1, x_2, x_3\right)=x^{\top} A x= \sum_{i=1}^{3} \sum_{j=1}^{3} ij x_i x_j$。 $(i, j=1,2,3)$
  • 确定 $\boldsymbol{A}$ 中的元素 $a_{ij} = ij$。
  • 构造矩阵 $\boldsymbol{A}$：
    • $\displaystyle \boldsymbol{A} = \left(\begin{array}{lll}1 \times 1 & 1 \times 2 & 1 \times 3 \\2 \times 1 & 2 \times 2 & 2 \times 3 \\3 \times 1 & 3 \times 2 & 3 \times 3\end{array}\right)=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{array} \right)$
• 求正交变换将 $f\left(x_1, x_2, x_3\right)$ 化为标准形。
• (II) 可以看出 $\boldsymbol{A}$ 是一个秩为 1的矩阵 , 则可推出$\lambda_2=\lambda_3=0$
  • 由于实对称矩阵必能相似对角化,且相似的矩阵具有相同的秩与迹
    • tra(A)=1+4+9=14
  • 则实对称矩阵 $\boldsymbol{A}$ 相似于对角矩阵 $\displaystyle \left(\begin{array}{ccc}14 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right) \cdot$
  • $\boldsymbol{A}$的特征值为 $14,0,0$.
• $\displaystyle (14 E-A) x=0 ，得 14 E-A=\left(\begin{array}{ccc}13 & -2 & -3 \\ -2 & 10 & -6 \\ -3 & -6 & 5\end{array}\right)$
  • $\displaystyle \xrightarrow [抹去第一行]{秩为2，任意一行抹去}\left(\begin{array}{ccc}1 & -5 & 3 \\ -3 & -6 & 5 \\ 0 & 0 & 0\end{array}\right)\xrightarrow{r_2+3 r_1}\left(\begin{array}{ccc}1 & -5 & 3 \\0 & -21 & 14 \\0 & 0 & 0\end{array}\right)$
    • 定 $x_3=3$, 代入2行
      • 由 $-21 \cdot x_2+14 \cdot 3=0$, 得 $x_2=2$
      • 将 $x_3=3, x_2=2$代入第1行
        • 由 $1 \cdot x_1-5 \cdot 2+3 \cdot 3=0$ 得 $x_1=1$
      • 得 $\boldsymbol{\xi}_1 = (1, 2, 3)$。
• 当 $\lambda_2 = \lambda_3 = 0$时， 考虑 $(0 \boldsymbol{E}-\boldsymbol{A}) \boldsymbol{x}=\mathbf{0}$.
  • \displaystyle \begin{align*}-\boldsymbol{(0-A)}=\left(\begin{array}{lll}-1 & -2 & -3 \\-2 & -4 & -6 \\-3 & -6 & -9\end{array}\right) \xlongequal[抹去任意两行]{任意两行成比例，秩为一}\left(\begin{array}{lll}1 & 2 & 3 \\0 & 0 & 0 \\0 & 0 & 0\end{array}\right)\end{align*}
  • 于是, $-\boldsymbol{A} \boldsymbol{x}=\mathbf{0}$ 等价于方程组 $x_1+2 x_2+3 x_3=0$.
• 令$x_2, x_3$为自由元
  • $\displaystyle \left(\begin{array}{l}x_2 \\ x_3\end{array}\right)=\left(\begin{array}{l}1 \\ 0\end{array}\right)$, 可得 $\displaystyle \boldsymbol{\xi}_2=\left(\begin{array}{c}-2 \\ 1 \\ 0\end{array}\right)$
  • $\displaystyle \begin{aligned} \binom{x_2}{x_3}=\binom{0}{1} \end{aligned}$，可得$\displaystyle \boldsymbol{\xi}_3=\left(\begin{array}{c}-3 \\ 0 \\ 1\end{array}\right)$
• 求$\lambda=14$的特征向量：方法2
  • 由方程组 $x_1+2 x_2+3 x_3=0$.
  • 得出
• 将 $\boldsymbol{\xi}_1, \boldsymbol{\xi}_2, \boldsymbol{\xi}_3$ 单位正交化. 实际上, 由于 $\boldsymbol{\xi}_1$ 与 $\boldsymbol{\xi}_2, \boldsymbol{\xi}_3$ 均正交,因为是对称矩阵的不同特征值的特征向量相互垂直。 故正交化的过程只需将 $\boldsymbol{\xi}_2, \boldsymbol{\xi}_3$ 施密特正交化.
• $\displaystyle \begin{aligned} & \boldsymbol{\beta}_1=\boldsymbol{\xi}_1, \end{aligned}$
• $\displaystyle \begin{aligned} \boldsymbol{\beta}_2=\boldsymbol{\xi}_2, \end{aligned}$
• $\displaystyle \begin{aligned} \boldsymbol{\beta}_3=\boldsymbol{\xi}_3-\frac{\left(\boldsymbol{\beta}_2, \boldsymbol{\xi}_3\right)}{\left\|\boldsymbol{\beta}_2\right\|^2} \boldsymbol{\beta}_2=\left(\begin{array}{c}-3 \\0 \\1\end{array}\right)-\frac{6}{5}\left(\begin{array}{c}-2 \\1 \\0\end{array}\right)=\left(\begin{array}{c}-\frac{3}{5} \\-\frac{6}{5} \\1\end{array}\right) . \end{aligned}$
  • 去分母，正交向量长一点，短一点没有关系，因为之后还要单位化
  • 求得 $\boldsymbol{\beta}_2 = (-2, 1, 0), \boldsymbol{\beta}_3 = (-3, -6, 5)$。
• 单位化
  • 将 $\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3$ 单位化, 可得$\displaystyle \boldsymbol{\varepsilon}_1=\frac{\boldsymbol{\beta}_1}{\left\|\boldsymbol{\beta}_1\right\|}=\frac{1}{\sqrt{14}}\left(\begin{array}{l}1 \\2 \\3\end{array}\right), \quad \boldsymbol{\varepsilon}_2=\frac{\boldsymbol{\beta}_2}{\left\|\boldsymbol{\beta}_2\right\|}=\frac{1}{\sqrt{5}}\left(\begin{array}{c}-2 \\1 \\0\end{array}\right), \quad \boldsymbol{\varepsilon}_3=\frac{\boldsymbol{\beta}_3}{\left\|\boldsymbol{\beta}_3\right\|}=\frac{1}{\sqrt{70}}\left(\begin{array}{c}-3 \\-6 \\5\end{array}\right)$
  • 并形成正交矩阵 $\boldsymbol{Q}$
    • 令 $\boldsymbol{Q}=\left(\boldsymbol{\varepsilon}_1, \boldsymbol{\varepsilon}_2, \boldsymbol{\varepsilon}_3\right)$, 可得 $\displaystyle \boldsymbol{Q}^{-1} \boldsymbol{A} \boldsymbol{Q}=\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{Q}=\left(\begin{array}{ccc}14 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right)$,
  • 得到 $f\left(x_1, x_2, x_3\right)$ 的标准形：
    • $f\left(x_1, x_2, x_3\right)$ 化为 $14y_1^2$。

1. 求解 $f\left(x_1, x_2, x_3\right) = 0$。

• $f\left(x_1, x_2, x_3\right) \stackrel{\boldsymbol{x}=\boldsymbol{Q} \boldsymbol{y}}{=} 14 y_1^2=0$. 解出 : $y_1=0$.此时 $y_2, y_3$ 为任意常数.
  • 因此, 所求的通解$x=Qy$为 $\displaystyle \left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right)=\boldsymbol{Q}\left(\begin{array}{c}0 \\ y_2 \\ y_3\end{array}\right)=\left(\boldsymbol{\varepsilon}_1, \boldsymbol{\varepsilon}_2, \boldsymbol{\varepsilon}_3\right)·\left(\begin{array}{c}0 \\ y_2 \\ y_3\end{array}\right)$
    • $\displaystyle \begin{aligned} & =\left(\begin{array}{ccc}\frac{1}{\sqrt{14}} & -\frac{2}{\sqrt{5}} & -\frac{3}{\sqrt{70}} \\\frac{2}{\sqrt{14}} & \frac{1}{\sqrt{5}} & -\frac{6}{\sqrt{70}} \\\frac{3}{\sqrt{14}} & 0 & \frac{5}{\sqrt{70}}\end{array}\right)\left(\begin{array}{c}0 \\y_2 \\y_3\end{array}\right) \end{aligned}$
• $\displaystyle \begin{aligned} =\left(\begin{array}{c}-\frac{2}{\sqrt{5}} y_2-\frac{3}{\sqrt{70}} y_3 \\\frac{1}{\sqrt{5}} y_2-\frac{6}{\sqrt{70}} y_3 \\\frac{5}{\sqrt{70}} y_3\end{array}\right) \end{aligned}$
• $\displaystyle \begin{aligned} \begin{array}{c}\text { 取 } y_2=\sqrt{5} k_1 \\y_3=\sqrt{70} k_2 \end{array}，通解=\left(\begin{array}{c}-2 k_1-3 k_2 \\k_1-6 k_2 \\5 k_2\end{array}\right), k_1, k_2 \text { 为任意常数. } \end{aligned}$

(22)

数一2022
(本题满分 12 分)
设 $X_{1}, X_{2}, \cdots, X_{n}$ 为来自均值为 $\theta$ 的指数分布总体的简单随机样本, $Y_{1}, Y_{2}, \cdots, Y_{m}$ 为来自均值为 $2 \theta$ 的指数分布总体的简单随机样本, 且两样本相互独立, 其中 $\theta(\theta>0)$ 是未知参数.
利用 样本 $X_{1}, X_{2}, \cdots, X_{n}, Y_{1}, Y_{2}, \cdots, Y_{m}$, 求 $\theta$ 的最大似然估计量 $\hat{\theta}$, 并求 $D(\hat{\theta})$.

(22)

设 $X_{1}, X_{2}, \cdots, X_{n}$ 为来自$\displaystyle \underbrace{均值为 \theta 的指数分布总体}_{\left\{\begin{array}{l} f(x)= \begin{cases}\lambda \mathrm{e}^{-\lambda x}, & x>0, \\ 0, & \text { 其他, }\end{cases}\\E(X) =\theta， D(X)=\theta^2\end{array}\right.}$的简单随机样本, $Y_{1}, Y_{2}, \cdots, Y_{m}$ 为来自$\displaystyle \underbrace{均值为 2 \theta的指数分布总体}_{f_Y(y)= \begin{cases}\frac{1}{2 \theta} \mathrm{e}^{-\frac{y}{2 \theta}}, & y>0 \\ 0, & y \leqslant 0 .\end{cases}}$的简单随机样本, 且$\underbrace{两样本相互独立}_{X,Y连乘得似然函数}$, 其中 $\theta(\theta>0)$ 是未知参数.
利用 样本 $X_{1}, X_{2}, \cdots, X_{n}, Y_{1}, Y_{2}, \cdots, Y_{m}$, 求 $\theta$ 的$\underbrace{最大似然估计量}_{会求对数的导数：\ln \theta=\frac{1}{\theta}}$ $\hat{\theta}$, 并求 $\underbrace{D(\hat{\theta})}_{会用性质求方差}$.

• 指数分布
  • 若连续型随机变量 $X$ 的概率密度为$\displaystyle f(x)= \begin{cases}\lambda \mathrm{e}^{-\lambda x}, & x>0, \\ 0, & \text { 其他, }\end{cases}$
  • 其中 $\lambda>0$ 为常数, 则称 $X$ 服从参数为 $\lambda$ 的指数分布.
  • 若 $X$ 服从参数为 $\lambda$ 的指数分布, 则 $E(X)=\frac{1}{\lambda}, D(X)=\frac{1}{\lambda^2}$.
    • 参数和均值互为倒数
• 写出概率密度
  • $X_1, X_2, \cdots, X_n$ ,均值 $E(X)=\theta$, $X$ 的概率密度函数为$\displaystyle f_X(x)= \begin{cases}\frac{1}{\theta} \mathrm{e}^{-\frac{x}{\theta}}, & x>0 \\ 0, & x \leqslant 0\end{cases}$
  • $Y_1, Y_2, \cdots, Y_m$ ,均值$E(Y)=2 \theta$ , $Y$ 的概率密度函数为$\displaystyle f_Y(y)= \begin{cases}\frac{1}{2 \theta} \mathrm{e}^{-\frac{y}{2 \theta}}, & y>0 \\ 0, & y \leqslant 0 .\end{cases}$
• 设 $x_1, x_2, \cdots, x_n, y_1, y_2, \cdots, y_m$ 是相应于样本 $X_1, X_2, \cdots, X_n, Y_1, Y_2, \cdots, Y_m$ 的一组样本值,
  则似然函数为$\displaystyle \begin{aligned} L(\theta)= \begin{cases}\frac{1}{2^m \theta^{m+n}} \mathrm{e}^{-\frac{\sum_{i=1}^n x_i}{\theta}-\frac{\sum_{i=1}^m y_j}{2 \theta}}, & x_i>0, y_j>0, i=1,2, \cdots, n, j=1,2, \cdots, m, \\ 0, & \text { 其他. }\end{cases} \end{aligned}$
• 当 $x_i>0, y_j>0, i=1,2, \cdots, n, j=1,2, \cdots, m$ 时, 取对数得
  $\displaystyle \ln L(\theta)=-m \ln 2-(m+n) \ln \theta-\frac{\sum_{i=1}^n x_i}{\theta}-\frac{\sum_{j=1}^m y_j}{2 \theta} .$
  • 令 $\frac{\mathrm{d}[\ln L(\theta)]}{\mathrm{d} \theta}=0$,
    即 $\displaystyle \xrightarrow[]{\ln \theta=\frac{1}{\theta}}0-\frac{m+n}{\theta}+\frac{\sum_{i=1}^n x_i}{\theta^2}+\frac{\sum_{j=1}^m y_j}{2 \theta^2}=0$,
  • $\displaystyle \begin{aligned} \xrightarrow[]{同乘2\theta^2}-2(m+n) \theta+2 \sum_{i=1}^n x_i+\sum_{j=1}^m y_j=0\end{aligned}$ 解得 $\displaystyle \xrightarrow[]{移项}\theta=\frac{2 \sum_{i=1}^n x_i+\sum_{j=1}^m y_j}{2(m+n)}$.
• 因此, $\theta$ 的最大似然估计量： $\displaystyle \xrightarrow[将y换成Y]{将x换成X}\hat{\theta}=\frac{2 \sum_{i=1}^n X_i+\sum_{j=1}^m Y_j}{2(m+n)}$.
• 下面计算 $D(\hat{\theta})$.
  • 
    $\displaystyle \begin{aligned} D(\hat{\theta}) \xlongequal[]{\hat{\theta}代入}D\left[\frac{2 \sum_{i=1}^n X_i+\sum_{j=1}^m Y_j}{2(m+n)}\right]\xlongequal[]{提出系数}\frac{1}{(m+n)^2} D\left(\sum_{i=1}^n X_i\right)+\frac{1}{4(m+n)^2} D\left(\sum_{j=1}^m Y_j\right) \end{aligned}$
  • $\displaystyle \begin{aligned} \xlongequal[]{提出∑}\frac{1}{(m+n)^2} \sum_{i=1}^n D\left(X_i\right)+\frac{1}{4(m+n)^2} \sum_{j=1}^m D\left(Y_j\right)\end{aligned}$
  • $\displaystyle \begin{aligned} \xlongequal[E(Y)=2 \theta → D(Y)=4 \theta^2]{E(X)=\theta → D(X)=\theta^2}\frac{1}{(m+n)^2}·n· \theta^2+\frac{1}{4(m+n)^2}·m \cdot 4 \theta^2=\frac{\theta^2}{m+n} \end{aligned}$